量子力学
量子力学
sao さんの書込 (2007/10/12(Fri) 11:45)
はじめまして!大学3年生です.量子力学のレポートでわからない問題があったので教えてください!
問題 三次元空間を運動する自由粒子を考える.運動量をp=(Px,Py,Pz),運動エネルギーをEとすると,波動関数ψ(r,t)は ψ(r,t)=exp{i(p*r-Et)/h}=exp{i(PxX+PyY+PzZ-Et)/h} となる. (1)運動エネルギー演算子 p^^2/2m=-h^2*∇^2/2m=-h^2(d^2/dx^2+d^2/dy^2+d^2/dz^2)/2m をψ(r,t)に作用させると運動エネルギーが得られる事を示せ. (2)ψ(r,t)をtで偏微分せよ.その結果を(1)と比較する事により,三次元の自由粒子に対する時間に依存するシュレーディンガー方程式を導け.
※p⇒太文字のp(ベクトル) Px,Py,Pz⇒pのそれぞれの成分 ψ(r,t)⇒rは太文字,tは普通のt h⇒プランク定数h/2π p*r⇒ベクトルpとベクトルrの内積 PxX⇒(pのx成分)×(x) p^^2⇒pハットの2乗 d⇒dはすべてラウンドd
(1)は,p^^2/2mを計算し,ψ*p^2/2mとなり,示せたと思います. (2)が,まったくわかりません.
Re: 量子力学
スパイク さんのレス (2007/10/12(Fri) 13:47)
saoさん,こんにちは.
設問(1)につきましては,大丈夫かと思いますが,一応,
(運動量)演算子 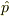 が波動関数
が波動関数 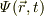 に対し,左側から,右側へ演算しますので,
に対し,左側から,右側へ演算しますので,
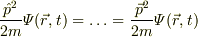
といった形での演繹になるかと思われます.同様であれば,宜しいかと思われます.
設問(2)につきましては,
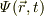 を時間で偏微分すると,波動関数の表式
を時間で偏微分すると,波動関数の表式
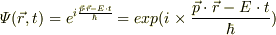
から,
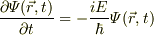
となりますが,
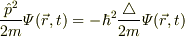
と(1)で示したことから,
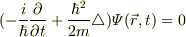
が導出できるかと思われます.まだ,疑問点がありましたら,ご質問ください♪
*)表記上見えにくい箇所の修正を行いました.
Re: 量子力学
sao さんのレス (2007/10/12(Fri) 19:22)
丁寧な解答ありがとうございます!! とても解りやすかったです♪ やってみましたが,最後の導出のところがうまくいきません. そこをもう少し詳しく教えてもらえないでしょうか. お願いします☆
Re: 量子力学
スパイク さんのレス (2007/10/12(Fri) 20:38)
ご評価頂き有難う御座います.後は,どれだけご要望にお答えできるか?
三次元の自由粒子の場合,エネルギーとしては,運動エネルギーだけですので,
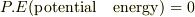
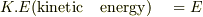
が,成り立ちます.また,演算子記法では,
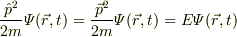
となるわけです.この様にして運動量演算子 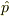 は,運動量保存則により,
は,運動量保存則により,
![[\hat{p},\hat{r}]=i\hbar](http://hooktail.maxwell.jp/bbslog/ba7d294af06dfc2bff42411c43608d6a.png)
となる交換関係を満たす必要(要請)が出てきます.従って運動量演算子 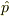 は,
は,
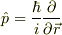
という表式になる事が分かります.一方,演算子の性質(ベクトル演算子の内積はスカラー演算子となる事)から,
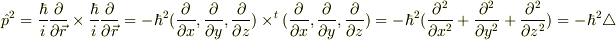
が成り立ちます.即ち,
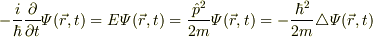
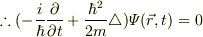
となるわけです♪
Re: 量子力学
sao さんのレス (2007/10/13(Sat) 22:28)
理解できました!!!!! 丁寧に教えてくださって本当にありがとうございます♪ しかし,もう一つ疑問があるのですが… 私の持っている量子力学の教科書を見ると,V(r,t)ψ(r,t)という項が 最後示す式(時間に依存するシュレーディンガー方程式)の左辺に含まれています. V(r,t)ψ(r,t)を式に入れるにはどのように示せはよいのでしょうか?
教科書には下のように書いてあります. …ポテンシャルV(r,t)で表される力を受けて運動する質量mの粒子に対する波動関数ψ(r,t)は,方程式 {-h^2∇^2/2m+V(r,t)}ψ(r,t)=ih(dψ/dt) に従う.これを時間を含むシュレーディンガー方程式という.…
Re: 量子力学
スパイク さんのレス (2007/10/14(Sun) 00:12)
saoさん,お役に立てて幸いかと存じ上げます♪
「理論物理学」(カンパニエーツ)では,
『 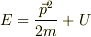 に対応して,次のように置く:
に対応して,次のように置く:
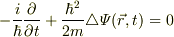

 =一定の場合には,
=一定の場合には, 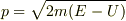 として同様の考えで導出が出来て,
もう一歩進めれば,
として同様の考えで導出が出来て,
もう一歩進めれば,  が変化する場合についても拡張を行うことが出来る.』
といった記述になっております.
が変化する場合についても拡張を行うことが出来る.』
といった記述になっております.
それはさておき,”波動関数が”時間に依存するかどうかという事と,
ポテンシャルは位置(座標)の関数である場合 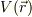 が大半かと思われますので,
まずは,ポテンシャルが時間に依存しない場合について導いてみましょう.
が大半かと思われますので,
まずは,ポテンシャルが時間に依存しない場合について導いてみましょう.
*)(時間変化をしない)中心力や井戸型ポテンシャルは,典型例となります.
<ポテンシャルが時間に依存しない場合>
ポテンシャル 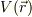 中の波動関数は,
中の波動関数は,
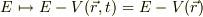 とすることにより,また,
とすることにより,また,
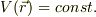 であることから,
であることから,
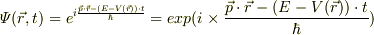
*)波動関数は,簡易的な規格化条件: 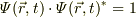 を満たしています.
を満たしています.
と記述できて,
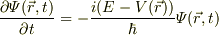
となること,
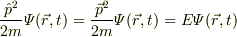
即ち,上記の議論で求めた結果
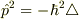
を用いることによって,
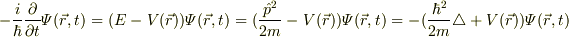
これから,波動関数が時間に依存する 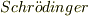 方程式
方程式
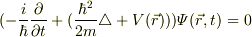
が得られます♪
<ポテンシャルが時間に依存する場合>
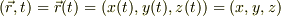
である事と,座標 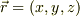 と時間
と時間  の
変数における独立性より,
の
変数における独立性より,
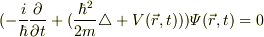
となります♪
#交換関係即ち,時間  ・座標
・座標 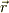 ・運動量
・運動量 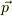 ・エネルギー
・エネルギー  の
#独立性から,ポテンシャルが時間に依存する場合を取り扱うということなのです.
*)それは良かったです♪補足資料を掲示致しました.
の
#独立性から,ポテンシャルが時間に依存する場合を取り扱うということなのです.
*)それは良かったです♪補足資料を掲示致しました.
Re: 量子力学
sao さんのレス (2007/10/14(Sun) 12:14)
ポテンシャルが時間に依存すると,独立性を言わなくてはだめなんですね.そこが私にとっては難しかったですが,なんとなく理解できました!!!
本当に丁寧に教えていただきありがとうございました.スパイクさんのおかげで理解できたので,ちゃんとレポートが書けそうです♪♪ホント感謝です(´∇`) また掲示板を利用させていただく事があると思うので,もし機会があればまたよろしくお願いします☆
![[\hat{p},\vec{r}]=i\hbar \mapsto [\hat{p},\hat{r}]=i\hbar](http://hooktail.maxwell.jp/bbslog/a67aa7e4b83001495750b5219330411d.png)