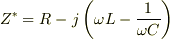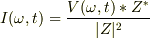電気回路の基本問題
電気回路の基本問題
りんごの木 さんの書込 (2007/10/12(Fri) 02:21)
はじめまして.回路の基本問題なのですが,解に自信がないので質問させてください.
RLC直列回路で電源電圧がV=lVle^(jωt)である. この回路全体に流れる電流Iを求めよ.
インピーダンスZ={(R)^2+(ωL-1/ωc)^2}^(1/2)なので I=lVle^jωt/{(R)^2+(ωL-1/ωc)^2}^(1/2)}と求めました.
eの扱い等(オイラーで展開するとかベクトル表示),がよくわかりません. 解としてこれでよいのでしょうか?
よろしくお願いします.
Re: 電気回路の基本問題
スパイク さんのレス (2007/10/12(Fri) 04:59)
りんごの木さん,おはよう御座います.
>はじめまして.回路の基本問題なのですが,解に自信がないので質問させてください.
なるほど,事情がわかってきました(^^♪
”直流”回路と”交流”回路の違いは,流れに位相(時間)差があることです.
従って,単振動の方程式に見られるように,回路自体に位相  が,入ってきます.その位相(時間)成分を複素表示することにより,定式化したようです(私が本人でないので分かりませんが).従って,
が,入ってきます.その位相(時間)成分を複素表示することにより,定式化したようです(私が本人でないので分かりませんが).従って,
直流回路における表式:
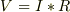
は,位相(時間)を加味した表式:
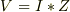
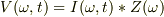
となります.
>RLC直列回路で電源電圧がV=lVle^(jωt)である. >この回路全体に流れる電流Iを求めよ. >インピーダンスZ={(R)^2+(ωL-1/ωc)^2}^(1/2)なので >I=lVle^jωt/{(R)^2+(ωL-1/ωc)^2}^(1/2)}と求めました.
は,いわゆるテクニカルには,間違いないようですね.
>eの扱い等(オイラーで展開するとかベクトル表示),がよくわかりません >解としてこれでよいのでしょうか?
個人的には,ここからが,本題かと思われます.
解の挙動をみる(検証・検算するには)には,まず,図示しないと分かりにくいです.
時間軸を複素数(表示)とするガウス平面・オイラーの公式が必要となります.
実際の数学的な取り扱いとしては,電子回路の計算の際の微分・積分演算を
 の割り算・掛算とする便宜があったようです.
の割り算・掛算とする便宜があったようです.
出来れば,解を適当なソフトでグラフに出力されれば,宜しいかと思われます. (電源電圧の実部を取ってみるなどして解の挙動をみる) #代表的な回路については,定性・定量的に理解するため, #実際に,ブレッドボードなどで,組んでみた方が宜しいかと思います(提案としてですが).
Re: 電気回路の基本問題
yama さんのレス (2007/10/12(Fri) 07:31)
電流を複素数表示する場合は,インピーダンスも複素数で表さないといけません. 複素数表示の電流の実数部分が実際の電流になります.
Re: 電気回路の基本問題
スパイク さんのレス (2007/10/12(Fri) 08:22)
yamaさんおはよう御座います.
りんごの木さん,もし出来れば,複素インピーダンス
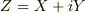
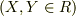
として求めたかどうかを,記述できますでしょうか?
#確かに,下記のyamaさんの複素インピーダンス 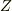 の表式から
#正解を得ることが出来ます(敷居は低くしたかったもので(^^♪
の表式から
#正解を得ることが出来ます(敷居は低くしたかったもので(^^♪
Re: 電気回路の基本問題
yama さんのレス (2007/10/12(Fri) 09:19)
インピーダンスZ={(R)^2+(ωL-1/ωc)^2}^(1/2) として計算されているわけですから,複素インピーダンスは用いなかったということでしょう. 従って計算結果の I=lVle^jωt/{(R)^2+(ωL-1/ωc)^2}^(1/2)} は正しくありません.これでは位相のずれが生じていないことになります.
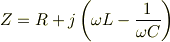
として計算すれば,位相も含めて正しい結果が得られます. この場合
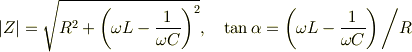
として, 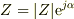 と置くと見通しがよくなると思います.
と置くと見通しがよくなると思います.
Re: 電気回路の基本問題
りんごの木 さんのレス (2007/10/12(Fri) 15:01)
スパイクさんyamaさん,ありがとうございます. 複素インピーダンスはyamaさんが書いてくれたように と求めました.
お2人のアドバイスで 複素インピーダンスZa=R+j{ωL-(1/ωc)} lZl={(R)^2+(ωL-1/ωc)^2}^(1/2) Z=lZl*e^ja a=arctan(ωL-1/ωc)/R
I=V/Z=(lVle^jωt)/(lZle^jωt)=(lVl/lZl)*e^j(ωt-a) =[ lVl/{(R)^2+(ωL-1/ωc)^2}^(1/2)} ]*e^j(ωt-a)
と求められました. スパイクさん,グラフを作成できるサイトを見つけたのでそこで挙動も確認できまた.丁寧な解説ありがとうございました.
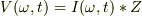 から,
から,
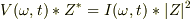
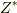 は,複素インピーダンス
は,複素インピーダンス