巷間

Re: 巷間

スパイク さんのレス (2007/09/28(Fri) 01:01)

＃ガロア群は3次対称群の真部分群である．＃

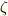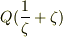複素数解の一つを \zeta とした時， Q(\frac{1}{\zeta}+\zeta) は Qの三次拡大でガロア拡大

三次拡大は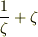， \frac{1}{\zeta}+\zeta の対称性から，導かれます．

従って，「ガロア群は3次対称群の真部分群である．」であることが分かりますので， 宜しくご確認ください．

Re: 巷間

スパイク さんのレス (2007/09/30(Sun) 15:34)

<----■■核心部；何故∃するのか解説願う!■■>

中間体に(?_?)解が存在するのかという点は，方程式の性質を見る上では， 大事だと思います．この手の分析の手法は，解を仮定（というより，置換） することにより（例えば，実数から虚数への解の置換，変数の置換） 性質を探ることが多いようです． ＃因子分析といわれる手法が主流かと思われます． ＃ま，私自身単なる庶民ですし，学者さんによって慣用が違う部分はあるんじゃないでしょうか？ ＃出来ましたら，元方程式を既約部・可約部に分類した上で，次に相関を見たほうがいいと思います（実際的になって来るかと思われます）．

▼唐突に背景

Q[x]/(x^3 + 3*x^2 - 1) | | | Q

を隠匿し

記事No.17985に

>となるので，これから，元と基底を定め，双対基底を定めれば宜しいかと思われます．

と明記していますので，そういった意図はないです．