G さんの書込 (2007/09/26(Wed) 15:09)

http://b4.spline.tv/mynb/?message=105

忙中閑∃の際遊び心でお願い致します．

スパイク さんのレス (2007/09/26(Wed) 22:05)

物理関係の掲示板ですので，若干補足を入れつつ，

まず，

多項式：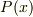

は，因数分解した時に，２次方程式のようには解を持たない（「既約」といいます） 因子が出てきます．これを「中間体」と呼びます．中間体を慣用的に

環：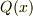

と表記することがあります． 解を持つ因子は，「可約」と呼びまして，多項式を分類したり，性質を調べるために群論を用いる事があります． 一般には，本掲示板には記載がない専門用語や表式，記号が出て来ますので， これを「数学語」と名付けますと，馴染みのある人とない方が居られるかと思われます．

そこで，せっかく実積のある「 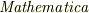」をお持ちのようですので， 議論を物理と数学との”架け橋”として，グラフ（図）の出力をもしされれば， 数式は，「抽象的な何か」と感じても，「グラフ（図）」であれば， イメージ（具現的想起）がし易いのではないかと思われます．

もし宜しければ，Gさんの方でも”一つの枠内に”グラフの方を出力されたり，用語の説明を入れたりして， まとめて行かれれば，皆様に於きましては，より分かりやすいかもしれません．

確かに，三次方程式でも意外と（虚数解を除くことにより），「中間体」等の議論はし易いかもしれません．

数学で言う群論は物理では，慣用的な部分が若干違うことがあるかも判りませんので， 以上宜しくご検討願えれば幸いかと存じ上げます．

＃「利用既約」に準じておられれば返答が得やすいかと思われます． ＃私も 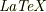は，久しぶりですし，むしろなるべく平易に表現したいかと思っております．

*)2007.9.27表記上の修正を施しました．

スパイク さんのレス (2007/09/27(Thu) 22:45)

追補です．

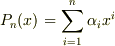において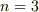， の場合， 与えられた表式

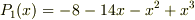
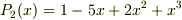
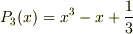
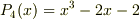
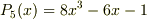
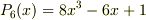
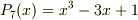
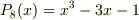
は，可約であることが証明されていますが， 係数行列から，解を一意的に定めることが可能です． ＃これが証明となりますが，宜しければ，ご確認下さい．

一方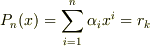， においては， 関数の偶奇性から，係数行列を求め， 収束半径が予め分かっている場合には，三角関数等の周期性関数にて表現することにより， より早く議論が進められたかと思われます． ＃アルゴリズム（論理演算回路）の最適化に通じる部分でもあります．

発展的要素としては，多項式が，多変数の場合ですが，ちょっと考えてみてください．