中間体達　や　解の表現達

Re: 中間体達　や　解の表現達

クロメル さんのレス (2007/09/24(Mon) 06:09)

えーと，解決に至ってませんが（そもそもガロア理論を知りませんので（＾＾；）） 途中経過報告をします．

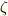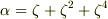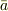\zeta を１の七乗根とし， \alpha=\zeta+\zeta^2+\zeta^4 とします． a に対し， \bar{a} を複素共役とします．

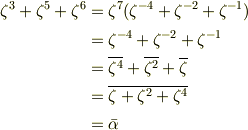
\zeta^3+\zeta^5+\zeta^6 &= \zeta^7(\zeta^{-4}+\zeta^{-2}+\zeta^{-1}) \\&= \zeta^{-4}+\zeta^{-2}+\zeta^{-1} \\&= \overline{\zeta^4}+\overline{\zeta^2}+\overline{\zeta} \\&= \overline{\zeta+\zeta^2+\zeta^4} \\&= \bar{\alpha}

よって，

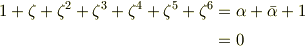
1+\zeta+\zeta^2+\zeta^3+\zeta^4+\zeta^5+\zeta^6 &=\alpha + \bar{\alpha}+1 \\ &= 0

が成り立っています．

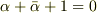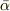ここで， \alpha + \bar{\alpha}+1= 0 をみたすαの性質を考えます． 両辺二乗して，元の式を利用して \bar{\alpha} を消去して変形してやると，

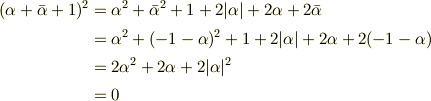
(\alpha + \bar{\alpha}+1)^2 &= \alpha^2+\bar{\alpha}^2+1+2|\alpha|+2\alpha+2\bar{\alpha} \\&= \alpha^2 + (-1-\alpha)^2 + 1 +2|\alpha|+2\alpha+2(-1-\alpha) \\&= 2\alpha^2 +2\alpha + 2|\alpha|^2 \\&= 0

となります．ここで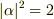， |\alpha|^2=2 となれば，問いの性質を示せることになりま

す．これが実際そうなりますね．

それは，

\alpha \bar{\alpha} &= (\zeta+\zeta^2+\zeta^4)(\bar{\zeta}+\bar{\zeta}^2+\bar{\zeta}^4) \\&=3+2Re[\zeta+\zeta^2+\zeta^3] \\&=2

という風に示せます．

あと，後半は良く分かりませんでしたので，質問させてください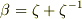． \beta= \zeta+\zeta^{-1} と有りますが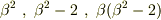， \beta^2 \ , \ \beta^2-2 \ , \ \beta(\beta^2-2) を解とする三次方程式は，どこから出てくるのですか？

Re: 中間体達　や　解の表現達

G さんのレス (2007/09/24(Mon) 10:59)

By computing β^2, β^2 - 2, β(β^2 - 2) とあります．

Re: 中間体達　や　解の表現達

クロメル さんのレス (2007/09/24(Mon) 14:30)

うーん，日本語にすると， β^2, β^2 - 2, β(β^2 - 2)を計算することによって． ということですよね．

Q[x]なる三次多項式は，どこにも書いていない気がします．

Re: 中間体達　や　解の表現達

クロメル さんのレス (2007/09/24(Mon) 15:30)

全然分かりません…．（；A；）

ガロア理論を知らないせいでしょうか？

Re: 中間体達　や　解の表現達

G さんのレス (2007/09/24(Mon) 16:44)

Q[x]なる三次多項式<-----誤読

多項式環Q[x]の３次の元が探しものです.

君は虹（ちゃう２次）をみたか( の検索結果 約 341 件)

多項式環Q[x]のにじの元 も探しものです. 左右草色で視てる筈．

Re: 中間体達　や　解の表現達

スパイク さんのレス (2007/09/24(Mon) 16:48)

参考になるといいんですけど，

>全然分かりません…．（；A；）

ガロア理論は，若干個性的だったような，ええと， キーワードとしては，群論と置換（素数位数の正則巡回群） の中で，可解群に属しているかどうか，判定条件がありますね．

Gさん，これは，中間体に属している場合では？（表題どおりに(-．-)y-゜゜゜

Re: 中間体達　や　解の表現達

G さんのレス (2007/09/24(Mon) 17:43)

http://b4.spline.tv/mynb/?message=98

そのまんま表題

添付体達の図式注視

対応する群達の図式（双対）をも!

Re: 中間体達　や　解の表現達

スパイク さんのレス (2007/09/24(Mon) 18:15)

クロメルさんへ，

Gさんから与えられた表式における，可解かどうかの判定条件（ある程度与えられていますが） をまず，考察されると宜しいかと思われます．

一般には，一次方程式の集合

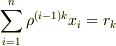
\sum_{i=1}^{n}\rho^{(i-1)k}x_i=r_k

において，可解かどうかの判定条件を（群論により）求めるということなんですけど．

Re: 中間体達　や　解の表現達

クロメル さんのレス (2007/09/24(Mon) 19:01)

むぅ，これは僕の知らないことがいっぱいですね． 僕はこの話の議論にすぐ参加することはできなさそうです．

これはしばらくJohさんの記事にお世話になることになりそうです． どうせ，後期の授業では興味に本意で， 代数と群，体，環の授業を取るつもりなので， この際，勉強してみようかと思います．

いろいろアドバイス，ありがとうございました．

Re: 中間体達　や　解の表現達

G さんのレス (2007/09/24(Mon) 20:50)

http://www.math.nagoya-u.ac.jp/ja/admission/gs/download/exam-mc-2001s-2.pdf

が前半部のHintです．

<-------- すぐ参加することはできmathた（院試で予想し,おそらく解いた問4）

ひき続き御贔屓のほどを

Re: 中間体達　や　解の表現達

スパイク さんのレス (2007/09/24(Mon) 21:16)

>いろいろアドバイス，ありがとうございました．

いえいえ，こちらこそ．物理で知っておくと，役に立ちますよ♪

>ひき続き御贔屓のほどを

実は，クロメルさんの演繹をちょっと見て，ひょっとして”あの”と思いまして．

Gさんのは，良問多いですね(^^♪

Re: 中間体達　や　解の表現達

スパイク さんのレス (2007/09/25(Tue) 00:06)

Gさんへ， 三次の場合は，θによって二次方程式に焼きなおせますね．

Re: 中間体達　や　解の表現達

スパイク さんのレス (2007/09/25(Tue) 13:12)

一応まとめの数式だけ，ご紹介しておきます．

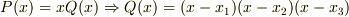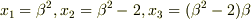
P(x)=xQ(x) \Rightarrow Q(x)=(x-x_1)(x-x_2)(x-x_3) 但し， x_1=\beta^2, x_2=\beta^2 - 2, x_3=(\beta^2 - 2)\beta

即ち，

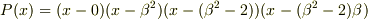
P(x)=(x-0)(x-\beta^2)(x-(\beta^2 - 2))(x-(\beta^2 - 2)\beta)

となるので，これから，元と基底を定め，双対基底を定めれば宜しいかと思われます．

補足：基底と双対基底をグラフに出力すると対称性が明示されると思われます．

おまけ：四則演算と置換で解けますから♪

-以上-