区分求積法について
区分求積法について
yaj さんの書込 (2007/09/21(Fri) 20:03)
お久しぶりです. といっても最終書き込みが何ヶ月も前なので覚えている人はいないと思いますが(笑
現在高2です. 積分の区分求積法について質問です.
区分求積法では,関数f(x)と適当な直線によって囲まれた面積Sを求める方法で,その範囲内の定積分(f(x)>0として)がSに収束することを示しています.
一般的に,この方法を利用して,
円の面積(半径rとすれば)が π 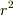 であること
(証明の例→ http://naop.jp/text/3/seki13.html )
や,三角形の面積が(底辺)×(高さ)÷2
であらわせることを証明できます.
であること
(証明の例→ http://naop.jp/text/3/seki13.html )
や,三角形の面積が(底辺)×(高さ)÷2
であらわせることを証明できます.
しかしながら,区分求積法はあくまで定積分がSに「収束」することを示しただけなので,この方法では,円の面積などは,
π 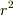 →S
を示しただけで,
π
→S
を示しただけで,
π 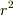 =S
を示していません.
=S
を示していません.
つまり,S=πr~2という公式はいまだに導けていません.
なんかすごい勘違いをしているような気もするのですが,どこがおかしいのかわかっている方がいらしたら,どうかご指摘お願いします.
Re: 区分求積法について
スパイク さんのレス (2007/09/21(Fri) 20:12)
yajさん,こんばんは.
>しかしながら,区分求積法はあくまで定積分がSに「収束」することを示しただけなので,この方法では,円の面積などは, >πr~2→S >を示しただけで, >πr~2=S >を示していません.
区分求積法は,区分された領域の(面)積を求めるためです(目的に対しての方法だということ). つまり,二つのベクトルの内積の値(スカラー)から二つのベクトルを求める事は,一意的に決まらないということなのです.
Re: 区分求積法について
toorisugari no Hiro さんのレス (2007/09/21(Fri) 21:40)
円の面積を区分求積法的に求めるなら,以下の通りです.
「半径  の円を放射状にカットして
の円を放射状にカットして  個のピースに等分割する.各ピースの面積は
個のピースに等分割する.各ピースの面積は  で近似される.
で近似される. 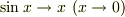 を考慮すると,各ピース
を考慮すると,各ピース  個足しあわせたものの面積は
個足しあわせたものの面積は 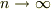 で
で 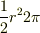 に収束する.つまり円の面積は
に収束する.つまり円の面積は 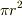 に収束する.」
に収束する.」
「これは本当に面積を求めたことになるのか?」ってことでしょうか?
それに対する回答として以下の考え方があります.
円Cに外接する正n角形 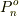 と円Cに内接する正n角形
と円Cに内接する正n角形 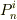 の面積を考える.円Cの面積を
の面積を考える.円Cの面積を 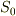 ,外接する正n角形の面積を
,外接する正n角形の面積を 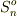 ,内接する正n角形の面積を
,内接する正n角形の面積を 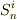 とすれば,
とすれば,
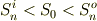
が成り立ちます.
多角形の面積は
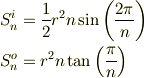
で与えられます.
ここで,「 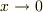 なら
なら 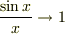 ,
, 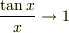 」であることを使うと,
」であることを使うと,
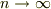 にたいして
にたいして
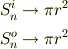
が成り立ちます.
一般に
「 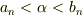 で
で 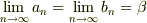 が成り立つのなら,
が成り立つのなら, 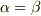 」
」
がいえるので,これにより円の面積 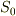 は
は 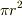 に「等しい」ことが「しめされた」.つまり「公式」が「導けました」.
に「等しい」ことが「しめされた」.つまり「公式」が「導けました」.
....って話ではないのですか?
Re: 区分求積法について
佑弥 さんのレス (2007/09/21(Fri) 21:55)
恐らく,高校までの数学では面積をきちんと定義していなかったのではないで しょうか?感覚的にこういうものだろうという事を使っていたと思います.
それでも,数?で積分を習った時に面積を積分で求める事が出来る事を習った 事と思います.
むしろ,区分求積法によって積分を定義し,面積も定義すると考えた方が良い かも知れません.(もちろん多少問題がありますが...)
というような事に対する疑問だったのでしょうか?
Re: 区分求積法について
zoro さんのレス (2007/09/22(Sat) 15:41)
yajさん,説明ではありませんが...,ちょっと関連する本をご紹介してみます.
私は高校生の頃,「数学は,物理に使う道具」として捉えて,数学をじっくり考えた事がありませんでした.最近,不思議と数学に興味が出て来て,初等的な数学や,物理数学の基本を見直したりしています.
その中でも高校生むけの数学の本として;
数学が育っていく物語(全6冊), 志賀 浩二・著, 岩波書店
・第1週極限の深みーーー 数列と級数 ・第2週解析性ーーー 実数から複素数へ ・第3週積分の世界ーーー 一様収束とフーリエ級数 ・第4週線形性ーーー 有限次元から無限次元へ ・第5週方程式ーーー 解ける鎖,解けない鎖 ・第6週曲面ーーー 硬い面,柔らかい面
を市民図書館で拝見しました.
志賀さんの本は,不思議と数学の癖が少なく,読み手が疑問になりそうな点が,そのすぐ近傍に解説として取り上げられる事が多く,安心して自問しながら読めます.
物理なり,物理数学を進める基礎としての数学をじっくりと身につけるのには好適かも知れません.一度,ご自分の目で確かめられると良いでしょうね.
このシリーズの説明には;
微積分,線形代数,関数論,微分方程式,フーリエ解析,多様体などのテーマを高校2年〜3年生くらいの数学の知識でわかるようにやさしく語ります.
と書かれています.私は,数学専攻の学生さんならいざ知らず,物理専攻の学生さんなら,高校では第3週位,大学の夏休みにその後を読む位で丁度良いかもしれないと感じました.
〜〜〜 ちなみに,私は,高校で積分を習った時に,円周率が直接的に定義出来ると思い込んでいました.幾ら進んでも駄目で,ギャフンでした.
Re: 区分求積法について
yaj さんのレス (2007/09/22(Sat) 16:07)
>これにより円の面積はに「等しい」ことが「しめされた」.つまり「公式」が「導けました」. (数式は省略します..)
とのことですが(これはいわゆる,「はさみうちの原理」ってやつですよね?),これは 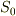 が
(
が
( 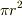 の極限値) ≦
の極限値) ≦ 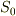 ≦ (
≦ ( 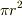 の極限値)
の範囲で存在する
すなわち,
の極限値)
の範囲で存在する
すなわち,  を示しただけで,
を示しただけで,
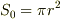 を示したことにはならないと思います.
(
を示したことにはならないと思います.
( 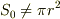 でもこの等式を満たす
でもこの等式を満たす 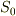 は存在するかも知れません)
は存在するかも知れません)
>むしろ,区分求積法によって積分を定義し,面積も定義すると考えた方が良い かも知れません.(もちろん多少問題がありますが...)
区分求積法ではすでに,その方法の中で,長方形の面積を求める公式が利用されている(つまり面積がすでに定義されている)ので面積は定義できないと思います.
問題がありますね(笑
>恐らく,高校までの数学では面積をきちんと定義していなかったのではないでしょうか? そうなんです..
数学では,面積はどのように定義されているのでしょうか? 色々と調べてみたのですが,厳密な定義が見つかりませんでした. 個人的には,定積分によって得られた「極限値」のような気がします.
>つまり,二つのベクトルの内積の値(スカラー)から二つのベクトルを求める事は,一意的に決まらないということなのです. つまり,面積は,一意的にひとつの値をとることができない(=極限値としてあらわすしかない?)ということでしょうか?
- 勘違いしてたらすみません.
> zoro さん アドバイスありがとうございます. 今度学校の図書館を探ってみます. そして授業中に読みます(笑
Re: 区分求積法について
佑弥 さんのレス (2007/09/22(Sat) 18:12)
面積は,積分によって定義されます.区分求積法によって 定義してはいけないと言うのは,長方形の面積を求める公式 を使ってしまっているからと言うよりも,区分求積法によっ て値が一意に定まる事の証明が高校ではなされていないため です.
そこで,どうするかと言えば,次の記事にかかれているように 積分を定義してしまいます.
//ja.wikipedia.org/wiki/%E7%A9%8D%E5%88%86 (はじめにhttp:を補ってください.)
途中に長方形に面積を使っているかのようにかかれているのですが, これは解りやすく書くための便宜的な物であって,この式で積分を 定義すると言う事に注意してください.
Re: 区分求積法について
toorisugari no Hiro さんのレス (2007/09/22(Sat) 18:44)
> これは 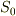 が
>(
が
>( 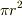 の極限値) ≦
の極限値) ≦ 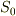 ≦ (
≦ ( 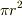 の極限値)
> の範囲で存在する
> すなわち,
の極限値)
> の範囲で存在する
> すなわち,  を示しただけで,
>
を示しただけで,
> 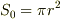 を示したことにはならないと思います.
>(
を示したことにはならないと思います.
>( 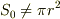 でもこの等式を満たす
でもこの等式を満たす 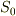 は存在するかも知れません)
は存在するかも知れません)
何か「極限値」を誤解されているようです.
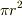 や
や 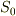 は値であって,さらに極限をとるものではありません.はさみうちの原理で示されるのは
は値であって,さらに極限をとるものではありません.はさみうちの原理で示されるのは
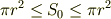
です(なぜ等号が現れるかは難しいところですが).
これは 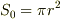 以外の何者でもありません.
以外の何者でもありません.
Re: 区分求積法について
スパイク さんのレス (2007/09/22(Sat) 18:50)
皆さん,こんばんは.
>>つまり,二つのベクトルの内積の値(スカラー)から二つのベクトルを求める事は,一意的に決まらないということなのです. >つまり,面積は,一意的にひとつの値をとることができない(=極限値としてあらわすしかない?)ということでしょうか?
理解は個人差もあることをご理解いただいた上で,
微分・積分においては,必要とされる,無限回の操作を「極限値」として,求める手法がある程度確立しているということ になります.
但し,ご指摘の通り,収束可能な範囲において,値が決まりますから,不確定要因も確かに存在すると言う事です.
Re: 区分求積法について
yaj さんのレス (2007/09/22(Sat) 21:07)
>toorisugari no Hiroさん
すみません,
「のことですが(これはいわゆる,「はさみうちの原理」ってやつですよね?) (中略)(でもこの等式を満たすは存在するかも知れません)」
を訂正します.. 今回の場合は,「はさみうちの原理」のを使う場合とは,多少違うみたいです. (以下訂正)
明らかに,
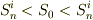 なので(つまり,等号は成り立たちません),
なので(つまり,等号は成り立たちません),
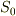 のとりうる範囲は
(
のとりうる範囲は
( 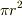 の極限値) <
の極限値) < 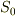 < (
< ( 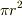 の極限値)
の極限値)
となるので,
 は示しましたが,
は示しましたが, 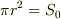 までは示していないと思います.
までは示していないと思います.
>(なぜ等号が現れるかは難しいところですが).
ご指摘のとおり,等号が現れない限り 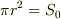 は示せないと思います.
は示せないと思います.
>面積は,積分によって定義されます 要するに,ある範囲内の定積分がある数αに収束した時,その範囲内の面積Sを,S=α と定義するってことですよね?(自信なし)
頭が混乱してきました(笑 馬鹿ですみません..
Re: 区分求積法について
佑弥 さんのレス (2007/09/22(Sat) 22:52)
そうです.細かい事をいいだすとキリがなくなってしまいますが, きちんと定積分が出来れば,ソレで面積を定義すると言う事です.
それで,問題の区分求積法は何を主張しているかと言うと,
関数 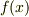 が区間
が区間 ![[0,1]](http://hooktail.maxwell.jp/bbslog/ccfcd347d0bf65dc77afe01a3306a96b.png) で定積分可能な関数とする.
(実際は区間
で定積分可能な関数とする.
(実際は区間 ![[a,b]](http://hooktail.maxwell.jp/bbslog/2c3d331bc98b44e71cb2aae9edadca7e.png) でいいのですが,簡単のため
でいいのですが,簡単のため ![[0,1]](http://hooktail.maxwell.jp/bbslog/ccfcd347d0bf65dc77afe01a3306a96b.png) とします.)
この時,
とします.)
この時,
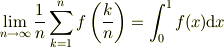
となる.
という事を言っているわけです.
Re: 区分求積法について
toorisugari no Hiro さんのレス (2007/09/23(Sun) 03:16)
> 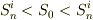 > なので(つまり,等号は成り立たちません),
>
> なので(つまり,等号は成り立たちません),
> 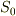 のとりうる範囲は
>(
のとりうる範囲は
>( 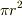 の極限値)<
の極限値)< 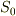 < (
< ( 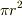 の極限値)
> となるので,
の極限値)
> となるので,
なりません.
( 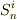 の極限値)
の極限値) 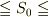 (
( 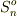 の極限値)
です.等号が含まれるのは「極限値」とは何かを考えれば必然であることがわかります.
の極限値)
です.等号が含まれるのは「極限値」とは何かを考えれば必然であることがわかります.
# 任意の整数  で
で 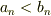 が成り立つなら,
が成り立つなら, 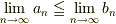 です.
です.
Re: 区分求積法について
yaj さんのレス (2007/09/23(Sun) 08:26)
面積Sの円に内接する正n角形の面積を 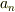 ,外接する正n角形の面積を
,外接する正n角形の面積を 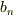 として,nが十分に大きい時,
として,nが十分に大きい時,
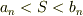 …?
…?
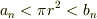 …?
…?
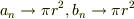 が成り立つはずです.
が成り立つはずです.
ここで明らかに, 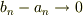 ,
, 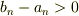 ?を変形すると
?を変形すると
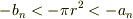 …?'
?+?'は
…?'
?+?'は
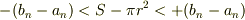
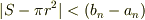 つまり
つまり
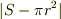 < 0の極限値(正の数)
です.
< 0の極限値(正の数)
です.
ここから,理論的に,どのようにして 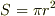 を導くのでしょうか.
を導くのでしょうか.
Re: 区分求積法について
佑弥 さんのレス (2007/09/23(Sun) 08:41)
?が成立する事は証明を要しますが,とりあえず
ここでは認めるとして, 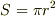 を導きましょう.
を導きましょう.
背理法によって示す事にします. 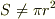 と仮定します.
と仮定します.
このとき,適当な正の数 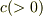 を用いて,
を用いて,
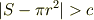
が成り立ちます.
しかし,
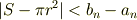
であって,この式の右辺は 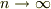 で
で  に収束します.
に収束します.
この上の二つの不等式は両立しませんから,矛盾です.
こんな感じでよいですか?
Re: 区分求積法について
zoro さんのレス (2007/09/23(Sun) 16:23)
yajさん,私は2点に感銘を受けました.
論議を自分の目からみて,納得出来るまで回答者を駆り立てて,最終的に納得されたのが凄いと思います.
もう一つの驚きは,最初は数式表現に,アスキー文字とLaTeX混在だったのが,LaTeXに統一出来た事です.きっと,他の質問のときは,また腕を上げそうで楽しみです.
さて,折角,納得されたのですから,色々と説明を下さった解説者の方々に,yajさんがどのような経路で理解されたかを示す上で,ご自分の好きな回答を書れたら如何かと思います.
きっと,高校生・大学生の方々にも,参考になると思います.
論議の傍観者より.
Re: 区分求積法について
クロメル さんのレス (2007/09/24(Mon) 08:06)
解決されたようで,おめでとうございます.ちょっと気になることがあったので,一言.
区分求積法で定まる値をΣとして,区分をこまかくした極限の収束値がlimΣ=πr^2であり,面積Sに収束することが分かっているならば,単にπr^2=S.という話のようなきがします.
Re: 区分求積法について
yaj さんのレス (2007/09/24(Mon) 09:58)
関数 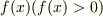 ,
,  軸,
軸,  軸,
軸, 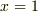 (便宜上このように定義します)に囲まれた範囲の面積
(便宜上このように定義します)に囲まれた範囲の面積  は,
は,
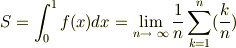
である.
つまり,日本語で表現するならば, 面積Sは,その区間内の定積分によって定義され,その定積分は 区分求積法によって,その範囲内の微小な長方形の総和の極限値に等しいことが示される.
よって,半径rの円の面積Sについて
区分求積法によって出てきた極限値が 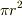 であれば,
であれば,
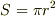 である.(定義する)
である.(定義する)
みたいな感じでしょうか.(まちがってたらすみません)
>区分求積法で定まる値をΣとして,区分をこまかくした極限の収束値がlimΣ=πr^2であり,面積Sに収束することが分かっているならば,単にπr^2=S.という話のようなきがします.
そのとおりなのですが,後から考えて見れば,これはただ純粋に
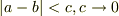 ⇒
⇒ 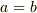 が納得できなかっただけのようです.
が納得できなかっただけのようです.
>納得出来るまで回答者を駆り立てて 納得するまで回答してくださった(しかも恐ろしく迅速に)回答者の方々には本当に感謝しています.本当にありがとうございました.
Re: 区分求積法について
スパイク さんのレス (2007/09/24(Mon) 10:28)
おはよう御座います.
>つまり,日本語で表現するならば, >面積Sは,その区間内の定積分によって定義され,その定積分は 区分求積法によって,その範囲内の微小な長方形の総和の極限値に等しいことが示される.
・・・
>みたいな感じでしょうか.(まちがってたらすみません)
全くその通りです♪ #日本語が抽象的な表現になっていたら申し訳ありません(^^♪
Re: 区分求積法について
zoro さんのレス (2007/09/24(Mon) 10:35)
表現の話で恐縮ですが,
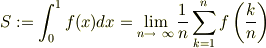
とすると,お腹がスマートに見えます.中高年のある一群の読者はほっとしますよ.
味噌は,「(...)」→「left(...)right」です.
「頭の力」と「指の力」とは同時に磨く必要があるようです.ノート&鉛筆も大切ですが,PCの時代,キーボードで式を表現出来ると,鉛筆に無い利点;
・カット&ペーストで,気楽に式が書けて,間違いも少ない. ・書いた後で判読しがたいギリシャ文字が,明瞭になる! ・文字表現が明瞭な分,「悪い文」を校正する余裕が生まれる.
があります.サイバースペースで,縦横無尽に遊んでくださいませ.
最後に,当たり前の事ですが,
(1)何かに疑問をもつ (2)疑問点をいろんな角度から眺めて,解釈してみる. (3)それでも「判らん部分」を質問してみる. (4)Q&Aで「判らん部分」→「判った部分」に変換出来れば良し. 判らなければ先送りして,時々「振り返ってみる」,そのうち判ったら, (5)「判らん部分」を問題として,自分の言葉で回答を書いてみる.できれば,こちらのような掲示板に回答してみる.その回答に質問が出てくれば,自分の言葉で回答をする.此れが,一番効率の良い勉強方法かも知れませんね.
Re: 区分求積法について
クロメル さんのレス (2007/09/24(Mon) 15:37)
>yajさん
そうでしたか,僕の書いたことはちょっと方向が違うことのようですね. 疑問が解決されたようで,めでたしめでたし.ですね^^