曲率半径，瞬間中心を求めたい

オリーブを愛する者さんの書込 (2007/09/20(Thu) 20:08)

数学を利用して人間の動きを色々と分析したいと思っている者です．

両足で立っている姿勢で右手を前方に上げていくときの人間の動きをビデオカメラで撮影して，指先の移動軌跡を分析したいと思っています．求めたいのは，指先の移動軌跡上の様々な位置における曲率半径，瞬間中心です．ビデオカメラは被験者の側面に置いて撮影しています．被験者を側面から見たとき，手を上げるときの指先は円に近い曲線軌跡を描きます． 1秒間に30コマの指先の2次元座標データが得られているとして，ある一時点での曲率半径や瞬間中心はどのように求めたらよいのでしょうか．

フレネ・セレの公式は使えるのでしょうか．弧長パラメータ表示というのはどうやったらよいのでしょうか．離散的な指先の座標データから，曲線の関数を先に求めないとできないのでしょうか．

質問が多くて申し訳ありませんが，アドバイスをいただければ幸いです．

Re: 曲率半径，瞬間中心を求めたい

toorisugari no Hiro さんのレス (2007/09/20(Thu) 21:44)

曲率半径を求めたいだけですからフレネ・セレの公式( http://www12.plala.or.jp/ksp/vectoranalysis/FrenetFrame/ http://www12.plala.or.jp/ksp/vectoranalysis/FrenetSerret/ http://www12.plala.or.jp/ksp/vectoranalysis/Curvature/ )のフルバージョンは必要ありません．

点 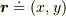$\bm{r}\doteq(x,y)$ のフレーム毎の時系列データ 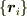$\{\bm{r}_i\}$ があるとします．また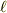， $\ell$ を弧長とします．

変位ベクトル及び切片長の時系列データを

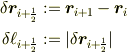
$\delta \bm{r}_{i+\frac{1}{2}} &:= \bm{r}_{i+1}-\bm{r}_{i}\\\delta \ell_{ i+\frac{1}{2}} &:= |\delta \bm{r}_{ i+\frac{1}{2} }|$

で定義します．

次に単位接ベクトル，及び，その変化率を

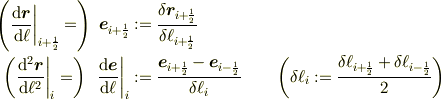
$\left(\left.\frac{\mathrm{d} \bm{r}}{\mathrm{d} \ell} \right|_{i+\frac{1}{2}} =\right)~\bm{e}_{i+\frac{1}{2}} &:= \frac{ \delta \bm{r}_{ i+\frac{1}{2} } }{ \delta \ell_{ i+\frac{1}{2} } }\\\left(\left.\frac{\mathrm{d}^2 \bm{r}}{\mathrm{d} \ell^2} \right|_{i} =\right)~\left.\frac{\mathrm{d} \bm{ e}}{\mathrm{d} \ell}\right|_{i} &:= \frac{\bm{e}_{i+\frac{1}{2}} - \bm{e}_{i-\frac{1}{2}} }{\delta \ell_{i} } \qquad \left(\delta \ell_{i} := \frac{\delta \ell_{ i+\frac{1}{2} } + \delta \ell_{ i-\frac{1}{2} }}{2}\right)$

で計算します．

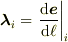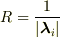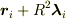こうして得られた $\bm{\lambda}_{i} = \left.\frac{\mathrm{d} \bm{ e}}{\mathrm{d} \ell}\right|_{i}$ を使えば曲率半径 $R=\frac{1}{|\bm{\lambda}_{i}|}$ 瞬間中心 $\bm{r}_{i}+ R^2 \bm{\lambda}_{i}$ が求められます．

以上で形式的には計算ができます．しかし，注意事項があります．

単位接ベクトルやその変化率の計算においては，微分を差分で近似をしてますから，切片長が曲率半径に対して十分小さくとれないと打ち切り誤差が無視できなくなります．

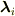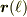また， $\bm{\lambda}_{i}$ は $\bm{r}(\ell)$ の2階微分ですから算出には3点を使っていますが，実際には点の位置に測定誤差があるので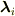， $\bm{\lambda}_{i}$ に対するノイズがひどいと予想されます．ですから，(重み付き)最小二乗法を使って5点以上のデータ 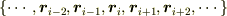$\{\cdots,\bm{r}_{i-2}, \bm{r}_{i-1}, \bm{r}_{i}, \bm{r}_{i+1}, \bm{r}_{i+2}, \cdots\}$ から曲線

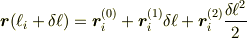
$\bm{r}(\ell_i+\delta\ell) = \bm{r}^{(0)}_i + \bm{r}^{(1)}_i\delta\ell + \bm{r}^{(2)}_i\frac{\delta\ell^2}{2}$

のベクトル係数(必要なのは 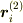$\bm{r}^{(2)}_i$ )を求める方法が良いと思います．(最小二乗法については文献に当たるか，Exelなどのアプリケーションの解説を参考にしてください．)

もちろんこの方法でも上で述べた条件「切片長 << 曲率半径」，あるいはフレームレート(1/30s)を意識した同値な条件「角速度 << 30 rad/s」，を満たさないと正しい結果は出ません．

# 通常のビデオカメラだと1/10秒間に約半回転をする角速度より遙かに小さい角速度の運動でないとだめ(理想は1秒間に半回転の運動)ですから，計測したい運動によっては高速ビデオカメラを使う必要があるかもしれませんね．

Re: 曲率半径，瞬間中心を求めたい

スパイクさんのレス (2007/09/21(Fri) 01:53)

横返信失礼致します．

toorisugari no Hiroさんの算出方法で，特に問題は感じられません．＃正攻法かと思われます．

Re: 曲率半径，瞬間中心を求めたい

オリーブを愛する者さんのレス (2007/09/21(Fri) 09:28)

分かりやすくご返信いただき，感謝しております．誤差や計測上のご注意まで教えていただき，大変勉強になりました．この方法でやって見ます．ありがとうございました．

疑問が生じました．

オリーブを愛する者さんのレス (2007/09/21(Fri) 16:07)

単位接ベクトルの変化率を求める式（２階微分の式）で，分母のδliを表す式の説明でi+1/2の切片長とi-1/2の切片長を2で割った値が出てきていますが，これはなぜなんでしょうか．

それから瞬間中心の位置を求める式がなぜそうなるのかが分かりません．教えてください．よろしくお願いします．

Re: 疑問が生じました．

toorisugari no Hiro さんのレス (2007/09/21(Fri) 17:21)

> 瞬間中心の位置を求める式がなぜそうなるのかが分かりません．

えっと，結構きつい質問ですね．

すこしまじめに証明しましょうか． http://www12.plala.or.jp/ksp/vectoranalysis/FrenetFrame/ http://www12.plala.or.jp/ksp/vectoranalysis/Curvature/ を参考にしてください．

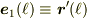
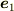単位ベクトルを $\bm{e}_1(\ell)\equiv \bm{r}'(\ell)$ $\bm{e}_2(\ell)\equiv R\bm{r}''(\ell) \qquad (R=1/|\bm{r}''(\ell)|)$ と定義します．( $\bm{e}_1$ が単位ベクトルであることは先の文献を読んでください．)

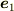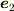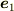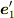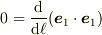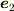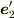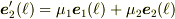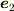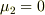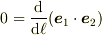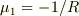$\bm{e}_1$ と $\bm{e}_2$ が直交することは， $\bm{e}_1$ と $\bm{e}_1'$ が直交する事，つまり， $0=\frac{\mathrm{d}}{\mathrm{d} \ell}(\bm{e}_1\cdot\bm{e}_1)$ から自明ですね．同様に $\bm{e}_2$ と $\bm{e}_2'$ が直交する事もわかります．いま，2次元をかんがえているので， $\bm{e}_2'(\ell)=\mu_1\bm{e}_1(\ell)+\mu_2\bm{e}_2(\ell)$ と展開できるはずですが， $\bm{e}_2$ を内積でかけると $\mu_2=0$ が，さらに $0=\frac{\mathrm{d}}{\mathrm{d} \ell}(\bm{e}_1\cdot\bm{e}_2)$ から $\mu_1=-1/R$ が導けます．

つまり，

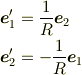
$\bm{e}_1' &= \frac{1}{R} \bm{e}_2\\\bm{e}_2' &= -\frac{1}{R} \bm{e}_1$

ですね．

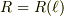ここで $R=R(\ell)$ は定数と仮定します．このとき

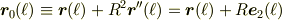
$\bm{r}_0(\ell) \equiv \bm{r}(\ell) + R^2 \bm{r}''(\ell) = \bm{r}(\ell) + R \bm{e}_2(\ell)$

を 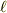$\ell$ で微分すると

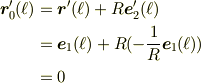
$\bm{r}_0'(\ell) &= \bm{r}'(\ell) + R \bm{e}_2'(\ell)\\&= \bm{e}_1(\ell) + R (-\frac{1}{R} \bm{e}_1(\ell))\\&= 0$

となり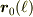， $\bm{r}_0(\ell)$ は動きません．

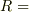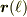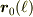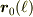つまり，一定のとき， $\bm{r}(\ell)$ は定点 $\bm{r}_0(\ell)$ から一定距離で運動，すなわち，円運動をします．これより $\bm{r}_0(\ell)$ は円の中心，が円の半径であることがわかります．

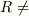$R\ne$ 一定の場合も局所的にみれば円運動と考えられますから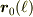， $\bm{r}_0(\ell)$ を瞬間中心，を曲率半径とよびます．

> 単位接ベクトルの変化率を求める式（２階微分の式）で，分母の |ca0ebab728184dc58d601e06d193f9ac| を表す式の説明で |82f72b525a6b17d285f666084e8784c8| の切片長と |9828dbc6d0215b40e8308c5b252055c4| の切片長を2で割った値が出てきていますが，これはなぜなんでしょうか．

「平均で近似したから」ではダメですか?

じゃあ別の手．1次のテーラー展開

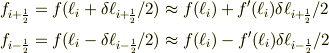
$f_{i+\frac{1}{2}} &= f(\ell_i + \delta \ell_{i+\frac{1}{2}}/2) \approx f(\ell_i) + f'(\ell_i) \delta \ell_{i+\frac{1}{2}}/2\\f_{i-\frac{1}{2}} &= f(\ell_i - \delta \ell_{i-\frac{1}{2}}/2) \approx f(\ell_i) - f'(\ell_i) \delta \ell_{i-\frac{1}{2}}/2$

より

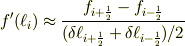
$f'(\ell_i) \approx \frac{f_{i+\frac{1}{2}}-f_{i-\frac{1}{2}}}{(\delta \ell_{i+\frac{1}{2}}+\delta \ell_{i-\frac{1}{2}})/2}$

となりますよね．(これは中心差分の不等間隔版です．)

Re: 疑問が生じました．

スパイクさんのレス (2007/09/23(Sun) 18:20)

大丈夫かと思われます．＃テーラー展開しておくと，後々の適用もしやすいでしょうし．

Re: 疑問が生じました．

オリーブを愛する者さんのレス (2007/09/28(Fri) 11:54)

ありがとうございました．勉強になります．助かりました．

[home] [掲示板] [ページの先頭]