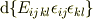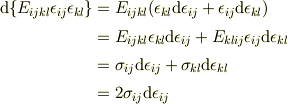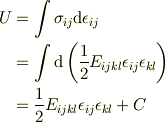歪エネルギ密度の導出

歪エネルギ密度の導出

よしぼー さんの書込 (2007/09/18(Tue) 17:02)

はじめまして．

(等方)線形弾性体の歪エネルギ密度の導出について，

先ず，歪エネルギ密度の定義は

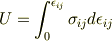
U=\int_{0}^{\epsilon_{ij} } \sigma_{ij} d\epsilon_{ij}

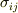? ( \sigma_{ij} ：応力テンソル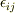， \epsilon_{ij} ：歪テンソル) であり， この定義に線形弾性体の構成式

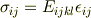
\sigma_{ij} =E_{ijkl} \epsilon_{ij}

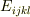? ( E_{ijkl} :弾性係数テンソル)

を用いて

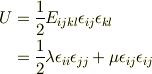
U &= \frac{1}{2} E_{ijkl} \epsilon_{ij} \epsilon_{kl} \\&= \frac{1}{2} \lambda \epsilon_{ii} \epsilon_{jj} + \mu \epsilon_{ij} \epsilon_{ij}

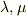? ( \lambda,\mu :lameの定数) となる，という結果は知っているのですが，この式展開についての疑問です．

疑問点は，

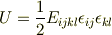
U &= \frac{1}{2} E_{ijkl} \epsilon_{ij} \epsilon_{kl}

はなぜこのようになるのかがよく分からず，その導出を御教授いただきたいということと，それから

2.等方線形弾性体ということで，

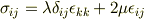
\sigma_{ij} =\lambda \delta_{ij} \epsilon_{kk} +2\mu \epsilon_{ij}

を?に代入して

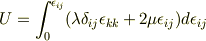
U=\int_{0}^{\epsilon_{ij} }(\lambda \delta_{ij} \epsilon_{kk} +2\mu \epsilon_{ij} ) d\epsilon_{ij}

となるので，?の二行目の式の第2項はすぐに理解できるのですが， 第1項がなぜこのようになるのかがよく理解できないでいて，式展開の詳細を御教授いただきたいということです．

どうかよろしくお願いいたします．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 17:21)

第2式 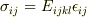\sigma_{ij} =E_{ijkl} \epsilon_{ij} は間違いで，正しくは 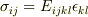\sigma_{ij} =E_{ijkl} \epsilon_{kl} ですよね．

また，(等方)弾性係数テンソル 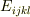E_{ijkl} にはどのような性質がありますか？

Re: 歪エネルギ密度の導出

よしぼー さんのレス (2007/09/18(Tue) 17:27)

> toorisugari no Hiro さん ご指摘のとおりです．失礼しました．

等方弾性係数テンソルですから，添字についての入替

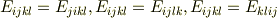
E_{ijkl}=E_{jikl},E_{ijkl}=E_{ijlk},E_{ijkl}=E_{klij}

としてよい(ということをご指摘されているのでしょうか)．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 17:49)

> 等方弾性係数テンソルですから，添字についての入替 > 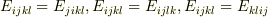E_{ijkl}=E_{jikl},E_{ijkl}=E_{ijlk},E_{ijkl}=E_{klij} > としてよい(ということをご指摘されているのでしょうか)．

最後の 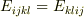E_{ijkl}=E_{klij} と部分積分(およびdummy indexの入れ替え)を使えば

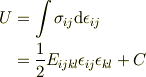
U &=\int \sigma_{ij} \mathrm{d}\epsilon_{ij} \\&= \frac{1}{2} E_{ijkl} \epsilon_{ij} \epsilon_{kl} +C

は導出できると思います．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 17:54)

テンソルに対する部分積分がわからなければ

\mathrm{d}\{ E_{ijkl} \epsilon_{ij} \epsilon_{kl} \}

を計算するのも手です．

Re: 歪エネルギ密度の導出

よしぼー さんのレス (2007/09/18(Tue) 18:04)

> toorisugari no Hiro さん

>最後の 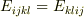E_{ijkl}=E_{klij} と部分積分(およびdummy indexの入れ替え)を使えば

というところを是非お示しいただけないでしょうか？ 大変お手数をおかけして本当に恐縮なのですが，分かっておられる方には当たり前でも，言われておおっと思って理解するまで自分だけは分からない，というような場面もあるかと思いますゆえ…

すいませんが，お願いできないでしょうか．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 18:09)

> すいませんが，お願いできないでしょうか．

No.17888を途中まででいいですから考えてみてください．

Re: 歪エネルギ密度の導出

よしぼー さんのレス (2007/09/18(Tue) 18:21)

No.17888に気づいておりませんでした．すいません．

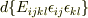d\{ E_{ijkl} \epsilon_{ij} \epsilon_{kl} \} ですよね…

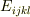E_{ijkl} は(少なくとも今は)定数と考えてよいはずで，したがって

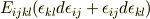
E_{ijkl} (\epsilon_{kl} d\epsilon_{ij} +\epsilon_{ij} d\epsilon_{kl} )

あ，なんとなく見えた気がします．ここから 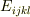E_{ijkl} を2通りに使って， 上式は

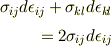
\sigma_{ij} d\epsilon_{ij} +\sigma_{kl} d\epsilon_{kl} \\=2\sigma_{ij} d\epsilon_{ij}

となるのですね．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 18:25)

> となるのですね．

おめでとうございます．そのとおりです．

あともおなじ考え方でできるはずですから，他の人のために解法を書いてもらえますか?

> (少なくとも今は)定数と考えてよいはずで

線形弾性体ですから定数ですね．

Re: 歪エネルギ密度の導出

よしぼー さんのレス (2007/09/18(Tue) 18:56)

今の過程を逆に辿ればいいはずだと思うのですが…

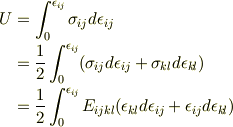
U &= \int_{0}^{\epsilon_{ij}} \sigma_{ij} d\epsilon_{ij} \\&= \frac{1}{2} \int_{0}^{\epsilon_{ij}} (\sigma_{ij} d\epsilon_{ij} +\sigma_{kl} d\epsilon_{kl}) \\&= \frac{1}{2} \int_{0}^{\epsilon_{ij}} E_{ijkl} (\epsilon_{kl} d\epsilon_{ij} +\epsilon_{ij} d\epsilon_{kl} )

ここで詰まってしまいます．先ほど言われていた部分積分の話題なのかと思うのですが．

すいません．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 19:09)

定積分表示は誤解を招きやすいので不定積分で計算した方がいいです．

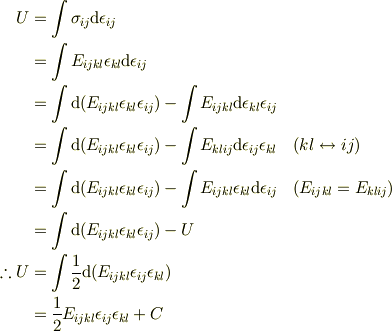
U &= \int \sigma_{ij} \mathrm{d}\epsilon_{ij} \\ &= \int E_{ijkl} \epsilon_{kl} \mathrm{d}\epsilon_{ij}\\&= \int \mathrm{d}(E_{ijkl} \epsilon_{kl} \epsilon_{ij}) - \int E_{ijkl} \mathrm{d}\epsilon_{kl} \epsilon_{ij}\\&= \int \mathrm{d}(E_{ijkl} \epsilon_{kl} \epsilon_{ij}) - \int E_{klij} \mathrm{d}\epsilon_{ij} \epsilon_{kl} \quad (kl \leftrightarrow ij)\\&= \int \mathrm{d}(E_{ijkl} \epsilon_{kl} \epsilon_{ij}) - \int E_{ijkl} \epsilon_{kl} \mathrm{d}\epsilon_{ij} \quad (E_{ijkl}=E_{klij})\\&= \int \mathrm{d}(E_{ijkl} \epsilon_{kl} \epsilon_{ij}) - U\\\therefore U&= \int \frac{1}{2} \mathrm{d}(E_{ijkl} \epsilon_{ij}\epsilon_{kl}) \\&= \frac{1}{2} E_{ijkl} \epsilon_{ij}\epsilon_{kl} + C

が最初の式の導出ですね．

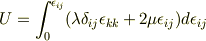
U=\int_{0}^{\epsilon_{ij} }(\lambda \delta_{ij} \epsilon_{kk} +2\mu \epsilon_{ij} ) d\epsilon_{ij}

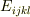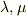も同様の考え方ができるはずです． それか E_{ijkl} を直接 \lambda,\mu で表してみるのも良いかと思います．

Re: 歪エネルギ密度の導出

よしぼー さんのレス (2007/09/18(Tue) 19:29)

お示しいただいた，最初の式の不定積分のほうはもう大丈夫です． 定積分でうまく理解できないのは気持ち悪い気もしないではないですが…

2番目の式

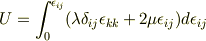
U=\int_{0}^{\epsilon_{ij} }(\lambda \delta_{ij} \epsilon_{kk} +2\mu \epsilon_{ij} ) d\epsilon_{ij}

の第1項については，

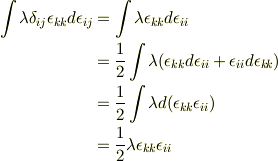
\int \lambda \delta_{ij} \epsilon_{kk} d\epsilon_{ij} &= \int \lambda \epsilon_{kk} d\epsilon_{ii} \\&= \frac{1}{2} \int \lambda (\epsilon_{kk} d\epsilon_{ii}+\epsilon_{ii} d\epsilon_{kk}) \\ &= \frac{1}{2} \int \lambda d(\epsilon_{kk} \epsilon_{ii}) \\&= \frac{1}{2} \lambda \epsilon_{kk} \epsilon_{ii}

という具合でよいのでしょうか．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 19:30)

先の記事ではバカ正直にやりましたが，

\mathrm{d}\{ E_{ijkl} \epsilon_{ij} \epsilon_{kl} \}&= E_{ijkl} (\epsilon_{kl} \mathrm{d}\epsilon_{ij} +\epsilon_{ij} \mathrm{d}\epsilon_{kl} )\\&= E_{ijkl} \epsilon_{kl} \mathrm{d}\epsilon_{ij} +E_{klij}\epsilon_{ij} \mathrm{d}\epsilon_{kl}\\&= \sigma_{ij} \mathrm{d}\epsilon_{ij} +\sigma_{kl} \mathrm{d}\epsilon_{kl}\\&= 2\sigma_{ij} \mathrm{d}\epsilon_{ij}

従って

U&= \int \sigma_{ij} \mathrm{d}\epsilon_{ij}\\&= \int \mathrm{d}\left(\frac{1}{2} E_{ijkl} \epsilon_{ij}\epsilon_{kl} \right) \\ &= \frac{1}{2} E_{ijkl} \epsilon_{ij}\epsilon_{kl} + C

の方がわかりやすいですね．

Re: 歪エネルギ密度の導出

toorisugari no Hiro さんのレス (2007/09/18(Tue) 19:37)

> という具合でよいのでしょうか．

はい．そうです．

> 定積分でうまく理解できないのは気持ち悪い気もしないではないですが…

今計算してるのは1次元での定積分ではなく9次元空間(独立な成分は6個)における線積分なのです(始点終点のみで経路は明示されていません)． 先に示された表示は

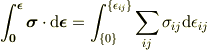
\int_{\bm{0}}^{\bm{\epsilon}} \bm{\sigma}\cdot\mathrm{d}\bm{\epsilon} &=\int_{\{0\}}^{\{\epsilon_{ij}\}} \sum_{ij} \sigma_{ij}\mathrm{d}\epsilon_{ij}

と表示すべきものです．

9次元空間の経路を具体的に考えて定積分するより，全微分が存在するのですから経路を考えず不定積分で計算し，最後に始点終点を考えた方が簡単です．

Re: 歪エネルギ密度の導出

よしぼー さんのレス (2007/09/18(Tue) 19:52)

最初に提示した式は，もともと私が参考にしたテキストからそのまま引っ張ってきたものですから，私が特に表記方法についてこだわりを持って意図して書いたものではないことはご容赦ください．その点にどうしても深入りしたいというわけではありません．

しばらく考えていて分からなかったことが無事解決できました． toorisugari no Hiro さん，お話できて嬉しく思います．また疑問なことがあった際はお力を貸していただければと思います．

本当にありがとうございました．