出生の秘密を
出生の秘密を
G さんの書込 (2007/09/06(Thu) 19:49)
【早稲田大の(n∈Rで構わない)係数に あのような複雑(でもないが)怪奇なパラメタ-が定められている
ことのPn(x)∈R[x]の出生の秘密を暴きたくなる筈】
Re: 出生の秘密を
クロメル さんのレス (2007/09/07(Fri) 12:10)
クロメル@旅先です. 携帯からなので,数式は書きづらいです.
添付画像にあった早稲田の過去問について途中報告します. 不思議な問題ですね. 解の一つをtと置くと,Pn(t)=0が成立し,これを使い,Pn(x)=0から,パラメータnを消去します.
その式は,x=tを解に持つので,この三次式は二次方程式の解の公式で因数分解できます.
このでてくる解g(t)とg*g(t)というのが,変わっていて, g*g(t)=g^(-1)(t) (この関数の合成は逆関数)となるようですね.
Re: 出生の秘密を
Re: 出生の秘密を
クロメル さんのレス (2007/09/23(Sun) 23:52)
この問題は,Gさんの中ではもう解決しましたか?
あの後考えてみたのですが,僕の結論としては, これは問題を作る際に,パラメータ入りの三次方程式の解から,パラメータを消去して でてくる三次方程式の解を,g・g(t)=g^(-1)(t)を満たすgを用いて, (x-t)(x-g(t))(x-g^(-1)(t))になるように作っただけと言う結論になったことを報告します.
作る際にうまく作っただけであって,深い理論はないような気が….
…って,Gさんの新しい問題見ましたが,グレブナー基底とかが関係しているのですか. 奥が深そうですね(^^;)
gはn次多項式とすると,g・gはn^2次になりますから, g・g(t)=g^(-1)(t)を満たすなら次数は,0次. つまり,gは同じ次数の多項式の商になっているということなのですね. だから,g(t)=(at+b)/(ct+d)がでてくるのか….
それとなるほど,行列が使えるんですね. g(t)=(at+b)/(ct+d)を
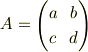
と表現できて, g・gは,A^2とうまく対応するんですね. いや,知りませんでした. おもしろいですね^^