過去スレ・反共ベクトルについて
過去スレ・反共ベクトルについて
シグモ さんの書込 (2007/09/05(Wed) 00:56)
反変・共変ベクトルの概念がよくわからなく,検索していたらここの掲示板の過去スレに引っかかったのですが,そのスレを見てもよくわからなかったので,質問させてください. かなり根本的なところがわかりません・・・
参照URL
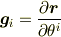
についてですが,
 が
が 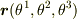 で表せるということですが,たとえば,
で表せるということですが,たとえば, 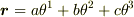 のように表せるということでしょうか?
ここまでOKでしょうか?
その場合,
のように表せるということでしょうか?
ここまでOKでしょうか?
その場合, 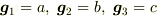 ということなのでしょうか?
ということなのでしょうか?
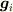 が単なる数字のような気がするのですが,これはベクトルなのですか?
が単なる数字のような気がするのですが,これはベクトルなのですか?
Re: 過去スレ・反共ベクトルについて
toorisugari no Hiro さんのレス (2007/09/05(Wed) 12:02)
>
> についてですが,
>  が
が 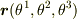 で表せるということですが,たとえば,
で表せるということですが,たとえば, 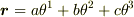 のように表せるということでしょうか?
のように表せるということでしょうか?
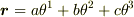 は左辺はベクトル,右辺はスカラーですので式として無意味です.(
は左辺はベクトル,右辺はスカラーですので式として無意味です.( 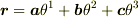 なら意味があります.これは直線斜交座標系になります.)
なら意味があります.これは直線斜交座標系になります.)
今,3次元ユークリッド空間を考えていますので,自然な直角座標系(直線直交座標系)がとれます.そのときの正規直交基底を 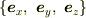 とします.
とします.  が
が 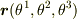 で表せるとは,
で表せるとは,
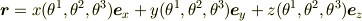
ということです.極座標系では
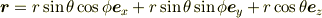
と表せますよね.この右辺を 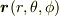 と表せば上の例に該当しますね.
と表せば上の例に該当しますね.
Re: 過去スレ・反共ベクトルについて
シグモ さんのレス (2007/09/07(Fri) 07:47)
ありがとうございます.理解できました.
もう一つ続けて質問させて下さい.
他のサイトで見た知識なのですが, 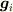 のように下に添え字が付いてるのは「共変ベクトル」と書いてありました.
極座標も共変ベクトルでに含まれるのでしょうか?
のように下に添え字が付いてるのは「共変ベクトル」と書いてありました.
極座標も共変ベクトルでに含まれるのでしょうか?
Re: 過去スレ・反共ベクトルについて
toorisugari no Hiro さんのレス (2007/09/07(Fri) 18:53)
> 他のサイトで見た知識なのですが, 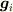 のように下に添え字が付いてるのは「共変ベクトル」と書いてありました.
のように下に添え字が付いてるのは「共変ベクトル」と書いてありました.
間違って理解されています.普通「共変ベクトル」と呼ばれるものは
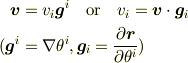
で表現される成分 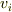 のことで,私は「ベクトル
のことで,私は「ベクトル  の共変成分」と呼ぶのが好きです.
の共変成分」と呼ぶのが好きです.
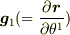 に特に名前はありません.強いて言うなら「曲線
に特に名前はありません.強いて言うなら「曲線 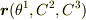 (2曲面
(2曲面 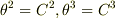 の交線)の接ベクトル」でしょうか.
の交線)の接ベクトル」でしょうか.
> 極座標も共変ベクトルでに含まれるのでしょうか?
申し訳ないですが,意味不明です.「座標(系)」とベクトルあるいは成分は別の概念です.
Re: 過去スレ・反共ベクトルについて
zoro さんのレス (2007/09/07(Fri) 20:33)
横から失礼します.
厳密では在りませんが,イメージを浮かべる為に2次元の直交座標系と斜交座標系を考えて見ます.
図は,以前 eKineticさんのスレッドで書いたのをベースに書きます.
・複素平面の原点Oの実軸にx,虚軸にyとする直交座標系,Oxy. ・そのx時から,θu,θvの角度の方向に,斜交軸,e^(iθu)とe^(iθv)を考えて,原点からの長さを u,vとする.
<pre>
i
|grad v: 「v一定のライン」の法線⊥e^(iθu)
|  /
| /
y ・−−−−−−−−−−−−−−−−−−−−−−−・P
| //
|v一定のライン →/ /|
| // |
| / /|
|e^(iθv) // ←u一定のライン‖e^(iθv)
| / / /|
|/ // 「u一定のライン」の法線:grad u⊥e^(iθv)
| // /
/
| /
y ・−−−−−−−−−−−−−−−−−−−−−−−・P
| //
|v一定のライン →/ /|
| // |
| / /|
|e^(iθv) // ←u一定のライン‖e^(iθv)
| / / /|
|/ // 「u一定のライン」の法線:grad u⊥e^(iθv)
| // /  |/ // |
| / / / |
|/ // |
| // /|
| v / / |
|/ // |
| / / / |
|/ // |
| // /|
| v / / |
・・ /e^(iθu) |
|/ / /| | / / /| |/ / /| | / /| |/ ・u | | / /| | / /| | / /| |/ /| | / /| |/ /|
| / /|
|/ /| | / /| | / /| | / /| |/ /| | // | |/| ・−−−−−−−−−−−−−−−−−−−−−−−・−−−−− 1 O x
</pre>
こうすると 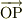 はそれぞれの座標系から,
はそれぞれの座標系から,
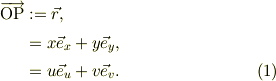
それぞれの座標系の座標値間の関係を誘導し易くする為に,複素数表示に移行すると,
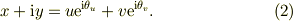
陽に,座標間の関係を書けば判るように,角度をパラメータにした一時変換です.従って,uやv一定のラインに垂直な法線ヴェクタを気楽に求められます.
先ず,式(1)より,直交系では,
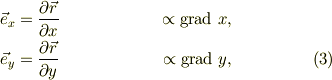
である.
同様に,
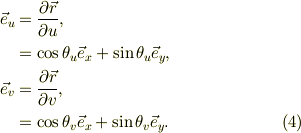

ここで,

そこで,式(5)を実行する為に,式(2)を具体的に書き下せば,
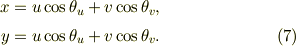
逆に解けば,
![u &= \frac{1}{J}[ x\sin \theta_v -y\cos \theta_v ],\\v &= \frac{1}{J}[ x\sin \theta_u -y\cos \theta_u ]. \tag{8}](http://hooktail.maxwell.jp/bbslog/aa350d3be512ec50624417c3986b0b66.png)
ここで
![J := [ \cos \theta_u \cdot \sin \cos \theta_v-\cos \theta_v \cdot \sin \cos \theta_u]. \tag{9}](http://hooktail.maxwell.jp/bbslog/905b8c6f494917fd5a9dde35f1712399.png)
式(8)を式(5)に適用すれば,
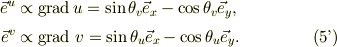
この式(5')は式(6)の直交性を満たす.
以上の,幾何学的な関係はイメージとして把握されえると思いますが,次のMXKさんのおっしゃる「反変成分,反変基底,共変成分,共変基底」として,どのような物理的な理解をして行けば良いのか,私も興味深く拝見したいと思います.
折角,物理数学に明るい方々がいらっしゃるので,添字の上下で幾何学的な性格が分類されるというような所から,一歩踏み入れた解説をお願い出来ると幸いです.
ただ,外していたら,ご免なさい.
Re: 過去スレ・反共ベクトルについて
MXK さんのレス (2007/09/07(Fri) 22:29)
何と呼ぶかはともかくとして,
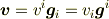
のように4人のプレイヤーがいるので,それぞれ名前をつけたいところですね. 反変成分,反変基底,共変成分,共変基底とでも呼ぶのでしょうか.
Re: 過去スレ・反共ベクトルについて
toorisugari no Hiro さんのレス (2007/09/08(Sat) 00:16)
> 反変成分,反変基底,共変成分,共変基底とでも呼ぶのでしょうか.
この命名が自然かなと思います.
もっとも「反変基底」って何かわかったようなわからないような....そもそも「反変・共変」って名前がもはや古いのではないかと思います. # 代案は....ないですが....
Re: 過去スレ・反共ベクトルについて
zoro さんのレス (2007/09/08(Sat) 21:41)
斜交座標の場合の,座標値の取り方に2種類ある事に今頃気づきました.もはやアスキー・アートでは表現が難しそうなので,拝見したサイトの一つを示します.
・Log - 共変,反変( 2 ) h ttp://www.h6.dion.ne.jp/~xylapone/log2/math/vector4.html
Re: 過去スレ・反共ベクトルについて
zoro さんのレス (2007/09/09(Sun) 00:55)
素人なりに,2次元平面での座標表現の考え方を整理してみた;
- 座標のフレームとして原点と,2つの独立した方向が定まり,
- 考察点と原点とで平行四辺形を作り,計量するか,
- 考察点からフレームに垂線を引いて新たなフレームを作り,計量する.
以下に,図示してみよう.
#結果として,上のページでご紹介したサイトと同じになったのですが, #こちらの論議の為には,ここでの表示の方が引用しやすいと考えました.
<pre> =============================== ■■■■■■■■■■■■■■■■■■■ ■手順1:座標のフレームを決める■ ■■■■■■■■■■■■■■■■■■■
●原点Oと異なる2点U,Vを決める.フレーム,O-UVの出現!
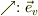 V
/
/
/
/
/
/
/
/
/
/
/
/∠A
・────────────────────U
V
/
/
/
/
/
/
/
/
/
/
/
/∠A
・────────────────────U 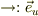 O
</pre>
O
</pre>
#素人意見 # #この段階で,OU,OVの方向を示す単位ヴェクタが付与されると考えたい. #これら単位ヴェクタは,「解析的に与えられる」のではなく,先験的に存在すると思う.
<pre> =============================== ■■■■■■■■■■■■■■■■■■■■■■■■■■ ■手順2:任意点からフレームに平行線を出す方式■ ■■■■■■■■■■■■■■■■■■■■■■■■■■
●平面中の任意点Pの位置を特定する為に,
・その点から,フレームの線,OU, OVに平行線を引き,
・その線とフレームとの交点と原点Oとの長さを,座標値,u,vとする.
・ 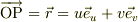
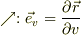 V
/
/
/
/
/ ∠A
v ・──────────・P
//
//
//
//
//
/∠A / ∠A
・──────────・─────────U
O u
V
/
/
/
/
/ ∠A
v ・──────────・P
//
//
//
//
//
/∠A / ∠A
・──────────・─────────U
O u
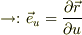 </pre>
<pre>
===============================
■■■■■■■■■■■■■■■■■■■■■■■■■■
■手順3:任意点からフレームに垂線線を出す方式■
■■■■■■■■■■■■■■■■■■■■■■■■■■
</pre>
<pre>
===============================
■■■■■■■■■■■■■■■■■■■■■■■■■■
■手順3:任意点からフレームに垂線線を出す方式■
■■■■■■■■■■■■■■■■■■■■■■■■■■
●平面中の任意点Pの位置を特定する為に,
・その点から,フレームの線,OU, OVに垂線を引き,
・原点Oから2つの垂線に並行に新たなフレーム,O-V⊥U⊥を作り,
・最初に書いた2つの垂線と原点Oとフレームとの交点の座標値,v⊥,u⊥とする.
・ 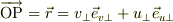
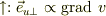
U⊥ │ │
u⊥・
│ │ │ │ │ │ │
│ V
│ /
│ /
│ /
│ ・ ?
│/ 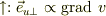 │/
│/ 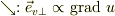 │/ │/ /
│/ /
│v ・──────────・P── v一定ライン
│//│
│//│
│//│
│//│
│//│
│/∠A /│?
│/ │/ /
│/ /
│v ・──────────・P── v一定ライン
│//│
│//│
│//│
│//│
│//│
│/∠A /│?
- O・──────────・──────・──U
- │/ u│ │/│ │u一定ライン │ ││ ││ ││ ││ ││ ││ ││ ││ ││ ││ ││ ││ ││ ││ │ v⊥ ・ ││││││
V⊥
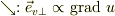
・直交性
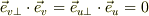
=============================== </pre>
●●●●●●●●●● ●作図後の感想●2007-09-10 00:05 ●●●●●●●●●●
●いつも,書いてみたいと思っていたが,想像以上に面白かった.●
(1)斜交座標は,もろに菱形座標である事を,再認識した. (2)最初の座標,O-UVは,解析処理とは別に独立して構築出来る. (3)でも,O-UVを作ってしまえば,その基底ヴェクタは; 位置のヴェクタについての座標値;u or v,の偏微分による接線ヴェクタとして再定義が出来る. (4)O-UV系の,座標値が一定のライン(3次元なら面)の法線を勾配演算子(grad)で定めることが出来て,O-U⊥V⊥を得る事ができた. 2次元で,図示したので,簡単に新基底ヴェクタを決められたが,本来は,元基底の外積が絡むだろうと推定する. (5)O-U⊥V⊥で,再度(4)の処理をすれば,明らかにO-UVに戻るのが容易に観察される. これは,線形な座標変換であるから言える事か? (6)作図に現れた基底ヴェクタとその座標値を,共変・反変という観点から; 「どのように解釈できるのか?」を知りたいと感じます.
Re: 過去スレ・反共ベクトルについて
toorisugari no Hiro さんのレス (2007/09/14(Fri) 01:19)
> 何と呼ぶかはともかくとして,
> 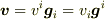 > のように4人のプレイヤーがいるので,それぞれ名前をつけたいところですね.
> 反変成分,反変基底,共変成分,共変基底とでも呼ぶのでしょうか.
> のように4人のプレイヤーがいるので,それぞれ名前をつけたいところですね.
> 反変成分,反変基底,共変成分,共変基底とでも呼ぶのでしょうか.
念のため.
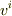 : 反変成分
: 反変成分
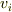 : 共変成分
: 共変成分
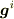 : 反変基底
: 反変基底
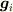 : 共変基底
ですよね.
: 共変基底
ですよね.
Re: 過去スレ・反共ベクトルについて
MXK さんのレス (2007/09/14(Fri) 23:02)
> 念のため.
> 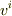 : 反変成分
>
: 反変成分
> 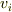 : 共変成分
>
: 共変成分
> 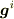 : 反変基底
>
: 反変基底
> 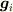 : 共変基底
> ですよね.
: 共変基底
> ですよね.
その通りです. ご指摘ありがとうございます.
反変 x 共変=不変
ということですね.
Re: 過去スレ・反共ベクトルについて
toorisugari no Hiro さんのレス (2007/09/15(Sat) 01:04)
MXKさん 実は前から気になってなっていたのでお聞きしたいのですが,
よく見る定義にある, 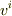 を「反変ベクトル(成分)」,
を「反変ベクトル(成分)」, 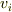 を「共変ベクトル(成分)」とよぶのは,(計量のはいった)ベクトル空間
を「共変ベクトル(成分)」とよぶのは,(計量のはいった)ベクトル空間 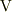 に属するベクトル
に属するベクトル 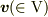 の2種類の自然基底
の2種類の自然基底 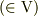 で採った成分,すなわち,「ベクトルの反変成分」「ベクトルの共変成分」の事だととらえていました.
# つまり「反変・共変」は基底の区別
で採った成分,すなわち,「ベクトルの反変成分」「ベクトルの共変成分」の事だととらえていました.
# つまり「反変・共変」は基底の区別
でも,主流な考え方は,それぞれ違うベクトル空間に属するベクトル(の成分)という意味で使っているのかなと気づきました.
つまり,「
ベクトル空間 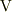 に属するベクトル
に属するベクトル 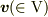 を
を 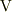 の基底で採った成分
の基底で採った成分 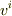 を「反変ベクトル(成分)」とよび,
双対なベクトル空間
を「反変ベクトル(成分)」とよび,
双対なベクトル空間 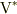 に属するベクトル
に属するベクトル 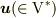 を
を 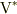 の(双対)基底で採った成分
の(双対)基底で採った成分 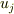 を「共変ベクトル(成分)」とよぶ.
# つまり「反変・共変」は空間の区別
」
という解釈なのかと思うのですが,正しいでしょうか?
を「共変ベクトル(成分)」とよぶ.
# つまり「反変・共変」は空間の区別
」
という解釈なのかと思うのですが,正しいでしょうか?
# 後者に計量が入っているなら,どちらの考えでもおなじだとは思うのですが....
Re: 過去スレ・反共ベクトルについて
MXK さんのレス (2007/09/16(Sun) 13:08)
toorisugari no Hiro さん,
おっしゃるように,本来的には双対構造にかかわるものであって,
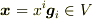
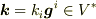 のように別空間なのでしょうね.
のように別空間なのでしょうね.
内積があると, 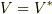 なので区別はなくなる
のでしょうが,完全に区別がなくなるのは正規直交基底と
その成分を使う場合です.
何らかの事情で,非正規基底や非直交基底を使う場合には,
区別が必要になります.
なので区別はなくなる
のでしょうが,完全に区別がなくなるのは正規直交基底と
その成分を使う場合です.
何らかの事情で,非正規基底や非直交基底を使う場合には,
区別が必要になります.
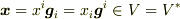
内積空間でも,双対構造をつかった方が自然な場面があると いうことでしょうか.
Re: 過去スレ・反共ベクトルについて
シグモ さんのレス (2007/09/17(Mon) 19:24)
スレを立てたシグモです
色々な変数が出てきて頭が混乱しています. 話を戻すようで大変申し訳ないのですが,
斜交座標の基底 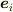 から特殊な変換をして得られるのが,別の斜交座標の基底である反変,共変ベクトルだと思っていたのですが,これは勘違いでしょうか?
から特殊な変換をして得られるのが,別の斜交座標の基底である反変,共変ベクトルだと思っていたのですが,これは勘違いでしょうか?
Re: 過去スレ・反共ベクトルについて
スパイク さんのレス (2007/09/17(Mon) 20:43)
シグモさん,こんばんは.
>斜交座標の基底から特殊な変換をして得られるのが,別の斜交座標の基底である >反変,共変ベクトルだと思っていたのですが,これは勘違いでしょうか?
座標変換の話ですから,間違いありません.
Re: 過去スレ・反共ベクトルについて
シグモ さんのレス (2007/09/17(Mon) 21:23)
よく出てくる 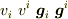 のうち,とれが反変ベクトルでどれが共変ベクトルなのですか?
のうち,とれが反変ベクトルでどれが共変ベクトルなのですか?
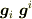 が基底[ベクトル]なのかと思っていました.
が基底[ベクトル]なのかと思っていました.
Re: 過去スレ・反共ベクトルについて
スパイク さんのレス (2007/09/17(Mon) 21:55)
匿名投稿は,一見個人が特定されないように思い込む方は多いとは思うのですが,
>とれが反変ベクトルでどれが共変ベクトルなのですか?
出来れば,座標変換の成書をきちんと読まれることをお勧めしたいかと思います.
Re: 過去スレ・反共ベクトルについて
MXK さんのレス (2007/09/17(Mon) 23:21)
シグモさん
あまり用語にとらわれず, 実際に斜交座標を描いて,自分でいろいろ考えてみるのもいいかも知れません.
- 裏の座標(双対座標)の必要性
- 1つのベクトルをそれぞれの座標であらわす
(3) もう一つ別の表の座標を導入する ...
Re: 過去スレ・反共ベクトルについて
toorisugari no Hiro さんのレス (2007/09/18(Tue) 15:04)
> 斜交座標の基底 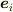 から特殊な変換をして得られるのが,
> 別の斜交座標の基底である反変,共変ベクトルだと思っていたのですが,
> これは勘違いでしょうか?
から特殊な変換をして得られるのが,
> 別の斜交座標の基底である反変,共変ベクトルだと思っていたのですが,
> これは勘違いでしょうか?
ごめんなさい.意味がつかめません.
> よく出てくる |279f21e0aae622331b6498e07cfdbc76| のうち, > とれが反変ベクトルでどれが共変ベクトルなのですか? > |32e404bc6bbb55ca8a966a1a75f07848| が基底[ベクトル]なのかと思っていました.
その前に.
ベクトルというとき,その言葉は歴史的理由で2つの異なる概念を指すことを理解してもらわないといけません.たぶん,それを踏まえておられないので混乱されていると思います.
3次元線形空間 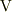 の元
の元  および一次独立な3つの元
および一次独立な3つの元 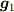 ,
, 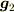 ,
, 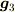 があるとします.3つの組を基底と呼び,その選び方は自由です(通常,座標系の選び方によります).このとき,ある数
があるとします.3つの組を基底と呼び,その選び方は自由です(通常,座標系の選び方によります).このとき,ある数 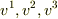 が存在して
が存在して
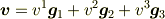
と書けます.この数の組 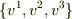 を
を  の成分と呼びます.
(存在が言えるだけで
の成分と呼びます.
(存在が言えるだけで  から
から 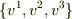 をどのように計算するかは不明です.もちろん逆は自明ですね.成分を計算するためには,双対線形空間を導入するか計量(=内積)を導入するかしないといけませんが,今は考えなくて良いです.)
をどのように計算するかは不明です.もちろん逆は自明ですね.成分を計算するためには,双対線形空間を導入するか計量(=内積)を導入するかしないといけませんが,今は考えなくて良いです.)
さて,基底を固定すると数表示
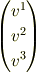
は元  と「同値関係」にあります.
と「同値関係」にあります.
そのため,ややこしい事に「元をベクトルとみる立場」と「数表示をベクトルとみる立場」のふたつの異なる考え方があるのです.そして「反変,共変ベクトル」という表現も,後者の考え方に基づいているのです.
座標変換をしても線形空間の元  は不変です.しかし,基底の取り方(線形空間から一次独立な3つの元
は不変です.しかし,基底の取り方(線形空間から一次独立な3つの元 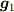 ,
, 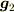 ,
, 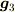 を選ぶ方法)は変わり,成分も追従して変わります.ということは自動的に数表示の値も変化します.
を選ぶ方法)は変わり,成分も追従して変わります.ということは自動的に数表示の値も変化します.
座標変換をしたとき, 「元をベクトル」という立場ではベクトルは不変です.成分が変わるだけです. 「数表示をベクトル」という立場では(元や基底の事は忘れています),数表示,すなわちベクトルは変化します.
繰り返しますと「反変ベクトル」という表現は「数表示をベクトル」という立場での概念であり,それが指すのは数表示すなわち成分の組 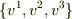 です(*).
です(*).
「元をベクトル」という立場では「反変,共変ベクトル」という概念は元々なく,元  をベクトル,
をベクトル, 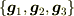 を(共変)基底,成分の組
を(共変)基底,成分の組 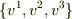 を(反変)成分と呼びます.
(基底の各要素の事を基底ベクトルと呼んでもいいですが,私には出来の悪い同義反復に聞こえます.)
を(反変)成分と呼びます.
(基底の各要素の事を基底ベクトルと呼んでもいいですが,私には出来の悪い同義反復に聞こえます.)
「数表示をベクトル」という立場は高校から連なる考え方で今でも認められていますが,個人的には古い考え方だと思います.
(*)反変,共変という言葉が接空間とその双対である余接空間をダブルミーニングで指してるようだというのが前の私の記事ですが,それは無視して結構です.
(追記 9/20:「縦表示」を「数表示」に変更しました.) (追記 11/7:「ベクトル空間」を「線形空間」に変更しました.)
Re: 過去スレ・反共ベクトルについて
スパイク さんのレス (2007/09/19(Wed) 21:47)
こんばんは.
>>とれが反変ベクトルでどれが共変ベクトルなのですか?
普通は,利用頻度の高い方を”反変ベクトル”とし,その(複素)共役なベクトルを”共変ベクトル”とする事が,多いようです. #要するに,使い勝手が良く,概ね分かればいいわけです.
>繰り返しますと「反変ベクトル」という表現は「縦表示をベクトル」という立場での概念であり, >「縦表示をベクトル」という立場は高校から連なる考え方で今でも認められていますが, >個人的には古い考え方だと思います.
確かに,縦書きか横書きは,書道家でも迷うときがあると思います.
匿名でも,実名でも,対応可能な場合には,お気軽にご質問ください♪