乗積
乗積
G さんの書込 (2007/09/04(Tue) 19:37)
乗積 Product[Sqrt[(-1+Cos[(2*k*Pi)/n])^2+Sin[(2*k*Pi)/n]^2],{k,1,n-1}]=n の証明をお願いします.
食指を動かしていただき感謝します.再掲;
問1乗積 Product[Sqrt[(-1+Cos[(2*k*Pi)/n])^2+Sin[(2*k*Pi)/n]^2],{k,1,n-1}]=n の証明をお願いします!
問2 Abs[Product[E^((2*k*Pi*I)/n)-1,{k, 1, n - 1}]]=n の証明をお願い致します!
(問1と問2は同一ですので何れかのシンプルな証明をお願い致します!) 具体例は以下達です;
Re: 乗積
zoro さんのレス (2007/09/04(Tue) 23:15)
回答ではありませんが,和の公式は多いですが,積の公式は見慣れていないので,見やすく書いてみます.
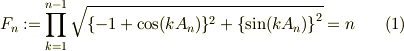
ここで, 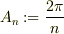
試しにすこし変形すると,
![F_n &= \prod_{k=1}^{n-1}[2\sin(k\alpha_n )]\\&= 2^{n-1}\prod_{k=1}^{n-1}\sin(k\alpha_n) \tag{2}](http://hooktail.maxwell.jp/bbslog/4aee637bd851b60e427a796865a15e11.png)
ここで, 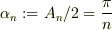
式(2)について,n=2..4 までは式(1)が成立するのは確認出来ますが,漸化式が成り立ちませんね.大きなnについて, 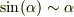 や
や 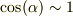 でごり押しして展開するのも嬉しくないですね.感じとしては積→和に持ち込むとか.
でごり押しして展開するのも嬉しくないですね.感じとしては積→和に持ち込むとか.
Re: 乗積
スパイク さんのレス (2007/09/05(Wed) 00:41)
三角関数を展開して帰納法を用いられましたでしょうか?
Re: 乗積
zoro さんのレス (2007/09/05(Wed) 03:51)
まだ解けていませんが,考え易くする為には,正弦で考えるより余弦で考える方が簡単そうなので,n=偶数に限るとして
![F_n &=\left[ \prod_{k=0}^{n/2 -1}\{2\cos(k\alpha_n )\} \right]^2 /2 \\&= 2^{n-1}\left[ \prod_{k=0}^{n/2 -1}\cos(k\alpha_n ) \right]^2 \tag{3}](http://hooktail.maxwell.jp/bbslog/340821731970ca9e9e81bdbf0a82c89e.png)
とすると三角関数が重複しなくなるので楽そうです.
スパイクさんの仰る「三角関数を展開して帰納法」とは,ド・モアブルの定理みたいな感じでしょうか.ついでにオイラーの公式を使って,楽出来ないでしょうかね.
Re: 乗積
スパイク さんのレス (2007/09/05(Wed) 04:23)
いつもお世話になっております.
ちょっと分かりにくかったかもしれません.すいません.
>ついでにオイラーの公式を使って,楽出来ないでしょうかね.
そうなんです.この手の問題は, 三角関数を自然数の分数和に展開しまして(指数関数と三角関数の関係を用いて), 正弦が奇関数であり,余弦が偶関数であることから, 乗積との可換性を用いて証明した事を覚えております. 肩の荷が下りるように,四則演算で済む利点があります.
#方向性は,似ている気がしますので, #zoroさんのやり方を拝見させていただこうかなと思いました(^^♪
Re: 乗積
zoro さんのレス (2007/09/05(Wed) 11:31)
スパイクさんのヒントから,少し進めると,
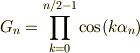
n=2,4,6までやって見ましたが,なにか予測と違っていてヘンテコリンな規則があるような,ないような.まだ出来ない....
不思議なのは,  を最後には計算しないと行けない筈だが,最後の最後に消えるのは不思議だ!,ですね.
を最後には計算しないと行けない筈だが,最後の最後に消えるのは不思議だ!,ですね.
Re: 乗積
zoro さんのレス (2007/09/05(Wed) 18:22)
n=8について,計算した所,Gnはルートnになりませんでしたが,Fnはnになりました.どうも,高次のnになると,cos(αn)は出ないで,kα=π/2 とかの値になって消えるもよう.
しかし,どう見ても一般的な漸化式を引き出せる様な感じではありません.従って,私の力では,残念ながらシンプルな解法を得るのは絶望的な気がします.もう少しトライしますが,識者の解説をお願いした方が良いと思います.
#残りの可能性は,自乗するときの二項定理を使った表現から漸化式が出るかもしれないと,淡い期待をしています.
とはいえ,このような数学的問題を,少しでも齧り付く事ができて面白かったです.自分は,高校生の頃,物理は面白くて独学しましたが,数学は道具と割り切って,覚えるだけで自分で解く楽しみを感じませんでした.
是非とも,このスレッドをご覧になったお若い読者の皆様方には,物理だけでなく,数学,いや少なくとも物理数学の面白さにも,目をやって頂きたいと思います.
【追伸】
数学の問題に手を出した原因がもう一つあります.今年の夏に結城さんというプログラマで作家の方が書いた「数学ガール」という本を拝見したのです.この歳で,この本を読んで,数学の面白さを知らされたようでした.数列と母関数といった関係はとても面白かったです.多分,学校の図書館には無いでしょうが,市民図書館辺でご覧になれると思います.
Re: 乗積
スパイク さんのレス (2007/09/05(Wed) 18:50)
こんばんは,
zoroさんへ
私の様な者が申し上げるのは,失礼かも判りませんが, あと少しのところへ来ておられるような気がします. #無理をなさらないことを願っております.
Gさんへ
誠に申し訳ないのですが,問い2の数式の表記に間違いはないでしょうか? #出来れば,宜しくご確認の程,お願い致します.
Re: 乗積
G さんのレス (2007/09/05(Wed) 19:32)
zoro 様スパイク様有難う御座います 面白かったと云っていただき, 心暖かいコメントをいただき,嬉しい♂喜しい.
n=8のとき;
問2の数式の表記に間違いはありません. n = 17; で確認の顛末; Abs[Product[E^((2*k*Pi*I)/n)-1,{k, 1, n - 1}]]=17
Abs は
です
Re: 乗積
クロメル さんのレス (2007/09/05(Wed) 23:20)
院試終わってからの初書き込みです.
これは,なつかしい. 僕が大学受験するとき,有名な問題(パズル?)だったと思います. キツネにつままれたような気分になる証明法を知ってますよ^^
Gさんは,お時間ありますか? zoroさんが,解いている最中のようなので, いきなり,解答をだしたら,空気読めと言われそうですので, ちょっと待とうかなと…(^^;
スパイクさんの知っておられる答えとは,違うようなので, あとでスパイクさんの解答も聞きてみたいです.
P.S.「数学ガール」は面白かったですか.小説なのに,本屋で理工学書のところに置いてあり,印象に残ってます.今度,買ってみようかな?
Re: 乗積
G さんのレス (2007/09/06(Thu) 01:20)
時間は∃します
(昼は毎日遊泳その他は暗なこと坤なことで....)
Πr=1n-1sin(πr/n) = _________<−−−隠匿. (E. W. Hobson, A Treatise on Plane & Advanced Trigonometry, 7th ed., Dover, New York. §90 & §188.)
そうでしたかァ
(過去形のみでさみしい惨頭苛)
E. W. Hobson, A Treatise on Plane & Advanced Trigonometry の 検索結果 約 654 件
Re: 乗積
zoro さんのレス (2007/09/06(Thu) 07:49)
どうも,複素数円の図形を見ながら式を書いていて, 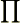 を見ながらも,積の順番を好きにして良いのを忘れていました(爆笑).
を見ながらも,積の順番を好きにして良いのを忘れていました(爆笑).
で,これまでの書き方の都合上,Gnで考えますと,角度0の余弦は1なので,何となく除外するのは恐れ多いと思っていましたが,積なのでドライに除外します.そして,
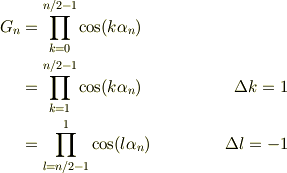
そうです,積の自乗を作れば良いので,積の組み合わせは「好きにしていい」訳ですから,kをランニング・パラメータとすれば,対応するlは,
◆急用の為に中断.申し訳ありません.
〜〜〜 【追伸】
クロメルさん,復帰おめでとうございます.
是非とも別解をお教え下さい.この手の問題は,複数の解がある方が面白いですから.
Re: 乗積
Re: 乗積
スパイク さんのレス (2007/09/06(Thu) 09:37)
おはよう御座います. No.17779の方法が一番早かった気がします.
Re: 乗積
Re: 乗積
クロメル さんのレス (2007/09/06(Thu) 13:57)
zoroさんから,Goサインが出たようなので書きますね.
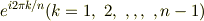
は,1のn乗根,つまり, 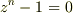 の1以外の解です.
の1以外の解です.
よって,因数分解できます.
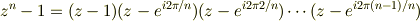
ここから因数  を除いた残りの部分を
を除いた残りの部分を 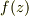 と置きます.
つまり,
と置きます.
つまり,
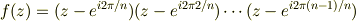
確認しておくと,いま求めたいのは 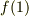 の値です.
の値です.
一方,
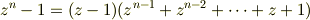
という風に,因数分解できますよね. もうお気づきになりましたか?
ここから,
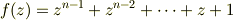
になりますよね.
この多項式において,z=1としたもの(または,その絶対値をとったもの)が解になります.
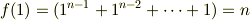
証明終わり.
P.S. 僕はこの解法にしばらく納得いきませんでした.シンプルすぎて肩すかしをくらったような気分になったのを覚えています^^
でも,みなさんの導きだした解答が,よく分かりません.
ここの二つ目のイコールって何で成り立つのでしょうか? こんな公式ありましたっけ?
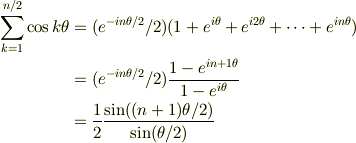
に似ているなあとは思ったのですが.
Re: 乗積
スパイク さんのレス (2007/09/06(Thu) 16:24)
クロメルさん,回答有難う御座います.
結構有名な問題で,当時,答えを知っている上で,出されている気がしました(^^♪
>ここの二つ目のイコールって何で成り立つのでしょうか? >こんな公式ありましたっけ?
>に似ているなあとは思ったのですが.
今,頭の中で確認したところ,合うようですね. 公式としては,あったと思います. #岩波の数学公式集辺りに掲載されていませんでしょうか?
Re: 乗積
Re: 乗積
クロメル さんのレス (2007/09/06(Thu) 18:38)
なるほど,確かにそういう公式があるのですね. 導出法までは分からないのが残念ですけど.
しかし,このサイトは,便利そうですね. 以後,僕も使わせてもらいます:)
Re: 乗積
G さんのレス (2007/09/06(Thu) 20:08)
Eric W. Weisstein の検索結果 約 307,000 件 【叡知・叡智・英知】の【結集】だと感謝し,覗かない日は在りません. mathematicaのnbも超有用ですから Http://www.ericweisstein.com/
Http://mathworld.wolfram.com/about/ MathWorldに関して MathWorldTMウォルフラム研究,Mathematicaのメーカーによって無料サービスとして世界の教育および教育のアウトリーチに対する関与の一部としての数学およびインターネット・コミュニティーに供給されて,ウェブの最も広範囲な数学的な資源です......
MathWorldは,何千もの寄稿家からの援助を持ったエリックW.Weissteinによって10年間以上にわたり組み立てられました.その内容が最初に1995年においてオンラインに見えて以来,MathWorldは,数学および教育のコミュニティーの両方の数学的な情報のnexusとして出現しました......
Re: 乗積
クロメル さんのレス (2007/09/06(Thu) 21:30)
>スパイクさん
>結構有名な問題で,当時,答えを知っている上で,出されている気がしました
すいません,答えを知っているの主語が分かりません(;A;)
岩波の公式集ですね,今度図書館などで見てみようと思います. マグロウヒルの公式集は持っているのですが,あれでは公式の羅列なので, 導出方法は分かりませんね.
>Gさん
情報ありがとうございます.やはり有用なサイトは世界の共通言語,英語のサイトなんですね.数千の寄稿家,十年以上…日本とは規模が違う感じですね.(日本の物理の記事投稿サイトのメンバーの僕が言うのは,問題発言かもしれませんね(^^;)
Re: 乗積
スパイク さんのレス (2007/09/06(Thu) 23:17)
クロメルさんへ
>>結構有名な問題で,当時,答えを知っている上で,出されている気がしました
>すいません,答えを知っているの主語が分かりません(;A;)
いえ,こちらこそ,至らぬ点が多々あるかとm(__)m 学生当時,”教官”に問題の解法(答え)を紹介していただけるのは大変に有難かった上に,感心したのですが, 背景までご紹介される方は,なかなか少なかった記憶がありまして. #お蔭様で,久しぶりに醍醐味を味わった気が致します.
>岩波の公式集ですね,今度図書館などで見てみようと思います. >マグロウヒルの公式集は持っているのですが,あれでは公式の羅列なので, >導出方法は分かりませんね.
岩波の公式集は,戦後の復興に貢献された上に,利用頻度から,誤植が少ない 事で知られているようです. 但し,証明はマグロウヒルの公式集同様に記載されては居なかったかと思われます. 私の場合には,そのまま引用するのではなく,なるべく確認もしくは証明した上で, 利用するようにしておりました. #慣れると,数式を見た時点で,概要が掴めるようになった?気が致しております.
あくまで蛇足ですが,実務においては,資料なども完備しているとは限らないため, 周りと相談しつつも,結局は自分なりに切磋琢磨しなければ,鈍ってしまうのだな, という事を痛感することが多いんです. #経験と勘が試されることが多くなるようで(^^♪
Re: 乗積
zoro さんのレス (2007/09/06(Thu) 23:56)
Gさん,スパイクさん,
まだノートと睨めっこの状態ですが,ブレイク出来てません.
ただ同道巡って,
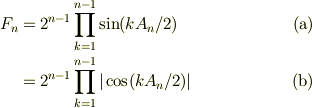
これらの変形で,定数項を引き出しながら,三角関数部分が消滅する要に出来たらと思いましたが成功しませんでした.今しばらく,保留して,再検討します.
で,数学の問題をこんなに長い事考えた事は,産まれて始めての事です.疲れたものの,此れがあって,z^n=1 の解法の凄さが身に沁みます.
クロメルさん,
「絶対値を取る」と思い至りませんでした.タッチのさで運命の女神に見放されましたが,この方法から,逆に上の式を誘導することを,すこしショックから抜け出たら考えて見ます.
Re: 乗積
スパイク さんのレス (2007/09/07(Fri) 04:27)
zoroさんへ
了解いたしました. 初め,真っ向から向かわれたときには,若干心配しましたが, 同時に感心致しておりました. #zoroさんの意思を尊重したいかと思います.
Re: 乗積
zoro さんのレス (2007/09/07(Fri) 10:22)
スパイクさん,ご助言を下さり有り難うございました.
残念な事に,まだ回答を得ていませんが,長丁場で考えて行きます.
他方,この手の証明問題は複数の解法があると,初学者の理解空間の拡張に効果的だと思います.若し宜しければ,解法をお教え下さればと思います.
数学と物理は,なにか判りませんが「似ていて非なる」ところがあると思います.巧く言えないのですが,このような証明問題一つでも,小さな数学空間を構成するように感じます.
他方,物理では,連綿とした問題の中の一部を理解して行く様な感じです.なかなか,別解を比較して論じる事は出来にくいようです.逆に,数学の事例で,別解を並行的に論じられるのを拝見すると,物理での事例考察にも参考になるような気がします.
「このような世界に指を染める勇気を持続できた助言」を頂けました事を,改めて感謝いたします.
Re: 乗積
G さんのレス (2007/09/07(Fri) 10:23)
zoroさんへ
「半径1の円に内接する正n角形の一頂点から他の全ての頂点にひいた線分の長さの積はnになる」 ということを証明したいのですが…
外接円を原点中心の単位円とし一頂点A0を(1,0)にとります. また円上に反時計回りに等間隔にA1,A2,…,A(n-1)をとります. このとき余弦定理から (A0Akの長さ)^2=1+1-2*1*1*cos(2π/n) =2-2cos(2π/n)=4sin^2(π/n) ゆえ求める積は Π[k=1〜n-1]2sin(π/n)
と【変形したところで行き詰ってしまいました】 どのようにすれば証明できるでしょうか. 質問投稿日時:07/03/24 22:34 と同地点で!【熟考してみます I will think it over carefully】 なる方 に 漂着いたしました.
回答 見付けたので貼っておこう. 直接的な証明は思い付かんかった. とても参考になりました.ありがとうございます. 証明が技巧的で面白いですね. なる応答在り(暫く貼られた参考URLを隠匿します(スミマセン))
再掲;
の (22)
(22)を余罪CoSin にかえたら如何!在りそうでない;
余罪CoSin にかえたのがないので 戯れに求めると面白い!
Re: 乗積
スパイク さんのレス (2007/09/07(Fri) 18:50)
GOサインが出たようですので, 記述させていただきますね. 気になる箇所がありました.
exp(?n)=Πexp(n)n∈C
が成立すると・・・? #上の表式間違えていますかね...
Re: 乗積
G さんのレス (2007/09/07(Fri) 20:01)
http://mathworld.wolfram.com/ExponentialFunction.html
の(2)exp[z1+z2+....+zn]=exp[z1]*exp[z2]*.....*exp[zn] のことと判読しOKです.
Re: 乗積
G さんのレス (2007/09/07(Fri) 21:16)
問2 Abs[Product[E^((2*k*Pi*I)/n)-1,{k, 1, n - 1}]]=n
<------------------- 引く1が在るのです. n=17ならば {-1 + E^((2*I*Pi)/17), -1 + E^((4*I*Pi)/17), -1 + E^((6*I*Pi)/17), -1 + E^((8*I*Pi)/17), -1 + E^((10*I*Pi)/17), -1 + E^((12*I*Pi)/17), -1 + E^((14*I*Pi)/17), -1 + E^((16*I*Pi)/17), -1 + E^(-((16*I*Pi)/17)), -1 + E^(-((14*I*Pi)/17)), -1 + E^(-((12*I*Pi)/17)), -1 + E^(-((10*I*Pi)/17)), -1 + E^(-((8*I*Pi)/17)), -1 + E^(-((6*I*Pi)/17)), -1 + E^(-((4*I*Pi)/17)), -1 + E^(-((2*I*Pi)/17))} の積なのです.
S^(2-1)上の点Pk ,P1=(1,0) でvector P1Pk を複素数表示したものがE^((2*k*Pi*I)/n)-1なのです.
(もし命題が偽を示すのが目的なら Abs[Product[E^((2*k*Pi*I)/n)-1,{k, 1, n - 1}]]=n とならぬ一例のnを俎上にすればよい)
▽命題が真を示すのが目的なら Table[Abs[Product[E^((2*k*Pi*I)/n) - 1, {k, 1, n - 1}]] = n, {n, 5, 19}]
={5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19} と幾ら具体例達で確証しても証明とは判断されぬ
- 非情な世界なのです.
- 嗚呼..
Re: 乗積
G さんのレス (2007/09/07(Fri) 22:33)
早とちりしておりましたら御免なさい
真摯な気持ちで私「待つわ」別解の導出を(有難う御座います)
重ね重ね;
真摯な気持ちで私「待つわ!^(2007+___)」
Re: 乗積
スパイク さんのレス (2007/09/07(Fri) 23:48)
Gさん,ぜーんぜーん心配しなくても大丈夫ですよ. いつも,こういった案件ばかりですから(^^♪ どうも,条件が定まってきました. 取り敢えず,ご検討くだされば,幸いです. #宜しかったら,一緒にやりません?
Re: 乗積
スパイク さんのレス (2007/09/08(Sat) 01:22)
追補です.
どうやら,正則関数f,gにおいて,
Πf(n)=g(?n)n∈C
が成立する場合,f(n)が解を持つときに, 左辺と右辺が解析的に接続出来る事を証明出来るようです. #本問においては,もちろんクロメルさんの解法で問題ないです(^^♪ #一般的に拡張するとどうなるかなと思いまして. #もっと,もっと?
Re: 乗積
zoro さんのレス (2007/09/13(Thu) 15:24)
Gさん,もう見ていないかもしれませんが,すこし自分の考えを述べてみます.
少なくとも,自分の実力では,三角関数の変形から,常数nを引き出せませんでした.自分としては,Z^n=1 の方程式にまつわる関係式からのみ「n」が出るだろうと感じます.
従って,根の関係式を,さわったもののz=1以外の根の積をとり,z=1での絶対値とするクロメルさんご紹介の式しか判りませんでした.
で,この方式を,すこし変形する方法を作って見ましたので,下記にご説明します.
#数学ガールに書いてあったようですが,「テトラちゃん流の,こまったら微分してみる!」に従って見ました.
〜〜〜
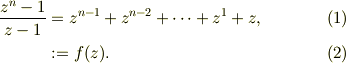
他方, 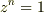 の原始根
の原始根 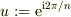 とすると,式(2)は因数分解できる;
とすると,式(2)は因数分解できる;
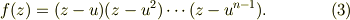
また,式(1)の分母を払い;
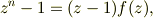
として,辺々をzで微分すると;
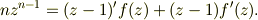
ここで 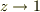 を考えると;
を考えると;
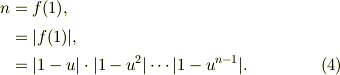
以降はクロメルさんの筋書きで,QED.
Re: 乗積
スパイク さんのレス (2007/09/13(Thu) 18:54)
zoroさんへ,
とうとう,正解に辿り着かれたようで,賛辞を申し上げたいかと存じ上げます. いわゆる定石(棋譜)のようなものはあっても,結論に至る道筋は, 一通りではないことから,生きた数学を感じました(^^♪
Re: 乗積
G さんのレス (2007/09/13(Thu) 19:56)
zoroさんへ,
Z^n=1 の方程式にまつわる関係式からのみ「n」が出るだろう とのこと,いいえ問1問2は独立に証明可能です.
三角関数の変形から,常数nを引き出す発想例えば;
Re: 乗積
zoro さんのレス (2007/09/13(Thu) 21:07)
皆さん,
ううむ,ガンマ関数で正弦関数が表現出来るとは....
>三角関数の変形から,常数nを引き出す発想例えば; > http://b4.spline.tv/study777/?command=GRPVIEW&num=344
後々の為に,一部を式に書いてみましょう(式の意味は追えませんが);
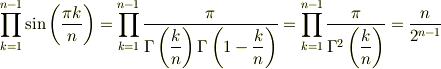
で,「sin ガンマ関数」を検索したら,
・級数と乗積
というサイトにであいました.
特殊関数は苦手なので,ボチボチと調べてみます.
数学の得意な方で別解をご存知でしたら,書き込んで頂けると面白いですね.
Re: 乗積
スパイク さんのレス (2007/09/14(Fri) 01:05)
どうも,
>数学の得意な方で別解をご存知でしたら,書き込んで頂けると面白いですね.
リンク先:
>数理科学のページ >物理と数学のハイレベルな記事が並びます.
この手は,結構身近にあることが多いので,見守る方針を採っておりました(*^^)v
Re: 乗積
zoro さんのレス (2007/09/15(Sat) 15:31)
スパイクさん,
>>数理科学のページ
あ,こんな雑誌,...,全く忘れていました.「SGCライブラリ」には時々お世話になっていますが,サイトにはお邪魔してませんでした.きっと,後,数年位したら,見に行く様な気がします.ご教示,感謝します.