面積分の計算です．

やまさんの書込 (2007/09/03(Mon) 16:19)

はじめて，書き込みさせていただきます．

面積分の計算についての質問なのですが，

U={(x,y,z)∈R^3|x^2+y^2+z^2=r^2,z≧0},r>0とする．

n(x,y,x)=(1/r)(x,y,z)を外向き単位法ベクトル場とし， a(x,y,z)=(1,1,1)とする．この時，面積分

∫a・nds の値を求めよという問題なのですが，どのように式変形して解いたらよいのか分からなく困っています．

どなたか宜しくお願いいたします．

やまさん，初めまして．

この場合，面の領域は半径rの球の上半分の表面だけですか？z=0の底面は積分に入るのでしょうか？

いずれにしろ，面積分を体積分に置き換えると，計算が端折れる気がしますが．

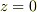たぶん， z=0 の面はふくまないでしょう(理由は消去しました)．でも仮想的に 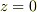z=0 を含めて考えるとzoroさんのおっしゃるとおり簡単に解けますね．

n=(n_1,n_2,n_3)とすると，

∫a・nds=∫(n_1+n_2+n_3)ds =∬(0+0+0)dxdydz =0 でよいのでしょうか？？

体積分としては，上半分の半球部分に取る訳ですよね．で発散がゼロだから体積分からの寄与はゼロ．

他方，半球部分の面積分は，２つの部分の和；（１）興味のある上半分の半球の表面部分（２）ｚ＝０の円の表面の部分この部分の微小面積要素の方向は-zの方向ですよね．あ，...．

体積分と合わせれば，（１）＋（２）＝０でしょ．

〜〜〜もう少し，遡って考えれば良かったかも知れません，反省．

ありがとうございました．