俊一 さんの書込 (2007/08/25(Sat) 01:29)

エネルギー等配分則は，他の法則から，説明することができるのでしょうか？ 例えば，単原子分子の場合であれば，速度の成分の二乗平均は，マクロ的にみれば対称であることから理解できます． しかし，２原子分子の場合には，このような説明はあるのでしょうか？ ぼくのもつ本では，エネルギー等配分則を用いて，比熱をもとめています． 回転の一つの自由度ののエネルギーの平均値が重心の運動エネルギーの一つの自由度の平均値と同じ大きさになる理由は，エネルギー当配分則なしで説明することはできないのでしょうか？

ぼくは，応用物理学科を卒業し，修士までいっています．参考文献などを示して頂いてもありがたいです． それとも，エネルギー等配分則は原理でありほかの何からも導くことは出来ないものなのでしょうか？ ぼくの理解では，エネルギー保存則のように，一般的には証明できないが，個別には説明できるものも多いではないかと考えています． いかがでしょうか？

zoro さんのレス (2007/08/25(Sat) 03:31)

俊一さん，初めまして．

昔の記憶で書いているので，詳しい方が書かれるまでの参考に見て下さい．

２原子分子の場合は； ・重心系の並進自由度：３成分 ・相対運動についての運動； ・相対振動の自由度：1成分 ・相対回転の自由度：1成分←注記） 注記）相対座標を回転軸とする回転は， 対称的な分布のために量子力学的に禁止． と考えて，全部で，5成分の自由度となったように考えるとか．

相対振動の結合力が弱ければ，基本振動以外の振動準位を考えたり，分裂が出て来たりで，複雑な挙動が在り得るのでしょうね．

俊一 さんのレス (2007/08/25(Sat) 07:56)

ZOROさんありがとうございます． ぼくの書き方がよくなくて誤解をまねいたようです． ごめんなさい． 僕の疑問は ＞２原子分子の場合は； ・重心系の並進自由度：３成分 ・相対運動についての運動； ・相対振動の自由度：1成分 ・相対回転の自由度：1成分

これらのそれぞれの自由度ごとの平均エネルギーがなぜ等しいといえるかという疑問です． ・重心系の並進自由度：３成分が，等しいのは納得できます． しかし，それと他の２つの平均エネルギーが同じになる理由がわからないのです．

wikipwdiaには エネルギー等配分の法則は，エネルギーεが上の式で示されるように二次の形式で表現できる時に成り立つ（調和近似が成り立つ場合も含まれる）．系において，量子力学的な効果が顕著となる場合や，非調和項が無視できない場合は，この法則は成立しなくなる． と書いてあります．

この文面からだと，統計力学から導けるようにも読めてしまいます．どうなのでしょうか？２分子が剛体でつながれている場合には，等配分されることを計算で導くことができるのでしょうか？

佑弥 さんのレス (2007/08/25(Sat) 10:18)

はじめまして．

等エネルギー分配法則は，統計力学を用いれば，次のような議論で導出する ことができます．

僕自身は量子論的な効果があらわにみられる場合を除けば，n自由 度系のエネルギーが 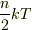になることから1自由度 あたりに 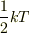のエネルギーをもつと解釈するという 議論をして導いたことがあります．

これでは，実際に等分配なのかどうかは分からないという議論もあり得る とは思うのですが，直接的に同じエネルギーをもつのかを議論したことが ないので，これ以上のことは僕には分かりませんが，基本的に知りたいのは 全エネルギーだと思うので，上のような議論で十分なのだろうと思います．

zoro さんのレス (2007/08/25(Sat) 14:40)

私は，分子運動論から先が判らなくて落ちこぼれたので，詳しい事は判りません．

でも，大雑把にいえば，分子運動論の段階で，希ガスのような単一原子ガスでは，3/2kTが比熱を良く表し，水素ガスのような2原子分子ガスでは，5/2kTが良く合いそうと言う事実から，分子運動の1自由度あたりに1/2kTが割り振られるという，奇麗な形が得られたのだと思います．

ところが，複雑な分子になると，単純なモデルでは段々に合わなくなるように思いました．一般論としても，分子系をハミルトン形式で与えた時に，すでに何らかのモデルが介入し，さらに熱平衡の処理をする時に，ポテンシャルエネルギーに仮定をする要なきがします．佑弥さんがされた計算を公開されると解り易いようにも思います，ないしは何らかの図書にあれば，それをお教え下さると嬉しいです．

くだくだ書きましてが，エネルギ等分配の法則とは，そんなに厳密なものでは無いと思います．でも，簡単な論議をする上では，とてもイメージし易い考え方ですよね．

ｋｏｍａｇａｔａｋｅ さんのレス (2007/08/25(Sat) 20:52)

エネルギー等配分則は比熱を結びつけて考えられています． この場合の比熱はモル比熱でないといけません．１つ１つの粒子についてエネルギーを考えるからです． ところが物理の教科書を見ると固体比熱はＪ／ｇ，ｃａｌ／ｇででています．気体比熱で初めてモル比熱Ｊ／ｍｏｌが出てきます．比熱の取り扱いの立場は一貫性がありません．実用上の立場と物質の性質を共通性で見ていこうという立場とが混ざっています． 今までに書かれている返信でもエネルギー等配分則は不活性元素気体の３Ｒ／２が出発点であるかのように書かれています．固体におけるエネルギー等配分則はどうなのかが問題になっていません． 私が初めてエネルギー等配分則を知ったのは３回生の時に読んでいた朝永の量子力学でした．ポテンシャルの場の中で振動している原子の場合，運動エネルギーの平均値と位置エネルギーの平均値が等しくなるという内容でした．そこでデュロン・プティの法則という名前を知りました．金属の比熱は成分元素の種類によらず１ｍｏｌ当たり３Ｒになるというものです．１８１９年です．不活性元素が発見されるよりもずっと前の話です．エネルギーが二乗項で書けるというのは運動エネルギーと位置エネルギーの表現から来たものです． 理科年表に単体のモル比熱の表があります． 常温（１５℃）での比熱は金属の場合，ほぼ２４〜２６Ｊ／Ｋ・ｍｏｌです． Ｒ＝８．３Ｊ／Ｋ・ｍｏｌで考えると３Ｒ＝２４．９になりますからまあまあでしょう．でも普通よく書かれているようなｇ当たりの比熱の印象とはまるで違います．元素の種類によってはかなりのズレが見られます．デバイの特性温度でスケイルする必要があるのだと思います．ポテンシャルの部分が調和振動子の２次の形式からずれてくるのかもしれません．

２原子分子の場合，並進の自由度の３と回転の自由度の２で合わせて５という表現をします．定積比熱は５Ｒ／２です．亜鈴型の剛体モデルですね．剛体モデルということは原子間距離が変わらないということですから伸縮振動が励起されていないということになります． ３原子分子の場合，自由度７にします．２つの原子間距離が変わらないということになります．変角振動は起こっていることになりますが分子によって程度の違いがあるでしょう． 水Ｈ２Ｏの場合，変角振動で１５９５／ｃｍ，対称伸縮振動３６５７／ｃｍ，逆対称伸縮振動３７５６／ｃｍです．全て赤外領域ですが変角振動の方が励起されやすいことは分かります．

エネルギー等配分則は熱エネルギーにより励起されるエネルギー順位を考えているはずです．常温で十分に励起されるような順位の自由度であれば加えた分だけのエネルギーを吸収するということだろうと思います．

昔もそれほど分かっていたというわけではありませんのでこの程度までです．間違っているかもしれません．

佑弥 さんのレス (2007/08/25(Sat) 21:26)

僕がすぐに思いつける導出方法は次のようにやります．おそらく古典統計と カノニカル分布を使うのが一番簡単と思います．

n自由度系のハミルトニアンは一般運動量 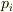と適当な係数 <m_i> (質量とか慣性モーメントなどをまとめてこのように表しておきます．)を用いて

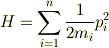
と書けます．(ポテンシャルエネルギーがない場合を考えることにします．)

このとき，系の分配函数は

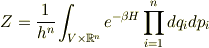
となります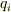．( と 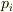が互いに共役な座標と運動量と してください．)Vというのは一般化座標の積分区間だとしておきます．

このとき

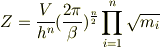
となりますから，系のエネルギーEは

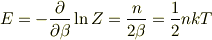
となります．

ここではポテンシャルはないものとしましたが，調和振動子型のポテンシャルなら 一つの調和振動し当たり 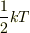のエネルギーが振られることが同様に分かります．おそらく多分子の気体など複雑な系になると，その他の項が無視できない影響を持つために等分配則からずれてくるのだと思います．

佑弥 さんのレス (2007/08/25(Sat) 22:31)

図書について書き忘れました．

等分配則に関する記述があるもので，僕が持っている統計力学の本は 次の2冊です．

岩波基礎物理学シリーズ7巻統計力学長岡洋介著

大学演習熱学・統計力学久保亮五編

ほかに僕が持っている統計力学の本は

Statistical Physics 吉岡大二郎著

ですが，等分配則がかかれていたかどうかは覚えてません． (もちろんカノニカル分布等には分かりやすい説明があるので 後は自分で導けるようになりますから，どの本を読んでも いいとおもいます．)

俊一 さんのレス (2007/08/25(Sat) 23:59)

ありがとうございます 僕が求めていた答えは，佑弥さんのものだと思います．

ぼくももっている本を調べていたら．

岩波書店物理テキストシリーズ 統計物理学（中村伝） のｐ１０８に同様のものがありました． これから細かく読んでみます．

＞エネルギ等分配の法則とは，そんなに厳密なものでは無いと思います． というご意見もありますが， それは，物質をどう理想化して考えるかということで， たとえば２分子原子を剛体として扱えば，正しいと考えています．

確かに物理の中には，摩擦係数や，はねかえり係数，のように 厳密なものでないものもありますが，法則と名の付くもので そのようなものは思いつきません．

ただ，ぼくも熱力学，統計力学の分野の法則はいまひとつ掴みかねています． 統計力学は，理論よりも物性への応用に触れる機会ばかりが多く理論を追うような授業は多くないと思います． ただ，やはり理想化された単純化された範囲では厳密に成り立つと考えてよいと考えています．

もうすこし勉強してみます．ありがとうございました．

ｋｏｍａｇａｔａｋｅ さんのレス (2007/08/26(Sun) 12:38)

法則について「厳密に成り立つ」とか「成り立たない」とかの言葉使いが出てきています．「正しい」とか「正しくない」という表現も出てきています． これについて私はちょっと馴染めないものを感じます．

それは多分物理の法則が力学の法則であったり，電磁気の法則であったりするからでしょう．そこには物質の多様性は出てきていません．

物性に関する法則（化学の法則も全てここに含まれるでしょう）というのは多様性の中に成り立つ共通性のようなものです．おおむね当てはまるというものです．その性質が何故成り立つのかということから物質の性質の一端が明らかになっていくというものです．「厳密に」という言葉で考えることはあまり意味を持たないものだと感じています． 「厳密に」ということにこだわれば実体よりもモデルが優先するという事が起こってしまいます．あるモデルで考えた場合にそれから導かれた結果がモデルと矛盾しないというのは当然のことです．その意味では俊一さんの

＞やはり理想化された単純化された範囲では厳密に成り立つと考えてよいと考えています

は当然のことで同語反復に近いと思います．

＞たとえば２分子原子を剛体として扱えば，正しいと考えています．

これもモデルと結果が矛盾しないということを言っているだけで法則が正しいとか正しくないとかではないのです．

問題になるとしたら２原子分子の剛体モデルが当てはまる分子がどれだけあるか，その成り立つ条件はどういうものか，そこから何が見えてくるのかだろうと思います． 当てはまる範囲の広い法則と狭い法則がありますが厳密であるかどうかとは無関係のことだと思います．当てはまる範囲が狭ければ正しくないということでもありません．（こういう言い方自体，物理で考えておられる「法則」とは違うということになりそうですね．） ※良く当てはまっても根拠がないというのは「法則」とは言えないでしょう．そういうのに対して「正しくない」という言葉使いは意味を持つでしょう．根拠が見つからない法則の中で有名なものは「ボーデの法則」です． ※教育実習に来て状態方程式は間違っていると言う学生が時々います．「不充分である」，「当てはまらない領域がある」ということは間違っているということではないと注意するのですがピンと来ていない様です．そういう学生はヴァン・デル・ワールスの式が正しいと言います．「その式も当てはまらない領域があるでしょう」，「近似を上げただけでしょう」と言うと途方に暮れた顔になります．

高校で出てくる気体の法則（ボイルの法則，シャルルの法則，アボガドロの法則，分圧の法則，・・・），浸透圧の法則等は全て物性的な法則です．

俊一さんが引用しておられるｗｉｋｉの文章に

「量子力学的な効果が顕著となる場合や，非調和項が無視できない場合は，この法則は成立しなくなる．」とあります．

「量子力学的な効果が顕著になる」とはエネルギー順位が大きくて熱励起が十分に起こらないという場面でしょう． 「非調和項が無視できない」とは熱励起は十分に起こってもエネルギーの表現が違ってくるということでしょう． ２原子分子で言うと並進も回転も古典的に扱うことが出来るでしょうから振動の部分が量子力学的なものになります．剛体として扱えるというのは熱励起が起こっていないということですから振動のエネルギー順位が熱エネルギーに比べて大きいということになります．

水素で見てみましょう．理科年表には定圧比熱とγが載っています． ０℃２８．６Ｊ／Ｋ・ｍｏｌγ＝１，４１０ １００℃２８．９１．４０４ ４００℃２９．８１．３９

剛体モデルの等配分則だと７Ｒ／２＝２９．１γ＝１．４です．合うのは１００℃より少し上だと言うことになります．でもこのズレが量子効果なのか非調和項なのかは分かりません．（多分非調和項でしょう．） でも正しいとか正しくないとかではない話です．

塩素で見てみましょう． ２９８．１５Ｋ３３．８Ｊ／Ｋ・ｍｏｌ ４００Ｋ３５．３ ６００Ｋ３６．６

これはむしろ９Ｒ／２＝３７．６に近い値です．自由度９ということは２つの自由な原子ということですから（この部分は間違いです．後ろに訂正があります．）原子間の伸縮振動がかなり励起されているということになります．ハロゲンの反応性は熱や光で解離しやすいという性質から来ているということとつながってきます．

比熱には物質を構成する粒子の挙動，環境が反映します．物性研究の有力な手段になります．

４０年以上物理と化学にまたがった領域にいましたので物理オンリーの人達とは感じ方が違うのかもしれません．

訂正すみません勘違いをしていました．

塩素の比熱は 自由度５の時Ｃｖ＝５Ｒ／２，Ｃｐ＝７Ｒ／２ 自由度６の時Ｃｖ＝６Ｒ／２，Ｃｐ＝８Ｒ／２（９Ｒ／２はあり得ません．）

Ｃｐ＝４Ｒ＝３３．２ですから伸縮振動が励起されていることになります．温度を上げると値が大きくなっていることは非調和項が大きく効いています．原子間距離が大きくなる方向に変化が起こっているはずです．

佑弥 さんのレス (2007/08/26(Sun) 16:47)

いえ，確かに法則が厳密に成り立つというのは，多少違和感が ありますね．

全ての(物理)法則には適用範囲というものがありますから，その 適用限界を超えて法則を使うことは難しいでしょう．実際に実験 してみると，理論値との間にずれが生じてくるのは避けられない と思います．それは，法則が正しいとか正しくないとかではなく て，適用範囲を使う人が間違っただけなのだと思います． ここで，ずれる原因を考えることで逆に色々なことが分かると思う のですが，これはkomagatakeさんが比熱の例に説明してくださった とおりですね．とても面白いと思いました．

今回の議論を例にとることにすると，エネルギー等分配則は (i)量子的な効果が無視できる条件にあること (ii)ポテンシャルが調和振動子の形をしていること を仮定として導きましたから，この仮定が満たされなければ 実測値から理論値がずれるのは当然ですね．

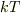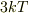例えば，金属の比熱も古典統計を使って等分配則から導こうと すると，適用範囲を超えた議論になってしまいます． 金属は原子の振動が1原子あたり3方向ありますから3つの振動子 を持ちますので，1振動子当たり のエネルギーを振ることで 形式的に のエネルギーを持つことが導けますが，純粋に古典 統計を適用して，等分配則を用いると，1原子あたり1つの自由電 子を放出すると考えれば 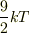となってしまいます． これは，電子の質量が非常に小さいために，常温では自由電子の 自由度は凍結してしまっているので，そこにはエネルギーを振り ません．つまり，(i)の条件を破っているのですね．

ｋｏｍａｇａｔａｋｅ さんのレス (2007/08/26(Sun) 17:44)

金属の比熱は格子比熱と電子比熱の合わさったものです． この様な２つの内容があるということは等配分という考え方があるからわかることだと思います． モル比熱が３Ｒなのか９Ｒ／２なのかという問題設定があって初めて実測と対比する焦点が定まることになります．実測は３Ｒの方です．その場合，３Ｒからの多少のずれは問題になりません．格子比熱と電子比熱は分離されている，常温では電子比熱は凍結されているという大きな結論が得られます．こういうのも法則の持つ意味だろうと思っています．

法則と実測値とが合わなくなったときに 法則の成り立つための条件が満たされていないというのは明らかなんですが 「合わなくなった」でそのまま終わりになる場合と 「合わなくなったからには合わなくなっただけの理由があるはずだ」という新たな追求が始まる場合があります． 後者の場合の法則は基準の設定のような働きをします．ずれが生じたら間違いであるというのではなくてズレは新しいことを見つけていく手がかりだということになります．私が書いた例で言うと剛体モデルが破れたら法則が破綻したというのではなく振動が励起しているということから原子の結合に対する情報が得られると考えるのです．

固体の格子比熱に限ってもあちこちでズレがでることがあります．２次の相転移に伴う比熱異常はそういう場合の例だと思います． 磁気相転移でも格子の相転移でも電気的な相転移でも比熱には全て引っかかってきます．まず比熱で当たりを着けてからそれぞれに固有の方法で調べるというのがよくやられています．

yama さんのレス (2007/08/26(Sun) 19:00)

塩素分子の定圧比熱が高温で7R/2からずれるのは，komagatakeさんのおっしゃる通り振動が励起されているためだと思いますが，この場合，高温になるほど励起される確率が大きくなることで比熱の増加は説明できるので，非調和項の影響はあるとしてもあまり大きくないと思います． 7R/2からのずれが水素原子より大きいのは，分子の質量が大きいので分子の振動数が小さくなって励起されやすくなるためでしょう． また，ハロゲンの反応性は，単体の分子が解離しやすいかどうかにも関係するとは思いますが，それよりも電気陰性度の大きさなど原子自身の性質によるところが大きいのではないでしょうか．

ｋｏｍａｇａｔａｋｅ さんのレス (2007/08/26(Sun) 19:55)

塩素の比熱の値を見ると７Ｒ／２からずれたと言うよりは４Ｒであるという方がいいのではと思って書きました．１５℃ですでに４Ｒを越えています．等配分で考えた値を超えているというのはその自由度は既に十分励起されているということだと思います．部分的に励起されている（確率的に励起されている）ということであれば４Ｒよりも小さくなります． 調和振動の範囲であれば既に励起されているものがもっと励起されても比熱としては変化しません．温度によって比熱が大きくなるということはポテンシャルの形が放物線からずれて非対称になっている事によると思いました．そしてずるずると原子間距離が大きくなるという結果になるのではと推測しました．

ハロゲンはラディカルを生成しやすいという性質があります．それが反応性に結びついています．電気陰性度はポーリングの値で言うと酸素と同じです．酸素原子の方が小さいので陰性度の影響は酸素の方で強く出ます．水素結合をする元素として酸素，窒素，フッ素が上げられます．塩素は普通水素結合を生じない元素となっています．塩素よりも電気陰性度の小さい窒素が水素結合をするというのは原子が小さいということも要件の一つだということです．塩素の反応性は電気陰性度では説明できないようですのでラディカル生成能力で考えました．水溶液中ではイオン反応が多いと思いますが気相ではラディカル反応が主だろうと思います．

yama さんのレス (2007/08/26(Sun) 22:35)

振動の自由度については，運動エネルギーだけでなく，（調和振動の場合は）ポテンシャルエネルギーにもRT/2のエネルギーが分配されるので，振動を考えたときの２原子分子気体の定積モル比熱は7R/2，従って定圧比熱は9R/2になると思います．固体の比熱がほぼ3Rになるのもポテンシャルエネルギーの寄与があるからです． 従って定圧比熱が4R程度ならば，振動の自由度が十分励起されているとは言えないでしょう．

反応性については，komagatakeさんのおっしゃる通り，いろいろな要素を考えないといけないので，電気陰性度の寄与が最も大きいとは言えないかもしれませんね．

yama さんのレス (2007/08/26(Sun) 23:40)

水素分子についても量子効果があらわれているように思われます． つまり，低温で剛体モデルの値より小さくなっているのは，回転の自由度が十分励起されていないためだと思います． 量子論では，運動量は連続な値をとりますが，角運動量は離散的な値をとるため，低温では回転の自由度が十分励起されないわけです． 従って十分低温では，回転の自由度にはほとんどエネルギーが分配されないので，比熱は単原子分子の値に近づく・・・と言いたいところですが，実際にはその前に液体になってしまうでしょうね．

ｋｏｍａｇａｔａｋｅ さんのレス (2007/08/27(Mon) 06:25)

ｙａｍａさん

振動の自由度が励起されているとＲＴエネルギーが増えて比熱が定積比熱が９Ｒ／２となるということです．振動だけ考えるとそうなるようにも思います．これだと値は納得できます．

エネルギーの配分先の自由度で７×（Ｒ／２）になりますね． 私はふと自由度６が最高と思ってしまいました． 金属の格子比熱で１方向にＲＴというのと同じですね． 間違っていました．