撃力 δ関数
撃力 δ関数
けん(大学2年) さんの書込 (2007/08/22(Wed) 17:56)
撃力,δ関数の問題です.
md^2x/dt^2=-kx+p0δ(t-t0) を考える.(m,k,p0,t0は定数,δはδ関数) これは単振動の系に時刻t=t0で撃力が作用する状況を表す.t<t0でx=0,dx/dt=0の条件の下で,x(t)を求めよ.
運動方程式の両辺にdx/dtをかけて,tで積分する(t0-εからt(>t0)まで,ε>0)と,t<t0でx=0,dx/dt=0の条件と,δ関数の性質から, (m/2)(dx/dt)^2=-(k/2)x^2+p0(dx/dt)(t0) となります. ここで,t→t0とすると, (m/2)(dx/dt)(t0)^2=p0(dx/dt)(t0)となり, (m/2)(dx/dt)(t0)=p0となります. しかし,p0の正しい値は,m(dx/dt)(t0)です. 上の式変形では,どこかでδ関数に関してまずい変形をしているのでしょうか. よろしくお願いします.
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/22(Wed) 21:35)
条件を考えると  からでなく
からでなく 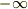 から積分すればいいでしょう.
から積分すればいいでしょう.
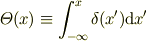
としたとき,
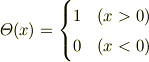
ですので,
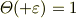
ですが,
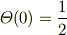
に注意してください.(8/25 訂正)
# このときの  は十分小さいが
は十分小さいが 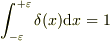 を満たしているとします.
を満たしているとします.
# 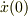 と
と 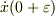 は区別をすべきです.
は区別をすべきです.
Re: 撃力 δ関数
MXK さんのレス (2007/08/24(Fri) 10:49)
δ関数の項が効いている間は,右辺第1項(復元力)は無視するというやりかたが簡単だと思います.直接積分ができるようになります. 因子1/2の原因は toorisugari no Hiro さんの指摘どおりで,速度が階段状の特異性をもつからです.
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/08/24(Fri) 18:24)
toorisugari no Hiroさん,MXKさん,解説ありがとうございます. limΘ(x)=1/2 はどうしてですか?また,δ関数に関数dx/dtがかけられている場合も,t→t0で1/2が出てくるのですか?
Re: 撃力 δ関数
MXK さんのレス (2007/08/25(Sat) 00:22)
δ関数の代わりに幅 T, 高さ f0 = p0 / T の矩形パルスを考えてみたらどうでしょう.復元力を無視すれば, dx/dt, x が求まるので,それから T→0 の極限を考えれば,いろいろ分かると思います.
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/25(Sat) 19:23)
別解です.
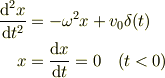
で考えましょう. 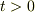 では単振動方程式なので,
では単振動方程式なので,
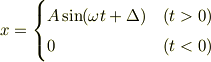
解が有界と仮定すると,すなわち,
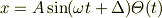
とおけます( 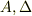 は定数,
は定数, 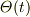 は階段関数).これより,
は階段関数).これより,
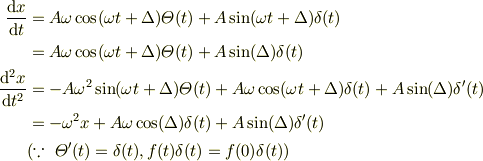
方程式と比較すると
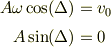
だから
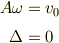
を解に代入すると
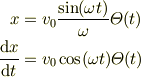
がえられます. なお,この結果より
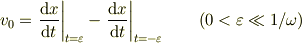
となります.
# MXKさんの助言に従い訂正しました.
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/08/26(Sun) 18:56)
>MKXさん limΘ(x)=1/2が分かりました.ありがとうございます.
>toorisugari no Hiroさん 解をAsin(ωt+Δ)Θ(t) とおけるのはどうしてですか?t<0,0<tのときは分かるんですが,t=0のときが分かりません.
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/27(Mon) 13:02)
> 解をAsin(ωt+Δ)Θ(t) > とおけるのはどうしてですか?t<0,0<tのときは分かるんですが,t=0のときが分かりません.
有界と仮定しているからです. 別に,
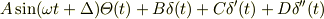
として計算してもかまいません.
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/08/27(Mon) 20:58)
t=0でどうしてサイン関数と階段関数の積になるのか,ということです. t<0.0<tは分かるんですが.
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/28(Tue) 12:00)
> t=0でどうしてサイン関数と階段関数の積になるのか,ということです. > t<0.0<tは分かるんですが.
質問の意味がつかめません.
 で
で 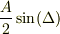 という値でなく,他の有限な値をとってもいいのでは?ということなら理解できます.そういう質問だと解釈して進めます.(
という値でなく,他の有限な値をとってもいいのでは?ということなら理解できます.そういう質問だと解釈して進めます.(  で発散する場合についてはすでに述べました.)
で発散する場合についてはすでに述べました.)
たとえ微分方程式にδ関数が現れても,解に任意の不連続性や特異性が現れるわけではありません.
非同次微分方程式の考え方を思い出してもらえばいいのですが,特解は非同次項及びその微分や積分の線形な組み合わせで表現されます.非同次項がδ関数の場合,解に現れる特異性は階段関数やδ関数およびδ関数の微分の線形和で表現されるはずです.
それで表現できない不連続性は最初から除外されます.
 で
で 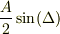 以外の有限な値
以外の有限な値 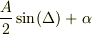 をとるとしたら
をとるとしたら 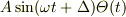 に
に 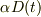 となる付加項をつけることになります.ただし,
となる付加項をつけることになります.ただし,
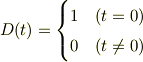
です.しかし,この 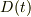 は階段関数やδ関数等の線形和で表現できないので除外されます.結局,δ関数以外の付加項はあり得ません.
# そもそも上の
は階段関数やδ関数等の線形和で表現できないので除外されます.結局,δ関数以外の付加項はあり得ません.
# そもそも上の 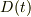 は除去可能特異性なので,最初から無視できます.
は除去可能特異性なので,最初から無視できます.
ある意味での連続性が微分方程式にδ関数を含む場合でも満たされなければいけないということですね.ここら辺はMXKさんのおっしゃった,δ関数の有界な近似関数で考えてみればよいと思います.
Re: 撃力 δ関数
MXK さんのレス (2007/08/29(Wed) 11:36)
デルタ関数や階段関数はある種の理想的な極限なので,やはり近似的な関数で考えることが必要だと思います.
それから,No. 17619 の冒頭の式の 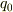 は
は 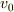 と書いたほうが次元的に分かりやすいと思います.元の問題でも,
と書いたほうが次元的に分かりやすいと思います.元の問題でも, 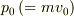 のように運動量を示唆する記号が選ばれています.
のように運動量を示唆する記号が選ばれています.
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/08/29(Wed) 18:43)
>toorisugari no Hiroさん ご丁寧な解説ありがとうございます. >有限な他の値をとってもいいのでは?ということなら理解できます. その通りです.質問の意味が曖昧だったようで申し訳ありません.
書いて頂いた別解の式で, dx/dt=v0cosωt・Θ(t) がありますが,この式にt=0を代入すると, dx/dt(t=0)=v0/2 となります.お書きになったv0はどうやって導出したのでしょうか?
>MXKさん 近似的な関数で考えることは,δ関数を考えるときの参考になりました.ありがとうございます.
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/29(Wed) 18:59)
えっと今ちょうどNo.17653を改訂したところなので,それも見てください.
> 書いて頂いた別解の式で, > dx/dt=v0cosωt・Θ(t) > がありますが,この式にt=0を代入すると, > dx/dt(t=0)=v0/2 > となります.お書きになったv0はどうやって導出したのでしょうか?
何を導出するのを聞かれているのかわかりませんが,,,, 重要なのは速度そのものでなく速度の変化量のはずです.ですから,
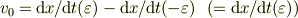
と書きました.
# 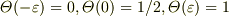 は理解されているのですよね?
#
は理解されているのですよね?
#  は
は 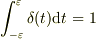 ,
, 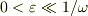 を満たします.
を満たします.
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/08/29(Wed) 19:29)
># は理解されているのですよね?
それは理解しています.
v0=dx/dt(ε)-dx/dt(-ε) をどうやって導出したんでしょうか?
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/29(Wed) 19:41)
> ># は理解されているのですよね? > それは理解しています. > v0=dx/dt(ε)-dx/dt(-ε) > をどうやって導出したんでしょうか?
どこがわからない,疑問なのか,詳しく説明してもらえませんか?
Re: 撃力 δ関数
MXK さんのレス (2007/08/29(Wed) 20:06)
わたしも疑問点が掴めていませんが...
最初のころの, 力 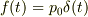 に速度
に速度 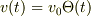 をかけて
積分するところですが,
をかけて
積分するところですが,
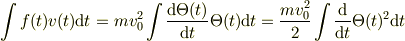
というのは大丈夫でしょうか?
 での値が1/2というのが問題ではなく,
前後での差が大事だというのは, すでに指摘されている通りです.
での値が1/2というのが問題ではなく,
前後での差が大事だというのは, すでに指摘されている通りです.
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/29(Wed) 20:57)
> 大丈夫でしょうか?
どちらに質問されているのでしょうか?(笑)
私だとして,やりますね.
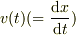 が
が  で有界だが,不連続
で有界だが,不連続  を持つなら,
を持つなら,  近傍で
近傍で
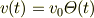
と書ける.これを
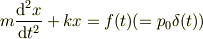
の ![[-\varepsilon,\varepsilon]](http://hooktail.maxwell.jp/bbslog/ab4d52f4842cc8b216deac5cc4c05a8d.png) におけるエネルギー積分に代入すると(
におけるエネルギー積分に代入すると(  については既述),
については既述),
![\frac{1}{2}m v_0^2 - 0 &= \int_{-\varepsilon}^\varepsilon f(t)v(t){\rm d}t\\&= v_0p_0 \int_{-\varepsilon}^\varepsilon \frac{{\rm d} \varTheta(t)}{{\rm d} t}\varTheta(t) {\rm d} t\\&= \frac{v_0p_0}{2} \int_{-\varepsilon}^\varepsilon \frac{{\rm d}}{{\rm d} t}\varTheta(t)^2{\rm d} t\\&= \frac{v_0p_0}{2} [\varTheta(t)^2]_{-\varepsilon}^\varepsilon \\&= \frac{v_0p_0}{2}\\\therefore p_0 &= mv_0](http://hooktail.maxwell.jp/bbslog/cd6a0ee510c8348dc3e941b2b1cd3922.png)
(  は連続だからエネルギーの計算からはずしています.)
なお,
は連続だからエネルギーの計算からはずしています.)
なお,
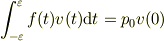
としても 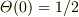 ですから結果はおなじですね.
ですから結果はおなじですね.
Θ(0)=1/2 ?
toorisugari no Hiro さんのレス (2007/08/29(Wed) 23:35)
MXKさん だんだん,わからなくなってきました.
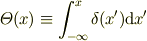
となる 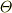 に対して,
に対して, 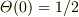 って正しいんでしょうか?
って正しいんでしょうか?
δ関数が偶関数であることを認めるなら,
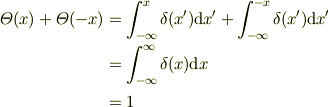
となるので, 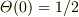 ですよね.
ですよね.
でも, 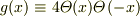 という関数を考えると,
という関数を考えると,
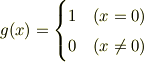
という,前の記事で除外した関数になってしまいます. しかも,
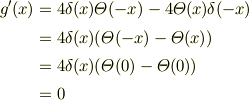
ですから 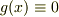 ですね.
ですね.
たぶん,教科書通り,「超関数の積は御法度」ということで片が付くとは思うのですが,そうなると 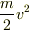 や
や 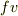 を考えることすらそもそもできません.
を考えることすらそもそもできません.
間をとって「 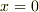 で特異点を持つ超関数の積の
で特異点を持つ超関数の積の 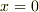 における値は御法度」とするべきでしょうか?(ex.
における値は御法度」とするべきでしょうか?(ex. 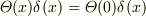 は御法度)
は御法度)
それならば,前の記事No.17668の前半の計算は良いけれど,後半の 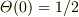 あるいは
あるいは 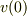 を使う計算は,偶然正しい結果だけど無意味ということになりますね.
を使う計算は,偶然正しい結果だけど無意味ということになりますね.
Re: Θ(0)=1/2 ?
MXK さんのレス (2007/08/30(Thu) 01:18)
教科書的には「超関数の積は定義できない」,「デルタ関数は原点で連続な関数のみを対象としている」
なので困った状況ですが,粗視化を用いる立場からは結構大丈夫だと思っています.
粗視化した場合の力 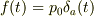 と速度
と速度 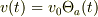 が
が
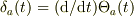 で関係づけられているからです.
因子 1/2 が出るのはこの性質によるもので,
で関係づけられているからです.
因子 1/2 が出るのはこの性質によるもので, 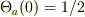 を要請する必要はありませんし,
成り立っている保証もありません.
微分積分の関係にない,デルタ関数に収束する関数と,階段関数に収束する関数の積を積分しても,
意味のある結果は出てきません.そういう意味で教科書は正しいといえます.でも物理における
典型的な状況を扱えない枠組はいまいちだと思います.
を要請する必要はありませんし,
成り立っている保証もありません.
微分積分の関係にない,デルタ関数に収束する関数と,階段関数に収束する関数の積を積分しても,
意味のある結果は出てきません.そういう意味で教科書は正しいといえます.でも物理における
典型的な状況を扱えない枠組はいまいちだと思います.
撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/30(Thu) 02:44)
MXKさん,ありがとうございます.
元の問題に戻ります.
エネルギー積分をつかった導出には 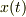 の
の  における連続性(あるいは
における連続性(あるいは 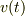 の有界性)を使っています.でも,そもそも
の有界性)を使っています.でも,そもそも 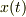 の
の  における有界性(あるいは連続性)がわかっていれば,
における有界性(あるいは連続性)がわかっていれば, 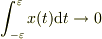 ですから,方程式をそのまま積分して
ですから,方程式をそのまま積分して
![\left[m\frac{\mathrm{d}x}{\mathrm{d}t}\right]_{-\varepsilon}^{\varepsilon}=p_0](http://hooktail.maxwell.jp/bbslog/fa1ddc886e52a3b9913fd20a24b01200.png)
が得られます.
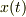 の有界性,あるいは,
の有界性,あるいは, 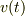 の有界性,を簡単に導く方法はないですかね?
の有界性,を簡単に導く方法はないですかね?
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/08/30(Thu) 13:09)
> x(t)の有界性,あるいは,v(t)の有界性,を簡単に導く方法はないですかね?
x(t)の有界性を直接先に出すという方法はないのかなと思います.
近いとしたら以下の論理でしょうか. 「 特異性とは何回か微分すると発散が現れる性質である.微分可能な回数が小さい程特異性は強い.
超関数は特異性を持つ.特異性の定義により,超関数を微分したものは,もとの超関数より特異性が強い.すなわち,絶対値関数より階段関数が,階段関数よりδ関数が,δ関数よりδ’関数が特異性が強い.
方程式
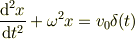
の解 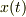 は特異性を持つが,
は特異性を持つが, 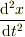 の方が特異性が強いので,左辺の特異性は
の方が特異性が強いので,左辺の特異性は 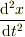 が担う.
が担う.
よって特異性の釣り合いから,特異点近傍では
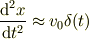
と近似(弱い特異性は無視)できる.
これを積分することで 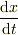 は階段関数型の特異性
は階段関数型の特異性 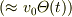 ,よって,
,よって,  は折れ線型(絶対値関数型)の特異性
は折れ線型(絶対値関数型)の特異性 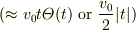 を主に持つことがわかる.つまり,
を主に持つことがわかる.つまり,  は連続である.
」
は連続である.
」
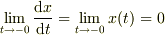 ですから,
ですから, 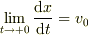 ,
, 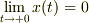 が得られるので,これを初期条件に
が得られるので,これを初期条件に 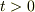 で通常の調和振動子の方程式を解けばいいですね.
で通常の調和振動子の方程式を解けばいいですね.
# ただ,文頭の特異性の強弱の箇所が怪しいですが....
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/09/13(Thu) 13:06)
出かけていました.遅くなってすみません.
v0=dx/dt(ε)-dx/dt(-ε) をどうやって導出したんでしょうか? というのは, dx/dt=v0cos(ωt)Θ(t) という結果から,どのようにして上式を導いたのかが分からないから教えてほしいということです.
それから,No.17668のtoorisugarinohiroさんのご説明の中で, dx/dtが…不連続0→v0を持つなら, とありますが,v0は与えられた運動方程式の右辺にある単なる定数なのに,どうしてそれがdx/dtのt=0の直後の値だと分かるのですか?むしろ,今はそうなることを導きたいです. よろしくおねがいします.
Re: 撃力 δ関数
スパイク さんのレス (2007/09/13(Thu) 13:51)
こんにちは.
横レス失礼致します.基本的なことなのですが, まず初めに,次元はご確認されましたでしょうか? #撃力は[N]近似しないと・・・
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/09/13(Thu) 17:02)
> v0=dx/dt(ε)-dx/dt(-ε) > をどうやって導出したんでしょうか? > というのは, > dx/dt=v0cos(ωt)Θ(t) > という結果から,どのようにして上式を導いたのかが分からないから > 教えてほしいということです.
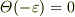 ,
, 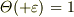 ただし,
ただし, 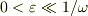 ,
をつかって,
,
をつかって, 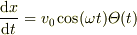 に対して
に対して
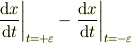
- を計算してみてください.途中まででもいいですから.
> それから,No.17668のtoorisugarinohiroさんのご説明の中で, > dx/dtが…不連続0→v0を持つなら, > とありますが,v0は与えられた運動方程式の右辺にある単なる定数なのに, > どうしてそれがdx/dtのt=0の直後の値だと分かるのですか?
「dx/dtのt=0の直後の値」ではなく「dx/dtのt=0の直前の値と直後の値の差」がv0です.
これについてはNo.17681で説明しているので,その記事でfollowできないところを質問してください.
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/10/01(Mon) 15:55)
遅れてすみません.
>スパイクさん どの式の次元のことでしょうか?
>toorisugari no Hiroさん
前回の1つ目の質問ですが, 第一項はv0cos(ωε) 第二項は0となりました. ε→0とすればv0になるということでしょうか. もしくは,ωε<<1から近似としてv0なのでしょうか.
2つ目の質問についてですが,No.17681の解は厳密な解ではなく,近似的な解と理解していいですか?
Re: 撃力 δ関数
toorisugari no Hiro さんのレス (2007/10/01(Mon) 16:28)
> もしくは,ωε<<1から近似としてv0なのでしょうか.
計算手順としてはそうです.ただし,近似として成り立つという意味ではなく 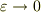 を採った「厳密な」ものと考えるべきです.
を採った「厳密な」ものと考えるべきです.
> No.17681の解は厳密な解ではなく,近似的な解と理解していいですか?
「近似」にはいろいろの解釈があります.ここではより弱い特異性を持つ解や,特異性を持たない解を無視するという近似です.(正確には近似と言うより特異性の評価ですね.)
例えば 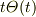 に
に 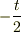 を加えたものは
を加えたものは 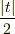 ですから
ですから
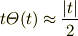
とできます. 同様に
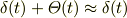
ですね.
特異性の評価で,方程式を簡単
( 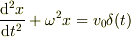
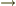
 )
にしましたが,得られた解は近似的なものではなく,特異性の強い部分に関しては厳密です.特異性を持たない部分に付いては,先の記事の後半に述べているように,特異性から得られた振る舞いを境界条件にして解けば得られます.
)
にしましたが,得られた解は近似的なものではなく,特異性の強い部分に関しては厳密です.特異性を持たない部分に付いては,先の記事の後半に述べているように,特異性から得られた振る舞いを境界条件にして解けば得られます.
Re: 撃力 δ関数
スパイク さんのレス (2007/10/01(Mon) 19:24)
>>スパイクさん >どの式の次元のことでしょうか?
元の方程式のδ関数の項の次元ですが. #確認されていたかな?と思っただけです.
Re: 撃力 δ関数
けん(大学2年) さんのレス (2007/10/02(Tue) 12:01)
>toorisugari no Hiroさん 特異性の評価のために方程式を簡単にするというのは見るのが初めてで戸惑ってしまいましたが,おかげさまで理解できました.ありがとうございました.
>スパイクさん ここではδ関数の次元はs^-1ですね.
Re: 撃力 δ関数
スパイク さんのレス (2007/10/02(Tue) 16:25)
>けんさん
>ここではδ関数の次元はs^-1ですね.
そうなんです.変数が増えた場合でも同様の手法で, 評価が出来るということだったんです♪
#理解されたようで,おめでとう御座います(^^♪