stream さんの書込 (2007/08/20(Mon) 07:51)

院試勉強中のstreamと申します．数日前に質問したばかりなのですが，また疑問が生じたので書かせていただきます．ご教授いただけると幸いです．

円柱座標を用いて次式で表される曲面がある． z=a*(1-(r/R)^2) r<R ただしa>0 z=0 r>R,r=R ただしz軸は鉛直上向きが正で，rはｚ軸からの距離である． この曲面上を一個の粒子が運動している．ただし粒子の質量はｍで，粒子は曲面の凸凹にかかわらず，常に曲面に拘束されたまま完全に滑らかに運動できるようになっている． 最初，粒子はx軸正方向の無限遠方から，x軸と平行で距離bにある直線軌道 y=b , 0<b<R に沿って等速度vで曲面の凸部分に進入したとする． 拘束力以外で粒子にかかる力は，重力だけであるとする．

長くなりましたが，上の問題文が最初に与えられている問題です．この拘束力というものがどちら向きのどんな力かがよく分からないのです． 設問には，粒子の全エネルギーとz軸回りの角運動量が保存することを示せ，とあるので，両者は保存するようなのです． 最初は曲面からの垂直抗力が働くと考えて，ラグランジアンを書いてr方向の運動方程式を書いて見ましたが，垂直抗力と遠心力の項が外向きなので，rが増えてしまい，曲面から離れてしまうと思います．

曲面上を滑らかに運動するときの条件がいまいち分かっていないのかもしれません．粒子が存在する点における，曲面の法線方向の力が釣りあう？という条件なのでしょうか？

長くなりましたが，よろしくお願いします．

ミュフ猫 さんのレス (2007/08/20(Mon) 09:18)

streamさん，こんにちは．

>粒子が存在する点における，曲面の法線方向の力が釣りあう？ >という条件なのでしょうか？

初速度vがある値より大きくなると，遠心力の法線方向成分の大きさが 重力のそれを越えてしまい，垂直抗力だけでは拘束しきれなくなるので， その場合は，垂直吸着引力（つまり，負の垂直抗力）も働くという条件では？ 自信ないけど．ｗ

ｙama さんのレス (2007/08/20(Mon) 10:43)

粒子が静止していない場合は，曲面の法線方向の力は一般には釣りあわないと思います． それはともかくとして，この問題の場合は拘束力を求めなくてもz軸まわりの角運動量やエネルギーの保存を示せるのではないでしょうか．

ところで，ラグランジアンはどんな式になりましたか？

zoro さんのレス (2007/08/20(Mon) 18:00)

横から失礼します．

とても難しい問題ですね．素人的に考えると，粒子が曲面に衝突した瞬間をどう処理するか想像出来ません．一種の反発係数みたいな設定が無いまま解けのでしょうか？

始めて拝見したタイプの問題なので気になりました...．宜しければ，本論の後にでも，回答下されば幸いです．

yama さんのレス (2007/08/20(Mon) 20:28)

「粒子は曲面の凸凹にかかわらず，常に曲面に拘束されたまま完全に滑らかに運動できるようになっている．」ということなので，曲面に沿って向きを変えるだけで速さは変化しないのではないでしょうか．

zoro さんのレス (2007/08/20(Mon) 22:47)

さらに失礼します．

＞曲面に沿って向きを変えるだけで速さは変化しないのではないでしょうか．

凹形の曲面に衝突するなら，またイメージ出来るのですが．凸型の曲面に衝突するとイメージ出来ないです(泣)．

それにしても，難しい問題ですね．当分，論議を拝見します．どうもお邪魔しました．

スパイク さんのレス (2007/08/21(Tue) 00:28)

streamさん，こんばんは．

本問は，解析的に解けます．

＃工学的な応用については，日常ご利用にになっておられるかと．

stream さんのレス (2007/08/21(Tue) 08:03)

みなさま，レスありがとうございます． ミュフ猫さん，やはり垂直抗力だけを考えると無理そうですよね．私もそう考えて，逆方向の力を考えたのですが，向きが法線方向向きなのだろうか？と疑問に思いまして．問題には拘束力が働く，とだけ書いてあり(拘束力以外の力は重力だけである，ということから)その拘束力が曲面から働くものなのか，はたまた粒子なので拘束力として静電気力でも受けているのか，と色々考えてしまいました．

それで混乱してしまったんですが，曲面上を滑らかに運動する条件は法線方向の力が釣りあう，で合ってますでしょうか？それで大丈夫なら，法線方向のみの拘束力と考えて今度もう一度やってみます．

yamaさん，拘束力が法線方向ならば，その力は粒子の速度成分と垂直で仕事をせず，またz軸周りの力のモーメントが0となり，全エネルギー，z軸周りの角運動量が保存することが示せるのですが．今考えると法線方向に働かないなら全エネルギーは一定ではなくなりますね． ラグランジアンは円柱座標で考えて L=1/2m((r')^2+(r*θ')^2+(z')^2)-mgz となると思います．'は時間微分です．

zoroさん，確かにその瞬間は難しいですね．吸着する感じでしょうか？

スパイクさん，やはり解析的に解けるのですね．

スパイク さんのレス (2007/08/21(Tue) 10:10)

みなさん，こんにちは．

streamさんへ

>スパイクさん，やはり解析的に解けるのですね．

ええ，大丈夫です（曲面に拘束されているため，保存則が成立することが分かります）．

ｙama さんのレス (2007/08/21(Tue) 11:31)

粒子は曲面上では自由に運動できるので，曲面の接平面方向には拘束力ははたらきません． 拘束力は，粒子が曲面から離れないようにはたらくだけなので，当然法線方向だけにはたらくことになります．（拘束力の向きは法線の正負どちらの向きも可能です．） 従って拘束力は仕事をしないことになり，重力が保存力であることを考えると，結局エネルギーが保存することになります． なお，前に書いたように，法線方向の力は一般には釣り合いません．

ところで，streamさんのラグランジアンですが，そのラグランジアンから無条件にラグランジュ方程式をつくっても正しい運動方程式にはなりません．というのは，そのラグランジアンでは粒子が曲面上に拘束されていることが考慮されていないからです． 運動は作用積分 ∫Ldt が極値をとるように行われますが，無条件で極値をとるわけではなく，拘束条件を満たすように極値をとります． 従って，拘束条件のついた条件付極値問題として考える必要があります．

条件付極値問題を解く一般的方法としては，ラグランジュの未定乗数の方法がありますが，今回の問題の場合は，拘束条件を用いて変数を減らすほうが簡単です．

すなわち曲面の式 z=a*(1-(r/R)^2) r<R ただしa>0 z=0 r>R,r=R を用いて，ラグランジアンからzとz'を消去します．当然 r<R の場合と，それ以外の場合でラグランジアンを表す式の形は違ってきますが，いずれにしてもラグランジアンはrとθおよびそれらの時間微分だけで表されることになります．つまり自由度に等しい数の座標を用いてラグランジアンが表されるわけです． このラグランジアンからrとθについての運動方程式を導くことができます． また，ラグランジアンが時間tを陽に含まないことからエネルギーの保存が導かれ，θが循環座標になることからz軸まわりの角運動量の保存が導かれます．

このように，ラグランジュ方程式を利用すれば，拘束力を直接扱うことなく運動を調べることができます．

ｙama さんのレス (2007/08/21(Tue) 13:08)

補足しておきます．

曲面を平面部分と凸部分に分けると，それぞれの部分を運動している間は，エネルギーもz軸まわりの角運動量も一定に保たれることが分かりますが，これらの境界を通過するときにどうなるかが問題です． 境界を通過するとき速さが変わらないとすれば，エネルギーが変化しないことは明らかです．しかし，このとき運動方向が変わるため，z軸まわりの角運動量は変化するのではないか・・・と思いましたがよく考えてみると変化はしないようです．（考えてみてください．）

zoro さんのレス (2007/08/21(Tue) 15:53)

素人の疑問を初等的力学の目で，すこし整理してみます．

与えられた曲面の方程式は；

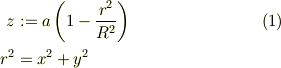
この曲面を陰関数にして，

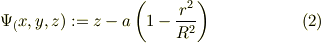
と表現すれば，この面の法線ヴェクタは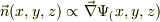， で与えられます．これをゴリゴリ計算すると；

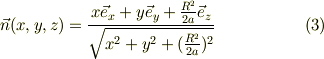
となるようです．位置ベクトルのxy平面での射影成分に比例し，z方向には一定値となるようなヴェクタのようです，面白いですね．

ある曲面上に粒子が乗ったとすれば，少なくとも曲面から粒子への抗力は，

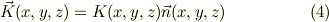
しかないでしょう． おそらくyamaさんがお書きになっているように，この成分は，運動方程式を円筒座標にする事と，重力が粒子を曲面に押し付けて，粒子が曲面にトラップされている．したがって，接平面成分の運動の解から，逆に 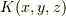が与えられるのだろうと思います．

＃糸で吊り下げられた振り子を回転座標で解く時に，張力が方程式からみえなくなりますが，それと類似だろうと推測しています． ＃後は，解析力学を駆使しようが，円筒座標系の運動方程式をゴリゴリしようが，同じ結論がでると思います．

他方，水平飛行して衝突する粒子の速度は，題意により；

ですから，b=Rという極限で無い限り，式(3)，式(5)の内積はゼロになりません．

この速度成分が完全非弾性衝突すしない限り粒子は曲面にトラップできないと思います．

勿論，トラップされたら曲面にトラップした運動があるとは思いますが，どんな解； ・振動解， ・連続回転解， ・どっかで離れる などがあるのか楽しみです．streamさんの豪腕ぶりに期待しています．

勝手な事を書きましたが，どこかに落とし穴があるようにも思います．

stream さんのレス (2007/08/22(Wed) 07:27)

yamaさん，zoroさん，詳しい説明どうもありがとうございます． 設問には続きがあり，拘束力の感じが掴めなかったのでさっぱりでしたが，おかげさまで徐々に掴めて来た感じがします． お二人の考え方をもとに今日にでもみっちり考えてみたいと思います．