電磁気の問題に関して
電磁気の問題に関して
鉛筆の芯 さんの書込 (2007/08/14(Tue) 00:08)
夏休みの宿題で行き詰ってしまったので,教えていただけると幸いです.
問)面積が十分に大きい2枚の金属板A,Bが平行に置かれている.Bは接地されており,その電位は0である.また,AB間は真空であり,重力の影響は無視できる. Aの電位がVであるとき,以下の問に答えよ. (1)AB間の電場の強さと向きを求めよ. (2)BからAに向かって距離zの点における電位を求めよ.
(1)は一様な電界を求める式 E=V/d を用いて解くのだと思ったのですが,問題には極板間距離が与えられていません.極板間距離や極版の面積を用いないで電場を求めることができるのでしょうか? (2)も E=V/d の式を用いて解くのでしょうか?
Re: 電磁気の問題に関して
zoro さんのレス (2007/08/14(Tue) 02:01)
鉛筆の芯さん,初めまして.
この問題は,入試と言った正式な試験ではなくて,講義の中の宿題で,インフォーマルなものではないでしょうか?
気になるのは「重力の影響...」という記述がある所ですね.推定では,もっと長い問題の一部では在りませんか?
そうでないとすれば,
- 必要なパラメータは自分で設定して良いと思います.
- もしも,大学生さんなら,
 の線積分を考えて見てください.そうでないなら,教えて下さい.
の線積分を考えて見てください.そうでないなら,教えて下さい.
Re: 電磁気の問題に関して
鉛筆の芯 さんのレス (2007/08/14(Tue) 09:35)
すばやいお答えありがとうございます.
私は某高専の学生です.問に「重力の影響…」とあるのは,実は(3)が存在するからです.(3)は自力で解くことができたので,ここでは問いを省略させていただきました.
Re: 電磁気の問題に関して
zoro さんのレス (2007/08/14(Tue) 10:23)
>私は某高専の学生です.問に「重力の影響…」とあるのは,実は(3)が存在するからです.
なるほど,了解出来ました.(1)は,推察されているように出すのだろうとおもいます.
(2)については,下図を参考に考えて下さい. <pre> ポテンシャル:Ψ(x) ↑ | | V ・------------------------・V=Ψ(d) | | | | | | | | | | | ?どんな関数になるのだろうか? | | | | | | | | | | | | 0=Ψ(0) ・ーーーー・ーーーーーーー・ーーー→x軸 x=0 x=z x=d B点 A点 </pre>
両電極の間は真空であり,電荷の分布が無いのだから,
・電場強度, 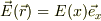 ,は一定;
,は一定; 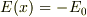 .
・
.
・ 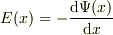 .
.
これを元に考えて見てくださいませんか.
Re: 電磁気の問題に関して
鉛筆の芯 さんのレス (2007/08/14(Tue) 10:55)
電界強度が一定より,ポテンシャルψの関数はパラメータxに比例するから,求める電位はψの関数をx=zからx=dまで積分すればいいのでしょうか?
Re: 電磁気の問題に関して
zoro さんのレス (2007/08/14(Tue) 13:29)
>求める電位はψの関数をx=zからx=dまで積分すればいいのでしょうか?
鉛筆の芯さんの質問の前後に,当方の図を替えてしまいました.基本は;
電場電場について,電極間に電荷がないので
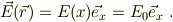
ポテンシャルの勾配が電場を与えますから;
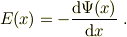
両式から,
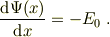
辺々を,x=(0..z)の区間について積分すれば,
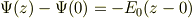
題意より, 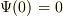 だから,...以下略.
だから,...以下略.