gradについて

gradについて

yy さんの書込 (2007/08/12(Sun) 21:13)

本サイトの ベクトル解析＞grad

の記事について質問です．

gradΦのイメージという見出しの記事なのですが， 図と「ベクトルgradΦはMにおける接平面に含まれる」 という二つの表現から，等位面Φの上にgradΦが寝そべっているイメージを受けます． しかしgradΦは等位面の法線方向をむいているので，等位面ΦにgradΦが垂直に突き刺さっているイメージではないでしょうか．

皆様の意見おきかせください．

Re: gradについて

zoro さんのレス (2007/08/13(Mon) 21:35)

yyさん，初めまして．

プロジェクトの方々は旅行などで不在かも知れませんね．

第三者の意見としては，仰られた図と説明は，途中経過でこれから修正するのでは無いでしょうか．

ポテンシャルが一定のときの感触を書いてみましょう．ある点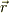， \vec r と，其の近傍点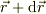， \vec r +\mathrm{d} \vec r が同一の等ポテンシャル面にあると仮定すれば，

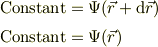
\text{Constant} &=\Psi(\vec r +\mathrm{d} \vec r) \\\text{Constant} &=\Psi(\vec r )

辺々を引くと，右辺は 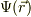\Psi(\vec r) の全微分であること，基底ベクトルの内積，ナブラ演算子の定義から，次のように表す事が出来る：

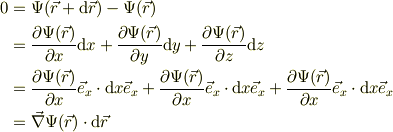
0 &= \Psi(\vec r +\mathrm{d} \vec r) -\Psi(\vec r)\\&= \frac{\partial \Psi(\vec r)}{\partial x}\mbox{d}x +\frac{\partial \Psi(\vec r)}{\partial y}\mbox{d}y +\frac{\partial \Psi(\vec r)}{\partial z}\mbox{d}z\\&= \frac{\partial \Psi(\vec r)}{\partial x}\vec e_x \cdot \mbox{d}x \vec e_x +\frac{\partial \Psi(\vec r)}{\partial x}\vec e_x \cdot \mbox{d}x \vec e_x +\frac{\partial \Psi(\vec r)}{\partial x}\vec e_x \cdot \mbox{d}x \vec e_x \\&= \vec \nabla \Psi(\vec r) \cdot \mbox{d}\vec r

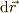今，仮定により， \mbox{d}\vec r は，等ポテンシャル面の中である．従って，此れと内積がゼロとなるので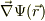， \vec \nabla \Psi(\vec r) は，等ポテンシャル面の法線ヴェクタとなる，と思います．

アスキー・アートでは，2Dしか描けませんが，トライしてみましょう；

<pre>

→ →

ygrad Ψ( r )⊥ dr ｜ ／ ｜／ ｜＊＊＝点M ｜／→ ｜→／ dr→ →→ ｜r ／ 等ポテンシャル面：Constant = Ψ( r ) = Ψ( r +dr ) ｜／ ｜／ ｜／ ｜／ ・ーーーーーーーーーx ／ 原点O ／

z

</pre>

点Mと 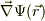\vec \nabla \Psi(\vec r) とを含む断面の拡大図を考えれば，等ポテンシャル面も近似的に並行．

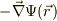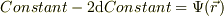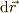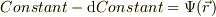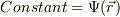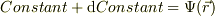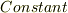<pre> -\vec \nabla \Psi(\vec r) ↑ ____-------------------│------------------______ --- │ --- Constant -2\mbox{d}Constant = \Psi(\vec r) ___---------------│---------------___ ------ │ \mbox{d}\vec r ------___ Constant - \mbox{d}Constant = \Psi(\vec r) _--------------＊──→--------__ __-- ----___ Constant = \Psi(\vec r) --- __---------------------------___ __-- --__ -- ----- Constant + \mbox{d}Constant = \Psi(\vec r) </pre>

この図を， Constant の等高線と見直せば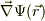， \vec \nabla \Psi(\vec r) は，ポテンシャル面を 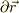\partial \vec r ずれたときの変化率と考えて；

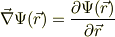
\vec \nabla \Psi(\vec r) = \frac{\partial \Psi(\vec r)}{\partial \vec r}

と書く場合もありますが，後から見ると解り難いので，乱用はしない方が良いと思います．少なくとも，最後には，逆書き換え；

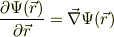
\frac{\partial \Psi(\vec r)}{\partial \vec r} =\vec \nabla \Psi(\vec r)

を入れて置かれる事をお勧めします．

Re: gradについて

zoro さんのレス (2007/08/15(Wed) 22:05)

yyさん，

ご指摘の「grad」のみを拝見して，先にお示しした「私の感触」を書いてみました．

今日は，昼間に予定が入っていたのがキャンセルになり，上記のページの関連記事を多少拝見しました．どうやら；

・ベクトル解析

というページの，「ベクトル解析１」という項目の；

# スカラー場と勾配

# 方向微分

などと関連しそうです．

私のように数学に疎い者には，少なくとも，上記の三つのページ；スカラー場と勾配，方向微分，grad；においては，絵と文章と式の間の整合性が低いように思います．「grad」だけを拝見したときは，お二人の筆者の方々が前半と後半を書かれて，論議がされないままになったように感じましたが，上記の２ページと比較してみると，そのような観点は間違えだったように感じています．

「grad」は力学や電磁気学の初歩を学んだ方が，ベクトル解析に入る時に，一番始めに出て来る「偏微分ベクトル型演算子」ですよね．なので，簡明な説明が期待されます．

是非ともこれらの著者さん一人でなく，プロジェクトの皆さんのご検討とご改訂をお願いしたいと思います．

もしも，私の意見に誤りや誤解が在れば，ご意見を戴きたいと思います．じっくりと，論議させて戴きたいと，おもいます．

Re: gradについて

yy さんのレス (2007/08/19(Sun) 00:31)

zoroさん，お返事ありがとうございます．

等ポテンシャル面内のベクトルとの内積がゼロになるということは，やはりgradΨは等ポテンシャル面の接平面に含まれるのではなく，等ポテンシャル面の法線ベクトルとなるのですね．

スカラー場と勾配，方向微分のページ見させていただきました． 私は特別に不自然に感じることなく読めたのですが，どこか改善すべき箇所があるのでしょうか．

ベクトル解析奮闘記1

の「自宅で復習（gradの巻）」にもわかりやすい解説がありました． これは二次元空間の話ですので，三次元目に関数fがとれるのでわかりやすいですね．この例で言えば，等ポテンシャル線（二次元なので面ではなく線，等高線）は直線 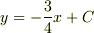y=-\frac{3}{4}x+C (Cはconstant)です．これはあくまで二次元の話ですので，gradｆは三次元ではなく，xy平面に投影した（図で言えば真上から見た）二次元ベクトル（３，４）です．

三次元で考えると・・・たとえば三次元空間に温度Tが分布している場合を例として考えます． ある点Aに立って見てみますと，その点Aの周り（ごく近傍）で一番温度が高い方にgradTが向くはずです．身体をgradTの方に向けると，前方が暖かいということは，相対的に背後が寒く，上下左右は立っている場所と同じ温度ということになります．この上下左右が等ポテンシャル面です． それらの様子を外から見てみると，空間に満たされたgradTの集まりは，熱源のほうを指しているはずです．（空間に満たされた熱伝達物質の熱伝導率の分布や，気流で空間内の流体が対流している場合は，熱源から遠方の点でgradTが熱源の方向を向いているとは限りません．） 熱源が点であれば等ポテンシャル面は同心球状に，熱源が線であれば円筒状に，熱源が面であればその面から層状に等ポテンシャル面が並ぶはずです．等ポテンシャル面からはgradTが熱源の方を向いて，正確に言えばより高いポテンシャルを持つ等ポテンシャル面の方を向いて生えています．

と，こんなイメージで理解しているのですが，なにか間違いがあれば是非ご教授ください．

Re: gradについて

Joh さんのレス (2007/08/19(Sun) 00:58)

yyさん＞

gradの記事を書いた者です．ご指摘ありがとうございます． 多忙のため掲示板も見ておらず，返信が遅れましてすみません． 該当記事は書き直そうと思いますが，改訂には少し時間が かかると思いますので，しばしご容赦ください． m(_ _)m

zoroさん＞

＞プロジェクトの方々は旅行などで不在かも知れませんね． 憶測で勝手なことを書くのはやめてくださいませんか．不愉快です．

また，プロジェクトへの要望・ご意見はいつでも歓迎ですが，掲示板ではなくプロジェクト宛のメイルでお願いします．その際，他の人にも理解しやすい日本語で，普通の言葉を使って要点だけ書くようにお願いします．また，必ずしもご希望に沿った対応ができるわけではないことをご理解ください．

Re: gradについて

zoro さんのレス (2007/08/19(Sun) 12:09)

yyさん，

＞等ポテンシャル面内のベクトルとの内積がゼロになるということは，やはりgradΨは等ポテンシャル面の接平面に含まれるのではなく，等ポテンシャル面の法線ベクトルとなるのですね．

この解釈で正しいと，私は考えます．

＞スカラー場と勾配，方向微分のページ見させていただきました． ＞私は特別に不自然に感じることなく読めたのですが，どこか改善すべき箇所があるのでしょうか．

私は，学生の頃「grad」は等ポテンシャル面からすんなりと理解出来たのですが，方向微分には，とても人工的な感触を受けて嫌いでした．それも在りますが，ここに引用した3つのページでは，話の流れが途切れ途切れで，理解しにくく，さらに「等ポテンシャル面の接平面に含まれる」かのように見える絵では，混乱の極まるように感じます．

＃昔の経験では，夏休み後にベクトル解析が始まるので，夏休みに自習される学生さんが多数いらっしゃり，このページを見る方も多かろうと推測しました．

＞ベクトル解析奮闘記1 ＞ http://www12.plala.or.jp/ksp/vectoranalysis/vecFuntou1/ ＞の「自宅で復習（gradの巻）」にもわかりやすい解説がありました． ＞これは二次元空間の話ですので，三次元目に関数fがとれるのでわかりやすいですね．

私は，頭が固いほうなので，逆に「二次元空間」だと考えにくいですね．あえて二次元空間で考えるなら，「等ポテンシャル線」や「ある点でのgradΨ」を書き込まないと誤解されるように感じます．

【追伸】13:03ころ

「ある点でのgradΨ」は図示してありますね．これに「等ポテンシャル線」を加えると，イメージが確りすると思います．

＞三次元で考えると・・・たとえば三次元空間に温度Tが分布している場合を例として考えます． ＞ある点 Aに立って見てみますと，その点Aの周り（ごく近傍）で一番温度が高い方にgradTが向くはずです．身体をgradTの方に向けると，前方が暖かいということは，相対的に背後が寒く，上下左右は立っている場所と同じ温度ということになります．この上下左右が等ポテンシャル面です．

なるほど，解り易い比喩ですね．お恥ずかしい事に今回の説明を再考している時に，「gradΨの向き」が「Ψの増加方向」にあるのを再認識しました．昔，方向微分の考え方に納得で来なかった自分が，いまごろ納得出来ました(笑)．

〜〜〜

Johさん，

＞＞プロジェクトの方々は旅行などで不在かも知れませんね． ＞憶測で勝手なことを書くのはやめてくださいませんか．不愉快です．

タイム・スタンプを良く見ていただきたいのですが，yyさんのご発言から丸一日，どなたのフォローが無いようだったので，そのように書きました．当然，断定形では書いてありませんね．また，この時点では「grad」の原著者の方を確認していませんでした．

むしろ，ご自分と異なる意見がでてきたら，どこがどう違ったかを，フェアに論じれば善いだけではないでしょうか？しばしば他のスレッドに於いても，私の書いた意見が「間違えている」というコメントをJohさんから戴きましたが，それぞれの掲示板のなかで論議してきた積もりです．

他人の意見に対して，論議以外で「不愉快」を引き起こす論議をするのは如何なものかと思います．私は，yyさんの疑問点を見るうちに，「grad」での説明は，初心者さんに誤解引き起こし易いだろうと感じたので意見を書いたまでのことです．論議が在れば，このスレッドでお願いしたいと思います．

Re: gradについて

zoro さんのレス (2007/08/19(Sun) 15:53)

yyさん，

学生の頃，友人達とポテンシャルとその勾配についの論議でかいた絵を思い出しましたので，ご参考までに書いてみます；

<pre>

ポテンシャルの大きさ ↑ ｜ ｜ ** ｜ * ｜ **** ｜ **** ｜ **** ｜ * ｜ * ｜ ** ｜ ** ｜ ** ｜ * ( →｜ *-gradΨ の橇(ソリ)で雪の斜面を落下

Ψ( r ) ・ *** ＿)

｜ ｜*** ｜ ｜ * ｜ ｜ * ｜ ｜*** ｜ ｜ * ｜ ｜ ** ｜ ｜ * ｜ ｜ ** ＋ーーーーーーーーーーーー・ーーーーーーー→ ０ →

r

</pre>

自分で，なにか解らなくなった時に，上の絵みたいなイメージを思い浮かべます；

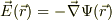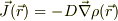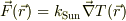（１）静電場では，球殻表面の正電荷や，正の電荷を持つ面がもつ，正のポテンシャルから電場， \vec E(\vec r)= -\vec\nabla \Psi(\vec r) に乗ってせん積分する様なイメージ． （２）角砂糖を真水にいれて，その中心の高い濃度から拡散流， \vec J(\vec r)= -D\vec\nabla \rho(\vec r) として出て行く． （３）yyさん流の，冷たいスキー場でのだるまストーブの温度勾配にヒトの顔が向く力， \vec F(\vec r)= k_{\mathrm{Sun}}\vec\nabla T(\vec r) とか．

Re: gradについて

G さんのレス (2007/09/06(Thu) 23:45)

Hom(Tp(M),R)とか双対に留意； ヒカル地面に竹が生え vector 場-Grad 場を含めた 紹介するのが「惜しい」「もったいない」ほど豊に図示されております；

Http://www.math.harvard.edu/~knill/teaching/math21a/

Re: gradについて

zoro さんのレス (2007/09/07(Fri) 00:35)

Gさん，拝見しました．

私のように，要領の悪い人間には，コンパクトだと逆に怖い気がしますが...．

一応，パラパラ読みをしました．図の使い方，レイアウトの見やすさには脱帽です．

高校から大学前期のなかで，大枠としてこんな感じの「直裁で，解り易い図，式」の解説が日本語で書かれていると良いですね．

ご教示，感謝します．