電子の識別

モヒ… さんの書込 (2007/08/09(Thu) 09:48)

「２つの電子は区別できない」と大発見のように書いてありました．確かに，色も形もないし，キズも印しもつけられないので正しいと思いますが，それがどうしたの？って感じです．「人間の限界」なのでしょうか？それとも不確定性のように「神もわからない」ことなのでしょうか？識別できないことによりなにか新しい発見とかあったのでしょうか？いまいち大発見のようには感じられないのですが…

Re: 電子の識別

zoro さんのレス (2007/08/09(Thu) 10:45)

モヒ…さん，はじめまして．

電子に自分のHNでも付けられると愉快そうですね．

さて2つだけの系を考えます．例えば，電子2個だけとか，光子2個だけとか．

古典力学や古典電磁気学では，一番目とか二番目とかのラベルを貼れた筈なのですが，量子力学ではラベルが貼れない，言い換えれば，「２つの電子は区別できない」と言えるのかもしれません．

＃以下に，すこし簡単な説明を試みます．あまりにも不正確だとお考えの識者の方がいらしたら，是非ともご解説をお願いします．

でも，量子力学では，波動関数というものを通して，量子系を表現します；２つの電子の波動関数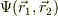＝ $\Psi(\vec r_1,\vec r_2)$

問題は，個々の電子が区別出来ないとして，座標を入れ替えたらどうなるのか，たとえば，

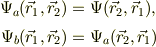
$\Psi_a(\vec r_1,\vec r_2) &= \Psi(\vec r_2,\vec r_1) ,\\\Psi_b(\vec r_1,\vec r_2) &= \Psi_a(\vec r_2,\vec r_1)$

幾ら量子力学といえども，二回位置を交換すれば，状態は元に戻る筈です．仮に一回の交換で，波動関数が係数倍替わるとすれば；

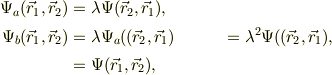
$\Psi_a(\vec r_1,\vec r_2) &= \lambda\Psi(\vec r_2,\vec r_1),\\\Psi_b(\vec r_1,\vec r_2) &= \lambda \Psi_a((\vec r_2,\vec r_1) &= \lambda^2 \Psi((\vec r_2,\vec r_1), \\&= \Psi(\vec r_1,\vec r_2),$

最後の2つの式が等しいから；

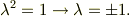
$\lambda^2=1 &\to \lambda = \pm 1.$

二粒子系の波動関数で，粒子の座標を交換すれば，二種類の交換性があり得て；

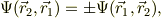
$\Psi(\vec r_2,\vec r_1) = \pm \Psi(\vec r_1,\vec r_2),$

となります．

電子や核子のような1/2スピンの粒子が「-」の交換性を示し，フェルミ-ディラック粒子，略してフェルミオンとかフェルミ粒子と呼ばれます．この場合，２つの粒子が同一の状態で接近する事が出来ません．試しに粒子2の座標を粒子1の座標にします， $\vec r_2 \to \vec r_1$ ；

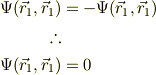
$\Psi(\vec r_1,\vec r_1) &= -\Psi(\vec r_1,\vec r_1)\\\therefore\\\Psi(\vec r_1,\vec r_1) &= 0$

という奇妙な結果になるからです．逆に2つの電子が，逆向きのスピンを持っていたら，同一の場所を占有する事が可能です．この結果，原子の同一軌道にはスピンが上下になった2つの電子が入る事が出来るのですね．

他方，「+」の例は，光子やα粒子のように，スピンが０の粒子です．この場合，２つの粒子が同一の状態で接近する事が出来ます．ですから，エネルギ準位の低い基底状態に，いくらでも重なり合う事ができます．この様な交換性に従う粒子を，ボーズ-アインシュタイン粒子，簡略して，ボーズ粒子なり，ボゾンと呼びます．

このように，同一粒子の振る舞いを，空間の対称性から性格付けを出来るのは愉快ですね．「CPT対称性反転」などで，調べると如何でしょうか？

Re: 電子の識別

モヒ… さんのレス (2007/08/10(Fri) 01:02)

ん〜と，言いますと具体的な現象はどんなことが起こるのでしょうか？

Re: 電子の識別

クロメルさんのレス (2007/08/10(Fri) 01:25)

区別できるできないといえば確率論でよく出てくる話ですよね．確率を扱う物理といえば統計力学です．というわけで，統計力学を見てみますと，エントロピーや分配関数が，粒子が区別できないということを考慮しないと，現実を記述できる関数として，求まりません．

またうろおぼえですが，量子力学で二粒子が衝突して非常に接近した方向に向かって散乱されるとき，同じ粒子が近い場所に散乱されるときは，違う粒子どうしが同近い場所に散乱される確率の二倍になります．これも粒子が区別できないことに由来します．これについては詳しく覚えていないので，もし興味がおありなら「ファインマン物理学?量子力学」岩波書店をご覧ください．

Re: 電子の識別

zoro さんのレス (2007/08/10(Fri) 09:15)

＞「２つの電子は区別できない」と大発見のように書いてありました．

この出典はどちらでしょうか？宜しければ，其の解説のなかで触れている，具体例で解りにくい所を書いて戴けば，こちらも考え易いですよ．

＞具体的な現象はどんなことが起こるのでしょうか？

私の場合，水素のエネルギ準位の量子力学的計算を知った後にも，なぜ同一準位に二個の電子しか入れないかという点が納得出来ませんでした．『電子がフェルミオンだとすれば，自然に「スピンが逆」の場合だけが許される』というのを知って，大変に感銘を受けました．

複雑な計算や，特殊な仮説の組み合わせから出たのでは無く，とても簡単な思考から，色々な分野に応用出来る指針を与えたのが，凄いと思います．

私は，物性物理には疎いのですが，フェルミオンやボゾンが別々な統計に従う事によることもその大きな成果だと感じます．ひいては，電子がフェルミオンである故に，半導体のバンド・ギャップが発生しているのでしょう．もし，電子がボゾンだったらギャップなど産まれる余地がありませんね．

素粒子や原子核の世界でしたら，先に書いた対称性は，大枠の指針として大切だろうと思います．

このような疑問は，勉強を進めながら，何度も自問自答して行くのも，良い勉強法の一つかも知れません．

[home] [掲示板] [ページの先頭]