反・共ベクトル

home > 掲示板 >

このページのPDF版

サイトマップ

反・共ベクトル

盾矛さんの書込 (2007/08/07(Tue) 09:31)

相対論を勉強中です．反変ベクトル，共変ベクトルの概念がイマイチわかりません．どういう性質のものを反変・共変というのかは参考書を見てわかりましたが，丸暗記でしかありません．

・なぜ反変・共変ベクトルという概念が生まれた(必要だった)のか・反変・共変ベクトルを使用することのメリットはなにかこの辺りを教えてくれませんか

Re: 反・共ベクトル

Dia さんのレス (2007/08/07(Tue) 12:10)

よく理解できていない私がレスするのは差し出がましいとは思いましたが，

http://www12.plala.or.jp/ksp/vectoranalysis/index.html

こちらの「共変ベクトルと反変ベクトル」と，それに続く項を読んでみるとよいのではないかと思います．

Re: 反・共ベクトル

toorisugari no Hiro さんのレス (2007/08/07(Tue) 14:54)

> ・なぜ反変・共変ベクトルという概念が生まれた(必要だった)のか > ・反変・共変ベクトルを使用することのメリットはなにか

のご質問にお答えしたいと思いますが長くなります．

以下，3次元ユークリッド空間を考えます．

ベクトルを成分表示する場合は，普通「正規直交基底」，すなわち，互いに直交する単位ベクトルの組 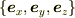$\{\bm{e}_x,\bm{e}_y,\bm{e}_z\}$ で展開します．

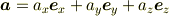
$\bm{a} &=a_x \bm{e}_x + a_y \bm{e}_y + a_z \bm{e}_z$

座標系がデカルト座標系(直線直交座標系)の場合が代表例ですね．成分は正規直交性により

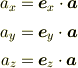
$a_x &= \bm{e}_x\cdot\bm{a}\\a_y &= \bm{e}_y\cdot\bm{a}\\a_z &= \bm{e}_z\cdot\bm{a}$

となります．

本来は成分表示は一次独立なベクトルの任意の組 $\{\bm{g}_1,\bm{g}_2,\bm{g}_3\}$ (単位ベクトルでもないし，互いに直交もしない)を基底にしたものでも

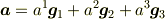
$\bm{a} &=a^1 \bm{g}_1 + a^2 \bm{g}_2 + a^3 \bm{g}_3$

できますが，成分の導出が正規直交基底のようにはいきません．

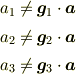
$a_1 &\ne \bm{g}_1\cdot\bm{a}\\a_2 &\ne \bm{g}_2\cdot\bm{a}\\a_3 &\ne \bm{g}_3\cdot\bm{a}$

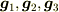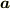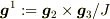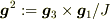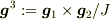
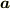# ここで， $\bm{g}_1,\bm{g}_2,\bm{g}_3$ を $\bm{a}$ に内積する代わりに，「逆基底」 $\bm{g}^1:=\bm{g}_2\times\bm{g}_3/J$ , $\bm{g}^2:=\bm{g}_3\times\bm{g}_1/J$ , $\bm{g}^3:=\bm{g}_1\times\bm{g}_2/J$ $(J=\bm{g}_1\cdot(\bm{g}_2\times\bm{g}_3))$ を $\bm{a}$ に内積すると成分が計算できます．このように，正規直交基底でなくとも成分計算はできますが，「双対な基底」あるいは「逆基底」を導入しなければいけません．(cf. 斜交座標系)

ですから，普通は正規直交基底が使われます．軸座標系や極座標系のような曲線直交座標系では座標軸が常に直交するので，正規直交基底を使うことができます．正規直交基底のメリットは長さ(内積)や外積，成分表示が簡単であることですね．

しかし，微分がはいると話はややこしくなります．

スカラー場 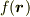$f(\bm{r})$ の勾配やベクトル場 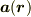$\bm{a}(\bm{r})$ の回転は直線直交座標系では

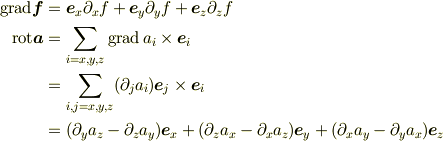
$\mathrm{grad}\bm{f} &= \bm{e}_x \partial_x f + \bm{e}_y \partial_y f + \bm{e}_z \partial_z f\\\mathrm{rot}\bm{a} &= \sum_{i=x,y,z} \mathrm{grad}\,a_i \times \bm{e}_i\\&= \sum_{i,j=x,y,z} (\partial_j a_i) \bm{e}_j \times \bm{e}_i\\&= (\partial_y a_z - \partial_z a_y)\bm{e}_x+ (\partial_z a_x - \partial_x a_z)\bm{e}_y+ (\partial_x a_y - \partial_y a_x)\bm{e}_z$

ですが，たとえば，軸座標系ではこのように簡単にはなりません．(教科書を参照してください)．これは，座標の格子の幅や方向が位置とともに変わるためで，特に回転は

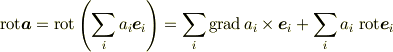
$\mathrm{rot}\bm{a} &= \mathrm{rot}\left(\sum_i a_i\bm{e}_i\right)= \sum_i \mathrm{grad}\,a_i \times \bm{e}_i+ \sum_i a_i~ \mathrm{rot}\bm{e}_i$

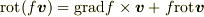の最後の式の第2項の様に，基底ベクトルの空間変化を考えなければいけないからです．(基底ベクトルは $\theta$ に依存しています．なお，上の式では $\mathrm{rot}(f\bm{v}) = \mathrm{grad}f\times\bm{v} + f \mathrm{rot}\bm{v}$ の公式を使っています．)

結局，曲線直交座標系では，正規直交基底は微分とはなじみません．ま，公式集をみればよいのですが，相対論のように任意の曲線(非直交)座標系を使った方がよい理論では，そもそも正規直交基底は使えません．

それで，正規直交基底を捨てて，微分になじみのよい基底を探します．

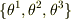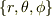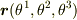一般の曲線座標系 $\{\theta^1,\theta^2,\theta^3\}$ を考えます(極座標系なら $\{r,\theta,\phi\}$ です)．位置ベクトル $\bm{r}$ は座標の関数 $\bm{r}(\theta^1,\theta^2,\theta^3)$ で表されます．

微分になじみのよい基底ということで，座標と位置の間の微分で作られる以下の2種類の基底を考えます．一つ(基底)は

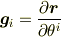
$\bm{g}_i = \frac{\partial \bm{r}}{\partial \theta^i}$

からなる組で，もう一つ(双対基底)は

$\bm{g}^i = \nabla \theta^i (= \frac{\partial \theta^i}{\partial \bm{r}})$

からなる組です．

(前者は座標軸(曲線)の接ベクトルであり，座標軸(曲線)を座標(曲)面群で切り取った線分の長さが大きさとなります．後者は座標(曲)面群の法線ベクトルであり，面群の間隔の逆数の大きさを持ちます．) 直線直交座標系 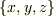$\{x,y,z\}$ では2つの表現は 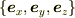$\{\bm{e}_x,\bm{e}_y,\bm{e}_z\}$ に一致します．

これらは正規直交基底ではないので

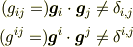
$(g_{ij}= )\bm{g}_i\cdot\bm{g}_j &\ne \delta_{i,j}\\(g^{ij}= )\bm{g}^i\cdot\bm{g}^j &\ne \delta^{i,j}$

なのですが，

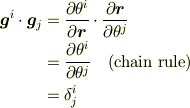
$\bm{g}^i\cdot\bm{g}_j &= \frac{\partial \theta^i}{\partial \bm{r}} \cdot \frac{\partial \bm{r}}{\partial \theta^j} \\&= \frac{\partial \theta^i}{\partial \theta^j} \quad(\text{chain rule})\\&= \delta^{i}_{j}$

がなりたちます．

これを使えばベクトル

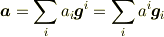
$\bm{a}=\sum_i a_i \bm{g}^i = \sum_i a^i \bm{g}_i$

の成分は

$a_i &= \bm{g}_i \cdot \bm{a}\\ a^i &= \bm{g}^i \cdot \bm{a}$

と表示できます．これがベクトル 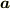$\bm{a}$ の共変成分と反変成分です．

複数の基底を使うのはややこしいですが，反面，微分計算が楽になります．

例えば

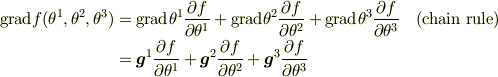
$\mathrm{grad}f(\theta^1,\theta^2,\theta^3) &= \mathrm{grad} \theta^1\frac{\partial f}{\partial \theta^1} + \mathrm{grad} \theta^2\frac{\partial f}{\partial \theta^2} + \mathrm{grad} \theta^3\frac{\partial f}{\partial \theta^3} \quad\text{(chain rule)}\\&= \bm{g}^1 \frac{\partial f}{\partial \theta^1} + \bm{g}^2 \frac{\partial f}{\partial \theta^2} + \bm{g}^3 \frac{\partial f}{\partial \theta^3}$

となり，勾配の共変成分は 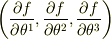$\left(\frac{\partial f}{\partial \theta^1}, \frac{\partial f}{\partial \theta^2},\frac{\partial f}{\partial \theta^3}\right)$ のように，直線直交座標系とおなじ表現になります． (なお，微小変位は

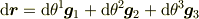
$\mathrm{d}\bm{r} = \mathrm{d}\theta^1 \bm{g}_1 + \mathrm{d}\theta^2 \bm{g}_2 + \mathrm{d}\theta^3 \bm{g}_3$

となるのが同様に導けます．

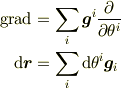
$\mathrm{grad} &=\sum_i \bm{g}^i \frac{\partial}{\partial \theta^i}\\\mathrm{d}\bm{r} &=\sum_i \mathrm{d}\theta^i \bm{g}_i$

という対応ですが，逆にこうなるように 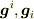$\bm{g}^i, \bm{g}_i$ を定義すると考えてもいいです．)

回転は

$\mathrm{rot}\bm{a} &= \mathrm{rot}\left(\sum_i a_i\bm{g}^i\right)= \sum_i \mathrm{grad}\,a_i \times \bm{g}^i+ \sum_i a_i~ \mathrm{rot}\bm{g}^i$

で最後の項は

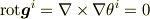
$\mathrm{rot}\bm{g}^i=\nabla\times\nabla\theta^i=0$

で消えるので，やはり，直線直交座標系とおなじ表現

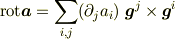
$\mathrm{rot}\bm{a} &= \sum_{i,j} (\partial_j a_i)~\bm{g}^j \times \bm{g}^i$

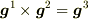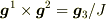
になります． (ただし，この後の計算で $\bm{g}^1\times\bm{g}^2=\bm{g}^3$ ではなく， $\bm{g}^1\times\bm{g}^2=\bm{g}_3/J$ $(J=\bm{g}_1\cdot(\bm{g}_2\times\bm{g}_3))$ であることが違ってきます．)

このように導入した基底(＝自然基底)では微分計算が直線直交座標系とほとんどおなじ表現になり見通しが良くなります． # 体積要素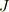あるいは密度量 1/J を考慮しなければいけないのが若干違います．

最後に座標変換の話をして終わります．曲線座標系 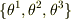$\{\theta^1,\theta^2,\theta^3\}$ を別の曲線座標系 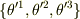$\{\theta'^1,\theta'^2,\theta'^3\}$ に変換することを考えます．自然基底のもう一つの長所は座標変換が自然な式で書けることです．基底の座標変換は

$\bm{g}^{i} &= \nabla \theta^i\\&= \sum_j \frac{\partial \theta^i}{\partial \theta'^j}\nabla \theta'^j \quad\text{(chain rule)}\\&= \sum_j \frac{\partial \theta^i}{\partial \theta'^j} \bm{g}^{j'}$

と一般の場合でもきれいに書けます．

これを使うと

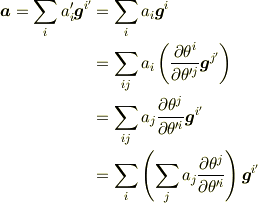
$\bm{a} = \sum_i a'_i \bm{g}^{i'} &= \sum_i a_i \bm{g}^{i}\\&= \sum_{ij} a_i \left(\frac{\partial \theta^i}{\partial \theta'^j} \bm{g}^{j'}\right)\\&= \sum_{ij} a_j \frac{\partial \theta^j}{\partial \theta'^i} \bm{g}^{i'}\\&= \sum_{i} \left(\sum_j a_j \frac{\partial \theta^j}{\partial \theta'^i}\right) \bm{g}^{i'}$

より

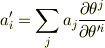
$a'_i = \sum_j a_j \frac{\partial \theta^j}{\partial \theta'^i}$

という関係式が得られます．これを共変成分の座標変換則とよび，逆にこの変換則に従うものを共変ベクトル(成分)とよぶのです．反変ベクトル(成分)も同様に

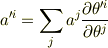
$a'^i &= \sum_j a^j \frac{\partial \theta'^i}{\partial \theta^j}$

を満たすものです．

(最終変更 07年09月20日)

Re: 反・共ベクトル

zoro さんのレス (2007/08/07(Tue) 17:30)

割り込み，失礼します．

toorisugari no Hiroさん，

素人からみても，少し判って来る様な予感をします．

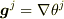＞基底として最初に下の2種類を考えます．＞一つは＞ $\bm{g}_i = \frac{\partial \bm{r}}{\partial \theta^i}$ ＞もう一つは＞ $\bm{g}^j = \nabla \theta^j$ ＞です．

ここら辺を，もう少し噛み砕いていただけると有難いです．勿論，急ぎませんが．

Re: 反・共ベクトル

toorisugari no Hiro さんのレス (2007/08/07(Tue) 18:03)

> ここら辺を，もう少し噛み砕いていただけると有難いです．

どういう方向でかみ砕けばいいでしょうか?

Re: 反・共ベクトル

zoro さんのレス (2007/08/07(Tue) 20:07)

まだ，私も判らん状態ですので，質問自体がぐらついていますが...(笑)．

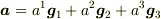
＞一次独立なベクトルの組 $\{\bm{g}_1,\bm{g}_2,\bm{g}_3\}$ を基底にしたものでも＞ $\bm{a} &=a^1 \bm{g}_1 + a^2 \bm{g}_2 + a^3 \bm{g}_3$

としただけで，＞ $\bm{g}_i = \frac{\partial \bm{r}}{\partial \theta^i}$

と書ける，というか定義するというか，何らかの説明というか，解釈というかがないのでしょうか？少なくとも，数学音痴にとっては，深遠なギャップに見えています．

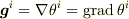
次に，＞ $\bm{g}^i = \nabla \theta^i = \mbox{grad}\,\theta^i$

と見て良いなら，曲線座標系の成分， $\theta^i$ が一定の曲面にたいする法線ヴェクタを示す様に感じます．

結局，「別々に定義した基底が直交する」というのが，容易にイメージ出来ません．

恐らく，自分のばあい，通常の常識で皆さんがお持ちな何かの認識が出来ていないように推察されますが，いまだミッシング・リングなのでしょうね．

〜〜〜待てよ，こう書いてみると， $\bm{g}_i = \frac{\partial \bm{r}}{\partial \theta^i}$ は，偏微分する座標の接線ヴェクタ？？？，でしょうか？

Re: 反・共ベクトル

toorisugari no Hiro さんのレス (2007/08/07(Tue) 20:36)

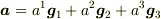>> 一次独立なベクトルの組 $\{\bm{g}_1,\bm{g}_2,\bm{g}_3\}$ を基底にしたものでも >> $\bm{a} &=a^1 \bm{g}_1 + a^2 \bm{g}_2 + a^3 \bm{g}_3$ > としただけで， >> $\bm{g}_i = \frac{\partial \bm{r}}{\partial \theta^i}$ > と書ける，というか定義するというか，何らかの説明というか，解釈というかがないのでしょうか？恐らく，数学音痴にとっては，深遠なギャップに見えています．

一つの面上にない三つの任意のベクトルは，一次独立で，このベクトルの組の線形和で任意の3次元ベクトルを

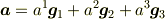
$\bm{a} &=a^1 \bm{g}_1 + a^2 \bm{g}_2 + a^3 \bm{g}_3$

表現できます．

空間次元とおなじ個数の一次独立なベクトルからなる組を基底といいます．

基底は何でも良いのです．次元と同数で一次独立であれば．今，座標系にマッチした基底を探しているのですから

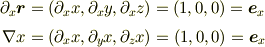
$\partial_x \bm{r} &=(\partial_x x, \partial_x y, \partial_x z) = (1,0,0) = \bm{e}_x\\\nabla x &=(\partial_x x, \partial_y x, \partial_z x) = (1,0,0) = \bm{e}_x$

正規直交基底を拡張したものとして，自然基底は素直だと思うのですが．．．．

> 結局，「別々に定義した基底が直交する」というのが，容易にイメージ出来ません．

これは数式で理解してもらった方が早いです．

どうしても幾何学的に理解したいのでしたら，これは面の綾と面間の間隔(=grad)の関係ですから，gradの幾何学的感覚をつかんでもらえればいいのですが．．．

平行六面体の格子を考えます．

gradは面の法線と平行です．面の法線と面の綾は直交しますよね．ですから「別の方向に相当するベクトルの組は直交する」のです．

また，gradは面と，その面に相対する面の間の距離に反比例します．ふたつの面を結ぶ線(これは別の面の綾になっています)は，面の法線と直交はしませんし，相対する距離に比例しますから，gradと線ベクトルの内積は1になります．

> 待てよ，こう書いてみると， $\bm{g}_i = \frac{\partial \bm{r}}{\partial \theta^i}$ は，偏微分する座標の接線ヴェクタ？？？，でしょうか？

そうっすよ．座標軸に平行なベクトルに相当するものです．

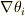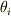反面 $\nabla \theta_i$ は $\theta_i$ の等値面(「座標面」)に垂直なベクトルで等値面間隔に反比例します．

ここらへんは斜交座標系を勉強されると良いと思います．

Re: 反・共ベクトル

zoro さんのレス (2007/08/07(Tue) 23:19)

＞今，座標系にマッチした基底を探しているのですから＞式略＞を拡張したものとして，自然基底は素直だと思うのですが．．．．

なるほど，88%位判ってきました．

斜交座標と聞くとアレルギーがあるのですが，盾矛さんのオリジナルの質問からすれば，ピタリの設定ですね．

どうしても，頑迷な頭なので「直交座標系」で考えてしまうので，

$\bm{g}_i = \bm{g}^i$

となりそうで，違和感があるのだと思います．

2次元で回転系を相手に，少し具体的に考えてみる事にします．横からの質問は終了します，有り難うございました．

Re: 反・共ベクトル

zoro さんのレス (2007/08/08(Wed) 18:01)

自己引用させて戴きますと，たとえ斜交座標でなて，直交座標系であっても，

＞「直交座標系」で考えてしまうので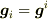，＞ $\bm{g}_i = \bm{g}^i$ ＞となりそうで，違和感があるのだと思います．

逆に言えば，直交座標系においても，「共変ベクトルと反変ベクトル」に対応するなんらかの性質が在り得ないかと思います．ただ，この問いかけは参考に書いただけですので，お気になさらずに，本道の論議をお願いします．

Re: 反・共ベクトル

盾矛さんのレス (2007/08/08(Wed) 23:37)

掲示板が一人歩きしていますが・・・

ありがとうございました．丸暗記していて，もやもやしていた部分がすっきりしました．

ようやく，「なぜ」に対する答えが見つかりました．

長くてわかりやすい説明をありがとうございました．

Re: 反・共ベクトル

toorisugari no Hiro さんのレス (2007/08/09(Thu) 07:50)

> 直交座標系においても，「共変ベクトルと反変ベクトル」に対応するなんらかの性質が在り得ないかと思います．

一言で言ってしまうと，接ベクトルと，その双対ベクトルである余接ベクトルということなんですが．．．身も蓋もないですかね．

> 掲示板が一人歩きしていますが・・・

掲示板は議論の場という意味で，正しい姿です．

[home] [掲示板] [ページの先頭]