山猫 さんの書込 (2007/08/02(Thu) 11:05)

なぜ E=hv という式からエネルギーがとびとびの値しかとれないということになるのでしょうか？

山猫 さんのレス (2007/08/03(Fri) 10:09)

ダメでしょうか… この式からエネルギーが飛び飛びの値しかとらないことがわかり， 「量子」という概念が生まれた と書いてあったのですが， なぜ飛び飛びになるのですか？

zoro さんのレス (2007/08/03(Fri) 11:27)

山猫さん，不思議とプランクの式の成立過程を思い出せなくて...．

ただ，この式だけでは「エネルギーが飛び飛びの値しかとらない」とは言えないと思います．このエネルギーをもった粒子という解釈ができるという事だと思います．

他方，エネルギーが飛び飛びというのは，ある一定の温度の容器に囲まれた中で，熱的に平衡となった光がどのような分布をするか，直裁にいえば，溶鉱炉のなかの温度を正確に量る為に，光の周波数分布を出そうとしたのだと思います．これを一口に，黒体輻射の問題とも言いますが，溶鉱炉の大部分は光が漏れないので，極端にいって，光の出口が無い極限として「黒体」と言ったのだろうとおもいます．

此処から先は，うろ覚えモードですので，間違えているかも知れません．

上の意味の状態を古典的電磁波で，記述する為には，例えば，辺の長さがLであるような立方体を考えて，計算する事になります．この計算は結構めんどうですが，時間的に平衡なので，定在波，例えば，風呂場で手を強く上下すると，一定の波出て来たりしますよね．

このように，定在波の波長は，飛び飛びになります．そこで，プランクさんは，有限の大きさの黒体容器での飛び飛びのエネルギー分布をもとに其のエネルギーに対する状態の数を算定して，さいごに容器の大きさを無限にして，飛び飛びの効果を取るつもりだったのが，なんと無限にすると実験に合わなくなったという，感じだったと思います．

そろそろ，学生さん達が本格的な夏休みモードだと思うので，本格的な説明はそれらの方々にお願いします，ペコリ．

リッチ さんのレス (2007/08/03(Fri) 19:07)

こんにちは． ご指摘のプランクの式ですが，もともとはE=nhvであります．ここでnは整数，hはプランク定数，vが振動数になります．これでしたらいわゆる「量子化」されている式になっています．参考書には確かにE=hvとしか書いていないことが多いかもしれませんが，その際に「エネルギーの最小単位（すなわちn=1)」といった記述がないでしょうか．自分の持っているものにはそう書いてあります． これで解決されたでしょうか？

山猫 さんのレス (2007/08/04(Sat) 00:19)

なるほどそうだったんですか． nは何を指しているのかはわかりませんが，振動数vの光のエネルギーは必ずhvの整数倍になっているということなんですね． ありがとうございました

zoro さんのレス (2007/08/04(Sat) 01:14)

リッチさん，初めまして．

＞もともとはE=nhvであります．

なるほど，そのような解釈であれば，私は大変な間違いをしていた事になります．宜しければ，其の解説の出典をお教え下さいませんか？

リッチ さんのレス (2007/08/04(Sat) 16:49)

自分は化学を専攻する学生なので，物理化学の専門書になりますがよろしいでしょうか？ 東京化学同人「物理化学−分子論的アプローチ」マッカーリ・サイモン著 を参照致しました．本書には「プランクは振動子のエネルギーはとびとびの値であり，振動数の整数倍に比例する，すなわちE=nhv，という革命的な仮定を置いた」と記されています．この本はアマゾンなどでも評価が高く，京都大学などでもテキストとして用いられています．もし宜しければ書店等でご覧下さい．

yama さんのレス (2007/08/04(Sat) 18:48)

プランクの考察については朝永振一郎「量子力学?」にも説明されています．

zoro さんのレス (2007/08/04(Sat) 20:12)

皆さん，先にお詫びします．

私は，「プランクの式」を拝見した時に，黒体輻射の「プランクの法則，Planck's law」だと勘違いしました．yahooで「黒体ウィキペディア」で調べるうちに下記のサイトに気が付きましたが，疲れて寝てしまい，ご報告が遅れました．

１）Planck's law

• http://en.wikipedia.org/wiki/Planck%27s_law_of_black_body_radiation

２）Planck's original 1901 paper: On the Law of Distribution of Energy in the Normal Spectrum

• http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Planck-1901/Planck-1901.html

資料２）は，見難いのですが，元報の英語訳のようですのでご参考にされていただければ幸いです．ただ前半が熱力学的な考察なので，熱力学を理解できないと読めませんが(泣)．

リッチさん，

＞プランクは振動子のエネルギーはとびとびの値であり，振動数の整数倍に比例する，すなわちE=nhv，という革命的な仮定を置いた」

そうですか，私は，これを言ったのはアインシュタインさんだと勘違いしました．プランクさんが，光子(ボゾン)の振動エネルギの解を最初に指摘したのですね．

ご紹介の図書も探してみます．有り難うございます．

yamaさん，

＞プランクの考察については朝永振一郎「量子力学?」

一年生の夏休みの宿題が，「上記図書を完読して感想文をかけ」だったのですが，不得意な熱力学で，この部分を読み違えたかとおもいます．

とは言え，再度，拝見してみますね．

yama さんのレス (2007/08/04(Sat) 21:18)

>＞プランクは振動子のエネルギーはとびとびの値であり，振動数の整数倍に比例する，すなわちE=nhv，という革命的な仮定を置いた」

>そうですか，私は，これを言ったのはアインシュタインさんだと勘違いしました．プランクさんが，光子(ボゾン)の振動エネルギの解を最初に指摘したのですね．

これについては，zoroさんが挙げられた資料２の中に次のように書かれていますね．

§10. If we apply Wien's displacement law in the latter form to equation (6) for the entropy S, we then find that the energy element ε must be proportional to the frequency v, thus:

ε = hv

and consequently:

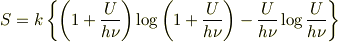
here h and k are universal constants.

zoro さんのレス (2007/08/04(Sat) 21:55)

yamaさん，

＞これについては，zoroさんが挙げられた資料２の中に次のように書かれていますね．

やはり，追求されました(汗)．

プランクの公式の成立過程を現段階では思い出せませんが，少なくとも，この場合光子エネルギ(ないし，光の振動数)のスペクトルを論じているので，ε＝hνとする時には，その整数倍nを含めると，とても重複したスペクトルになると思いました．

他方，エントロピーの展開部分は，熱力学の落ちこぼれには，「豚に真珠」の有様で，理解出来ません．この様子では，あと一年ほどは掛かると思います．

でも，1901年のだんかいで，

＞here h and k are universal constants.

と指摘されているのは，とても驚くべきだろうと感じました！！！...！！！．前期量子力学は，とてもビビッドな世界だったのでしょうね．

21世紀の前半である今日，物理でも数学のように過去の論文にヒントを得るのも良いかも知れませんね．

小林＠那須 さんのレス (2007/08/06(Mon) 09:20)

>E=hv という式からエネルギーがとびとびの値しかとれないということになるのでしょうか？

このような言い方に私も惑わされました．「調和振動子の固有エネルギーが E = n h ν ...」ならば理解できますが，上のような表現では誤解を招くだけです．こんな騙しに近い表現には拘らずに，ちゃんとした量子力学の教科書と，自分で格闘することを薦めます．同時に，この疑問を抱き続け，最終的に自分で自分に回答することを望みます．

E=h ν の式は Einstein が光電効果の説明で使い出しました．(これで Novel 賞を与えられました)．「振動数 ν の光が h ν のエネルギーを持つ」という一見単純な話ですが，この式の物理的意味を理解するのは簡単ではありません．まして「E=hv という式」だけからエネルギーがとびとびの値しかとれない」なんてことが導けるなんて思うべきではありません．

これだけでは批判だけになってしまうので，私の E = h ν 解釈を書いてみます．

E=h ν の式の凄い点は，光という広がりを持った波が電子という小さな粒子に，弾丸のように全エネルギーを集中させて与えられると主張している点です．

可視光の波長は 1`μm 程度です．一方で原子の格子間隔は 1`nm 以下です．光のエネルギーを与えられる電子は，この原子それぞれより供給されます．光電効果では，このうちの電子一個だけに，光子一個の全エネルギー h ν を与えられます．

ここで 1`nm を 1`meter に拡大して考えて見ます．そして電子をボールに例え，光のエネルギーを雨に例えてみましょう．1`km^2 の地面に 1`meter 間隔で電子のボールを並べたと考えてみましょう．この 1`km^2 の地面に一様に光エネルギーの雨を降らしたとき，一個の電子(ボール)にだけ雨（エネルギー）が集中して電子(ボール)が飛び出すというのが E = h ν の式が主張していることです．不思議な話ですが，光電効果で現実に起きていることです．

量子力学で「エネルギーがとびとびになる」，「波動性と粒子性がある」とか言われますが，「エネルギーが集中できる」といったほうが良いと思っています．それを象徴的に表しているのが E = h ν であり，上の雨とボールの例えです．

Einstein が量子力学を理解できなかったなどと言われることがありますが，それは全くの誤りです．上の雨とボールの例えで説明したような常識では受け入れられない E = h ν を主張できた Einstein は量子力学の本質を的確に理解していたと主張します．

E = h ν の式の物理的意味をどのように解釈しているかは，量子力学をどのように理解しているかの良い標識になると思います．教科書を丸暗記するだけで済ます方たちでは E = h ν の式の難しさなど感じられないでしょう．この式で Einstein がノーベル賞を得た理由など理解できないでしょう．

山猫さんも，このような primitive な疑問を持ち続けることを望みます．そして量子力学を自分なりに理解した後に，自分で自分に回答してみてください． そして山根さんの E = h ν の解釈を書いてくれることを希望します．