中心力

中心力

song さんの書込 (2007/07/30(Mon) 23:00)

中心力が保存力である証明はどうすればいいですか？また， 摩擦力が保存力でないことの証明はどうしたらいいですか？

Re: 中心力

zoro さんのレス (2007/07/31(Tue) 01:54)

songさん，初めまして．

文面から，大学生だと仮定して，すこし書いてみます．基本的に運動の方程式；

m\frac{\mbox{d}\vec v(t)}{\mbox{d} t} = \vec f, \tag{1}

に於いて，右辺の外力によってどのような特徴が考えられるかが，課題ですね．

●ーーーーーーーーーーーーーー● ●（１）中心力が保存力の場合● ●ーーーーーーーーーーーーーー●

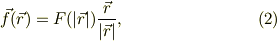
\vec f(\vec r) = F(|\vec r|)\frac{\vec r}{|\vec r|}, \tag{2}

と考えて良いですね．

今，空間の原点は含まない別々の2点A,Bを考えます．其の途中にある別々の2点，C,Dを考えます．

<pre> 三次元デカルト座標系Oxyz と内部の独立した空間点，A,B,C, and D

B . * . . . . . . D * . . * C z . . . . ↑ *. . ｜A ｜ 原点O ・ーー→y ／

\ \swarrow

</pre>

保存力であれば，2点A,Bを繋ぐ任意の仕事積分は，その経路依らずに一定．

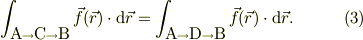
\int_{\mbox{A}\to \mbox{C} \to \mbox{B}}\vec f(\vec r)\cdot \mbox{d}\vec r = \int_{\mbox{A}\to \mbox{D} \to \mbox{B}}\vec f(\vec r)\cdot \mbox{d}\vec r. \tag{3}

右辺の積分の逆経路を考えると，符号が逆転するだけですから

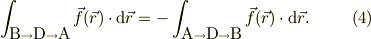
\int_{\mbox{B}\to \mbox{D} \to \mbox{A}}\vec f(\vec r)\cdot \mbox{d}\vec r = -\int_{\mbox{A}\to \mbox{D} \to \mbox{B}}\vec f(\vec r)\cdot \mbox{d}\vec r. \tag{4}

だから，式(3),(4)を辺々加えると，経路を一周すると；

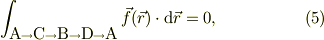
\int_{\mbox{A}\to \mbox{C} \to \mbox{B} \to \mbox{D} \to \mbox{A}}\vec f(\vec r)\cdot \mbox{d}\vec r = 0, \tag{5}

と言った特徴があります．以下，具体的に考えましょう．まず，式(2)を式(3)の積分に代入してみますと，

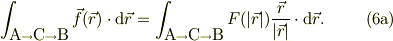
\int_{\mbox{A}\to \mbox{C} \to \mbox{B}}\vec f(\vec r)\cdot \mbox{d}\vec r &= \int_{\mbox{A}\to \mbox{C} \to \mbox{B}} F(|\vec r|)\frac{\vec r}{|\vec r|}\cdot \mbox{d}\vec r. \tag{6a}

此処で，ベクトルの内積公式，

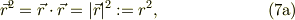
\vec r^2 = \vec r \cdot \vec r = |\vec r|^2 := r^2, \tag{7a}

この左右の微分を考えれば，

2\vec r \cdot \mbox{d}\vec r = 2r\mbox{d}r, \tag{7b}

という恒等式が成立するから，式(6b)は，スカラ積分に変形出来ます；

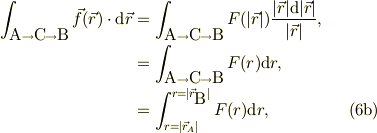
\int_{\mbox{A}\to \mbox{C} \to \mbox{B}}\vec f(\vec r)\cdot \mbox{d}\vec r &= \int_{\mbox{A}\to \mbox{C} \to \mbox{B}} F(|\vec r|)\frac{|\vec r|\mbox{d}|\vec r|}{|\vec r|}, \\&= \int_{\mbox{A}\to \mbox{C} \to \mbox{B}} F(r)\mbox{d}r, \\&= \int_{r=|\vec r_{A}|}^{r=|\vec r_{\mbox{B}}|} F(r)\mbox{d}r,\tag{6b}

積分の始点Aと終点Bの原点からの長さだけの関数となっており，中間CとかDに依りません．まさに式(3)を満たします．

■ーーーー■ ちょっと脱線 ■ーーーー■

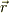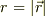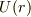位置ベクトル \vec r の絶対値 r=|\vec r| の関数 U(r) の微分を考えます．

当たり前ですが，

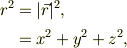
r^2 &=|\vec r|^2,\\&= x^2 + y^2 +z^2,

ですから，この微分は

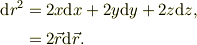
\mbox{d}r^2 &= 2x\mbox{d}x +2y\mbox{d}y + 2z\mbox{d}z, \\&= 2\vec r \mbox{d} \vec r.

そこで，rの関数の全微分が次のように表す事が出来る；

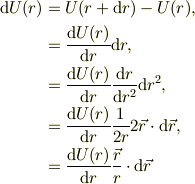
\mbox{d}U(r) &= U(r + \mbox{d} r) -U(r),\\ &= \frac{\mbox{d}U(r)}{\mbox{d} r}\mbox{d}r,\\&= \frac{\mbox{d}U(r)}{\mbox{d} r}\frac{\mbox{d}r}{\mbox{d}r^2}\mbox{d}r^2,\\&=\frac{\mbox{d}U(r)}{\mbox{d} r}\frac{1}{2r}2\vec r \cdot \mbox{d} \vec r,\\&=\frac{\mbox{d}U(r)}{\mbox{d} r}\frac{\vec r}{r} \cdot \mbox{d} \vec r

全微分が存在すれば，其の積分を得る事ができる．またこれらを，式(6a,b)と比較してみて下さい．

■ーーーーーーー■ 微小領域の一周積分←工事中 ■ーーーーーーー■

ある有限な領域での一周積分を考える時に，

（２）摩擦力が保存力でないこと

\vec f = -k\vec v \tag{a}

などで「（１）の条件に背く」といった感じで考えるのはどうでしょうか？

■現在，工事中．

Re: 中心力

song さんのレス (2007/07/31(Tue) 03:06)

おつかれのところありがとうございました．

Re: 中心力

zoro さんのレス (2007/07/31(Tue) 12:44)

途中までですが，No.17208 の式(6b)の説明まで書いてみました．

こんな感じで判りますか？