円運動の加速について・・

円運動の加速について・・

飲みすぎ さんの書込 (2007/07/28(Sat) 09:14)

テニス好きの会社員です． 最近良く考えている円運動について色々とコメントをいただきたく， こちらの掲示板への書き込みを思い立ちました．

内容を以下に記述します． お手数かとは存じますが，どうか宜しくお願い致します． −−−−−

■円運動の速度をどうすれば効率よく加速できるのか・・・

・よくスポーツの世界では体の「軸」の意識が重要と言われます．

・野球でバットを振ったり，ゴルフでクラブを振ったり， テニスでラケットを振ったり・・等々にて，道具に円運動をさせつつ 体軸がブレない様なスイングを求められ，実際上級者ほど体軸が しっかりしている様に見えます．

・ここで，円運動について物理的に考えてみますと・・・

?まず，ある速度の物体に円運動をさせる場合は， 必ず中心に向かって力（V^2/R）を掛け続ける必要があります． ↓ ?但し，円運動をする物の速度を加速しようとすると， 物の速度方向の力（円の接線方向の力成分）が必要になります． ↓ ?つまり，円運動の中心軸から入力する力では， 円運動をする物の速度は上がらない・・・となります．

もしかすると，一般的に体軸の重要性について 考えを改める必要性があるのかもしれません．

★例えば，ヒモの先端に重りを付けたものを手で振り回す時， ★円運動をする重りの速度を上げようとすると， ★円運動の中心から外れた位置から引っ張るような感じで ★加速させていきます． ★ ★この円運動を加速させていく現象は何なのでしょうか． ★物理的に名称や理論のようなものがあるのでしょうか． ★また，効率良い円運動の加速方法はあるのでしょうか．

どうかどうか，宜しくお願い致します．m(__)m

Re: 円運動の加速について・・

zoro さんのレス (2007/07/28(Sat) 16:37)

飲みすぎさん，初めまして．

私は，体のリハビリテーションで水泳を始めたのですが，今は，水泳にハマっています．昨年から，脳のリハビリテーションでこの掲示板を利用させていただいています．

体軸の重要性は，野球に限らず，運動や武道など，更に言えば，日常生活での体使いまで，共通した現象だと思います．腰の上に脊柱があり，その上に頭があり，脊柱の全面に胸郭とうボックスが付着しています．腰の下には脚部と足がついて自立している訳ですね．また，胸骨の裏に，肩甲骨があり，そこから腕がでて手に至ります．

水泳でも，クロールと背泳は，体軸についての捻れ運動(ローリング)，肩や腰についてのヨーイングが腕や脚の運動と連動することで，効率の良い泳ぎが出来るのだろうと推測しています．

＃まだ体の動きよりも，机上検討の方が勝っているので(苦笑)．

さて，ご質問は，

（１）等速円運動を保持する原因は何か？ （２）円運動で加速するのは何か？ （３）特に効率の良い加速とはなにか？

（１）,（２）はご自分で結論を出されているようにも思えます．疑問点があれば，もう少し，詳しく書かれていただければ，幸いです．

（３）は，一般論では解決出来ないと思います．これも具体論があればお教え下さい．でも，野球の解説書を見られた方が速い様な気もします．もし解説書の此処が判らないという点があれば，こちらも考え易くなります．

＃例えば， ＃ 野球やゴルフのスウィング ＃ ハンマー投げの動作 ＃ 野球の投球 ＃ ボクシングのアッパー・カット

また水泳の経験から推測すると，足が地面と摩擦力でホールドして，その地面からの抗力を骨と関節で腰に伝え，その腰に直接接続している脊柱から腕までの連続で，手に達するので，物理的には結構難しいので，如何に良いモデルを作るか，いっその事，ロボットの解析技術に走ったりと，色々な方法がありそうですね．

Re: 円運動の加速について・・

飲みすぎ さんのレス (2007/08/01(Wed) 21:06)

＞＞zoroさん

ご回答いただき，ありがとうございました． （お礼の返答が遅れてしまい済みません．．）

>（１）等速円運動を保持する原因は何か？ >（２）円運動で加速するのは何か？ >（３）特に効率の良い加速とはなにか？

これらの件について現在自分が考えていることは， 全然大したことはなくて，以下の様なことです．

●スピードの速い物体を更に加速しようとする時， 速度方向に力の入力が困難な場合でも，速度方向とは ベクトルの異なる方向には少しの力でも入力は容易． ↓ （ということを利用して） ↓ 物体を引いて速度を発生させ，そのまま回転運動に移行して， 回転の中心とは少しずれた位置から物体を引き続ければ， 遠心力の張力＋αの小さな力で大きな速度を発生できるのではないか．

●効率の良い円運動の加速方法については， 身近な参考例として，紐の先に重りを付けたものを ビュンビュン振り回す時のことをよく観察すれば 何か解答が見付かるのではないか．

−−−−−−−− 追伸，

●もし，これに関連しそうなスポーツ系の解説書で参考になりそうな ものをご存じであれば，是非ご教示をお願いします．m(__)m

●回転する物が質点の場合，角運動量保存則から，回転半径を 短くすれば重りの速度が上がります．（(m・v)・r＝(m・v')・r'）

でも，回転するものが剛体の場合，角運動量保存則から， 回転半径を短くしても先端の速度は変化しないような 気がするのですが（以下理由），何方かに正／誤を ご教示いただきたく，どうかお願い致します．

M（剛体の重さ）

←V（先端の速度） ｜ ｜L（剛体の長さ） ｜ ｜ω（角速度） ・（回転の中心）

（角運動量）＝(∫(M/L)・x^2dx)・ω（←積分は，0〜L） ＝(1/2)・M・L・ω

Lを変化させてもMは変化しない場合， 角運動量保存則から，

(1/2)・M・L・ω＝(1/2)・M・L'・ω' よって，L・ω＝L'・ω'＝Ｖ（Lを変化させてもＶ一定） ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

これは正しいのでしょうか・・・・．

Re: 円運動の加速について・・

zoro さんのレス (2007/08/01(Wed) 22:51)

私は，水泳の分析の興味から，下記の図書を拝見しました．

ピッチングの正体 手塚 一志・著 ベースボール・マガジン社 1998

アマゾンのサイトでは，この著者の方のその他の本もあるようです．

それらを図書館でご覧になって，判らない所を，再度書かれれば，説明出来るかも知れませんね．

Re: 円運動の加速について・・

Joh さんのレス (2007/08/01(Wed) 23:16)

zoroさん＞

＞また，胸骨の裏に，肩甲骨があり，そこから腕がでて手に至ります．

肩甲骨はほかの骨に直接は接続していません．腕は鎖骨を通じて，背骨から生えています．揚げ足取りのようで申し訳ないですが，しかし，腕の長さを鎖骨も含めてイメージすると，その分長く使えて色々得です．多分，水泳でも役に立つと思ったので指摘させていただきました．

Re: 円運動の加速について・・

zoro さんのレス (2007/08/02(Thu) 00:26)

＞肩甲骨はほかの骨に直接は接続していません．腕は鎖骨を通じて，背骨から生えています．

またユニークな解釈ですね．でも，次のご説明は素晴らしいと感じます；

＞しかし，腕の長さを鎖骨も含めてイメージすると，その分長く使えて色々得です．

肩のヨーイング運動と考えられます．クロールや背泳ぎで，重要だとおもいます．同様なことが，腰の骨でも起こります．従って，胴体部が平行四辺形のような動きを起こします．

＃似た事が，平泳ぎやバタフライでも起きるのですが，左右が対象の運動の為に，大きなヨーイングが出来ないので，あえて言えば，左右別々な小さなヨーイングしかできないので，肩関節や肩甲骨の柔軟性が少ない中高年には難しい動きになります．

なお，肩周辺は，骨，腱，筋肉が複雑に交錯しているので，簡単に書きすぎました．運動に興味があれば，下記の本は面白いです．

肉単(ニクタン)〜語源から覚える解剖学英単語集〜 原島 広至・文とイラスト エヌ・ティー・エス，2004-12，東京都文京区

Re: 円運動の加速について・・

ｙama さんのレス (2007/08/02(Thu) 13:18)

飲み過ぎさんの計算には誤りがあり，正しくは次のようになると思います．

（角運動量）＝(∫(M/L)・x^2dx)・ω（←積分は，0〜L） ＝(1/3)・M・L^2・ω

従って，角運動量が保存されるならば，Lが変化すると V=Lω も変化します．

Re: 円運動の加速について・・

飲みすぎ さんのレス (2007/08/03(Fri) 14:16)

＞＞zoroさん，Johさん，yamaさん

色々とご教示，ご指摘ありがとうございます．m(__)m

自分もテニスで試行錯誤を繰返す度に， 腕や背中の骨や筋肉についてよく調べます． 背中の筋肉群は複雑ですが身近な話だけに面白いですね．

テニスでは， 胸骨→鎖骨→肩甲骨→背中の筋肉群→背骨という繋がりで 肩甲骨や腕を体に固定することができたり，大きな背中の力を 利用可能になったりします．

ご教示頂いた書籍類は図書館等にて探してみようと思っています． ありがとうございました．

>（角運動量）＝(∫(M/L)・x^2dx)・ω（←積分は，0〜L） >＝(1/3)・M・L^2・ω > >従って，角運動量が保存されるならば，Lが変化すると V=Lω も変化します．

ご指摘，ありがとうございます．(^^;)〉 この件について「質点」ではなく「剛体」という形で 考察を色々と試みているのですが，未だよく分かりません・・・・．

M（剛体の重さ）

←V（先端の速度） ｜ ｜L（剛体の長さ） ｜ ｜ω（角速度） ・（回転の中心）

この角運動量が，(1/3)・M・L^2・ωとして， この剛体の先端に物体が衝突して，剛体が停止した時， 剛体が物体に与えた運動量（力積？）をＰとすると，

P・L＝(1/3)・M・L^2・ω ↓ P＝(1/3)・M・L・ω＝(1/3)・M・V

よって， まとめますと， ●剛体が回転する時，剛体の長さＬが短いほど， 回転の先端の速度Ｖが大きくなる． ●その剛体の先端に物体が衝突する時， 剛体の回転の先端の速度Ｖが大きいほど， 物体に与える運動量（力積？）は大きい．

（つまり，コンパクトにスイングした方が ボールの飛距離は延びる．）

・・・となりそうなのですが， コンパクトなスイングで飛距離が出るなどという話は 聞いたこともなく，どうも納得がいきません． 何か大切なことを見逃しているような気がして・・．

どこか間違いがありましたら是非ご指摘頂きたく 重ね重ねではありますが，宜しくお願い致します．

Re: 円運動の加速について・・

ｙama さんのレス (2007/08/03(Fri) 17:09)

>●剛体が回転する時，剛体の長さＬが短いほど， 回転の先端の速度Ｖが大きくなる．

これは角運動量が一定であることを前提としています． この前提が成り立たない場合はこの限りではありません．

Re: 円運動の加速について・・

zoro さんのレス (2007/08/03(Fri) 19:30)

飲みすぎさん，ご質問をようやく理解出来ました．

普通の打撃の問題ではなくて，何か「ハンマー投げ」見たいな手法を取り入れたいというように感じたので，ちょっと説明を躊躇してしまいました．

さて，お書きの下図で，回転中心は，体軸〜脊柱を表し，剛体の長さL〜「体軸，肩関節，腕，手，バットの打撃点」を表しているとします．取り合えずは，Lはお書きの通り，剛体と近似する訳ですね．

図１打撃体の仮定

M（剛体の重さ）

←V（先端の速度）＝ωL ｜ ｜L（剛体の長さ） ｜ ｜ω（角速度） ・（回転の中心）

そうすると，当面の問題は，上記の打撃体に，左から質量mのボールが，速度vで右に飛んで来て，図1の位置で，バット先端に衝突すると，どのようにボールは跳ね返されるのか，と言う事が知りたいのでしょうか？

こんな感じで良ければ，すこし考えて見ますが？でも，弾性衝突とすると，あまり面白い解ではないようにも感じます．衝突によって，打撃系に何かの条件を課すと良いのかも知れませんね．

大雑把にいえば，ボールとバットは衝突の前後で力積(FΔt)を交換して，ボールは反射して飛び出し，バットは力積を逆向きのトルクとして受けて角運動量を減少する，という計算になるように感じます．ヒョットして，どこかの演習問題にないでしょうかね(笑)．

他の事をしていて検討出来ませんでしたが，簡単に速度Vで走る平面に速度vで衝突すると，直感的に（v＋V）で反射すると思っていたのですが，違う様で，逆向きにvで戻るだけのようです．

確かに，加速するにはバットから，ボールに力積をあたえる必要があります．それは，角運動量の時事変化がトルクになる事をもちいます．取り敢えず，式だけを書いて置きます．

打撃体の角運動量の時間変化

I\frac{\mbox{d}\omega}{\mbox{d}t}=LF(t) \tag{1}

ボールの運動量の時間変化:打撃体との作用反作用を考慮して，

m\frac{\mbox{d} v}{\mbox{d}t}=-F(t) \tag{2}

こうすると，衝突の最中に発生する相互作用 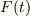F(t) をある時間幅に，一定の値で発生すると仮定すると，ボールの速度変化は式(2)で求められて，他方，その打撃力Fは，式(1)の作り出す体の筋肉トルク，関節の剛性などの解析から検討する事が出来るのだと思います．

これを得るには，ボールの速度，打撃のストローク映像，打撃の初速度，できれば打撃の高速撮影(ボールがバットに接触している時間幅，其のときのバットなどの姿勢変化)などがあれば，面白い解析になりそうです．おそらく，米国人の事ですから，上記のような解析をやっているのではないかと思いますが如何なものでしょうか．

でも，少なくとも，ボールとバットが接触している時に，打撃体(体軸からバットの先まで)が一丸となって，剛性を高め(関節を駆動する主動筋と対抗筋が同時に収縮し)すると共に，足の裏が地面をしっかりとホールドした上で，衝突の寸前にバット先に大きな 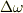\Delta \omega を作り出す為の筋トルクを足下から肩までに伝搬するような現象が起こっているのでしょうね．

是非とも，打撃のシンプル・モデルを構築して下さると嬉しいです．

クロールは足の裏が地面でないのですが，ある意味，トルクの伝搬としては野球の場合とも似た所があります．私は，トルク伝搬モデルのクロールの解析をしてみたいものです．

Re: 円運動の加速について・・

zoro さんのレス (2007/08/05(Sun) 18:18)

私は，最近でこそ水泳にハマっていますが，若い頃は，運動に興味がありませんでした．テニスのラケットの一部しか打撃に効果的でない事を始めて知ったくらいです．

すこしラケットとボールの相互作用を考える為に，寄り道をしてみたいと思います．

●〜〜〜〜〜〜〜〜〜〜〜〜〜〜● ボールと板（ラケット系）との衝突 ●〜〜〜〜〜〜〜〜〜〜〜〜〜〜●

図１ボールと板(ラケット系)との衝突 <pre> a) 衝突の前＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 板：質量M ボール：質量m┏┓ ● ┃┃

┗┛

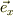
ーーー→速さv速さV←ーーーーー \vec v = v\vec e_x \vec V = -V\vec e_x

↑

静止座標原点:O------→ \vec e_x

b）衝突の直前／直後 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ ┏┓ ●┃┃ ┗┛

↑

重心点：G 重心の速さ：VG=(mv-MV)/(m+M) は衝突の前後でも保存する．

c）衝突の後＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ ┏┓ ●┃┃ ┗┛

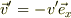
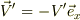
←ーーーーーーー速さv'←ー速さV' \vec v' = -v'\vec e_x \vec V' = -V'\vec e_x

〜〜〜

念のために必要な式の関係を書いて置きます．面倒なら結果，式(6a,b)以降だけを見て下さい．なお，検算はしていないので，議注意下さい．

重心速度と相対速度(板からボールを見た)；

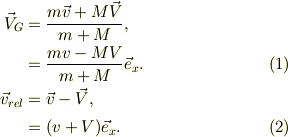
\vec V_G &= \frac{m\vec v +M\vec V}{m+M},\\&= \frac{mv -MV}{m+M}\vec e_x. \tag{1}\\\vec v_{rel} &= \vec v - \vec V,\\&= (v+V)\vec e_x. \tag{2}

衝突後には，式(2)の大きさが反転して，反発係数， e 倍になるから，

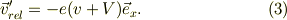
\vec v'_{rel} = -e(v+V)\vec e_x. \tag{3}

従って，衝突後のボールの速度は，重心Gが相対速度を「M:m」内分するので，

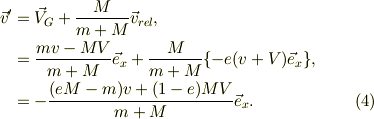
\vec v'&= \vec V_G + \frac{M}{m+M}\vec v_{rel},\\&= \frac{mv -MV}{m+M}\vec e_x +\frac{M}{m+M}\{ -e(v+V)\vec e_x \},\\&= -\frac{(eM-m)v +(1-e)MV}{m+M}\vec e_x. \tag{4}

同様に，衝突後の板の速度は，

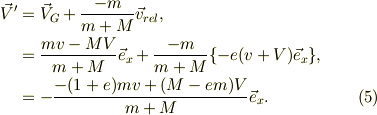
\vec V'&= \vec V_G + \frac{-m}{m+M}\vec v_{rel},\\&= \frac{mv -MV}{m+M}\vec e_x +\frac{-m}{m+M}\{ -e(v+V)\vec e_x \},\\&= -\frac{-(1+e)mv +(M-em)V}{m+M}\vec e_x. \tag{5}

衝突後の速さは，

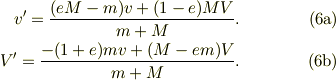
v'= \frac{(eM-m)v +(1-e)MV}{m+M}. \tag{6a}\\V'= \frac{-(1+e)mv +(M-em)V}{m+M}. \tag{6b}

たとえば，ラケットを振らないで静止して(V=0)いるところに，ボールに当てて，ボールが跳ね返る場合を，VTRで撮影し，(v, v')を測定すれば，ラケットと人体系の見かけの質量が判りますね．

なお，衝突係数， e は，水平に固定したラケットに一定の位置からボールを落下させた時の，反跳高さから実験的に求められますね．

Re: 円運動の加速について・・

飲みすぎ さんのレス (2007/08/06(Mon) 02:41)

＞＞zoroさん

色々とご教示いただき，ありがとうございます．m(__)m

重心速度というのは個人的に聞き慣れない言葉なのですが ボールと板を一つの物体として考えた場合の重心の速度は 衝突前後で保存されると解釈すれば良いのでしょうか． （間違ってるかな．．）

先の剛体の回転中心は，テニスで言えば「踏込み足」なのですが， 踏込んだ後，体の重心位置が回転するので，運動量保存則，角運動量保存則を どの様に駆使すれば全体の動きを把握できるのか・・・というのが現在の自分の ハードルです．気長に考えてみるつもりです．

ところで，ボールと板との衝突についてですが， 自分としては以下の認識なのですが，如何でしょうか． ━━━━━━━━━━━━━━━━━━━━━ m・(-v)＋M・V＝m・v'＋M・V' V'−v'＝−e・(V−(−v)) ↓ m≪Mの時， v'＝V＋e・(v＋V)（0≦ｅ≦１） ━━━━━━━━━━━━━━━━━━━━━

−−−−− >是非とも，打撃のシンプル・モデルを構築して下さると嬉しいです．

難しいですが，今後がんばって構築していきいたいと思っています．

テニスは複雑そうで意外とシンプル・・と言いますか， 考えをシンプルにしないと逆に使えないので，体を剛体と考えた部分は ちゃんと剛体になる様にしてやらないと問題になってしまったりします．

（その辺りテニスはシビアで，動き回るスポーツなくせに，ラケットとボール との接触時間は約0.004秒などと言われていますので，如何に無理なく 体を剛体化するのかという部分は，テニスを上手くなる為の秘訣でもあります．）

因みに， 「体の脱力と剛体化」を同時に満足させる方法として， 「絞った雑巾は硬くなる」という方法があります． 個人的にスポーツ全般に対して非常に有効な方法ではないか と思っています．

Re: 円運動の加速について・・

zoro さんのレス (2007/08/06(Mon) 10:20)

＞ボールと板を一つの物体として考えた場合の重心の速度は ＞衝突前後で保存されると解釈すれば良いのでしょうか．

接触している場合を「一つの物体」と言えるとは思います．でも，ニュートンの運動方程式で，大切なのは，外力の無い系，今の場合でしたら，ボールと板は離れている場合も含んで，系全体の運動量の保存がされます．

例えば，衝突前の系全体の運動量は；

\vec P \equiv m\vec v + M\vec V, \tag{7}

ですが，此れを辺々，系全体の全質量， (m+M) で割ると，

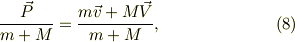
\frac{\vec P}{m+M}=\frac{m\vec v + M\vec V}{m+M}, \tag{8}

となります．これを式(1)と比較すると同じですね．

このように，外から力を受けない系では，その重心は，何が何でも一定，逆に言えば，等速運動する系，いわゆる慣性系となります．力学運動を考える時に，慣性系が判っていると，とても重宝します．ですから，今回も，重心の速度を先に持ってきました．

他方，今回は運動方程式からの説明を端折りましたが，系の相互作用する力を表すのには，相対座標が便利です．とくに，今回はボールがラケットに垂直に入射する場合を考えましたが，将来に，斜め入射してスピンを掛ける様な論議にも容易に拡張出来るように仕組んでみました．ここら辺は，一度，質点系の力学を勉強すると良いかも知れません．

＞先の剛体の回転中心は，テニスで言えば「踏込み足」なのですが， ＞踏込んだ後，体の重心位置が回転するので，運動量保存則，角運動量保存則を ＞どの様に駆使すれば全体の動きを把握できるのか・・・というのが現在の自分の ＞ハードルです．気長に考えてみるつもりです．

明快な視点だと思いますので，粗い近似からモデル計算したいですね．たしかにテニスというか，対戦形の競技では，自分から動いて行って，対抗運動をするのですよね．水泳では，ジャンプとかターン以外では，自分で思うように自分を操作するだけなのですよね．ここが両者の違う所である事を理解出来ました．

私は，テニスはやった事がありませんが，「テニスの王子様」というアニメは時々みます．腰を中腰として，左右前後に飛び出せるように構え，最良点に移動して，打つ為にラケットを逆回転してから，ストロークを開始するように見えます．

腕の伸びる方向こそちがえ，クロールの腕ストロークの運動はとても類似の現象と思います．

＞テニスは複雑そうで意外とシンプル・・と言いますか， ＞考えをシンプルにしないと逆に使えないので，体を剛体と考えた部分は ＞ちゃんと剛体になる様にしてやらないと問題になってしまったりします．

水泳でも，脚ビートによって作られた前方推進力を胴体部分で減衰する事無く肩から腕に推進力を伝達させる事が重要と思います．クロールでは胴体が捩じれることで剛性が高まると感じています．すると，平泳ぎやバタフライではどのように剛性を上げるのか，といった疑問が出てくる訳です．

陸の上の競技では，嫌でも重力による地面への押しつけがあるので，此れを有効利用すると考えるのも面白そうです．でも，力学モデルが大変ですが，最近はコンピュタ上のお猿さんが水平の梯子を，ブランブランと渡る様なご時世ですから，ヒトがテニスするシミュレートとあながち不可能ではないかも知れませんね．

＞（その辺りテニスはシビアで，動き回るスポーツなくせに，ラケットとボール ＞との接触時間は約0.004秒などと言われていますので，如何に無理なく ＞体を剛体化するのかという部分は，テニスを上手くなる為の秘訣でもあります．）

こんなに短い訳ですか．やはり空気中の運動だからでしょうね．ちなみに，ラケットやボールの質量はどれくらいでしょうか？

＞「体の脱力と剛体化」を同時に満足させる方法として， ＞「絞った雑巾は硬くなる」という方法があります． ＞個人的にスポーツ全般に対して非常に有効な方法ではないか ＞と思っています．

水泳では； ・推進力を出す場合，腕や脚の内旋運動がメインで， ・腕を前に戻すリカバリでは，肩甲骨の内転と上腕の外旋がメイン， となるようです．

＞ところで，ボールと板との衝突についてですが， ＞自分としては以下の認識なのですが，如何でしょうか．

このところ，夏バテぎみで，考えが定まりにくいので，すこし宿題にさせて下さい．