回転座標系における慣性力
回転座標系における慣性力
eKinetic さんの書込 (2007/07/27(Fri) 17:50)
慣性系に対して,加速度 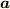 で運動している非慣性系上にいる観測者が,質量
で運動している非慣性系上にいる観測者が,質量  の物体を見ると,
の物体を見ると,
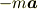
という,慣性力が働いているように見えます.この慣性力の中の, 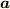 は,観測者自身の加速度
は,観測者自身の加速度 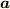 であると理解しています.
であると理解しています.
一方,角速度  の回転座標系上にいる観測者が,半径
の回転座標系上にいる観測者が,半径  の位置にある質量
の位置にある質量  の物体を見ると,
の物体を見ると,
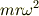
の大きさの慣性力(遠心力)が,外向きに働いているように見えますが,これは,観測者の位置(半径)によらず,同じ値であると思います.
つまり,観測者の加速度は,観測者のいる位置の半径によって異なるはずなのに,質量  の物体に働く慣性力は,その物体の位置の半径
の物体に働く慣性力は,その物体の位置の半径  によって決定されてしまいます.
によって決定されてしまいます.
このことは,回転座標系上で慣性力を考える場合,慣性系から見た物体の加速度が本質的であって,観測者自身の加速度は関係がない,ということなのでしょうか.
Re: 回転座標系における慣性力
eKinetic さんのレス (2007/07/27(Fri) 22:10)
>>これは,観測者の位置(半径)によらず,同じ値であると思います.
>これは正しいんでしょうか.
円盤の中心にばねを取り付け,一方に物体を付けて回転させる場合,回転座標系では,物体に働くばねの弾性力と遠心力とがつり合っていると考えます. このとき,観測者が円盤上のどこにいても,ばねの伸びは同じに見えるはずで,それは,観測者の位置にかかわらず,物体に働く遠心力は同じであるということだと思います.
Re: 回転座標系における慣性力
toorisugari no Hiro さんのレス (2007/07/28(Sat) 01:44)
おおむね eKinetic さんの考察で正しいと思います.
線形な座標変換(変位ベクトルと変換された変位ベクトルの間に線形関係が成り立つ)は
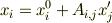
で表されます.(ポアンカレ変換)
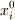 は原点の並進移動,すなわち,観測者の位置の変更と考えられます.
は原点の並進移動,すなわち,観測者の位置の変更と考えられます.
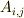 は座標軸の向きやスケールの変更(通常は直交変換を考えるので座標軸の回転),すなわち,観測者の向いている方角の変更と考えられます.
は座標軸の向きやスケールの変更(通常は直交変換を考えるので座標軸の回転),すなわち,観測者の向いている方角の変更と考えられます.
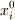 も
も 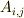 も(
も( 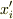 には依存しませんが)時間に依存します.もし,ふたつとも定数なら空間の並進対称性,回転対称性によりどちらの座標も平等,つまり,物理法則は同等です.
には依存しませんが)時間に依存します.もし,ふたつとも定数なら空間の並進対称性,回転対称性によりどちらの座標も平等,つまり,物理法則は同等です.
慣性力とは本来,上の式を時間で2階微分した
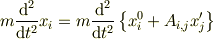
と, 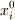 も
も 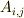 も定数として計算した
も定数として計算した
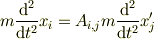
との差に当たるもので, 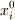 と
と 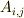 の時間依存性による付加項が慣性力です.
の時間依存性による付加項が慣性力です.
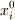 が足し算的な変化,
が足し算的な変化, 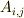 がかけ算的な変化です.足し算的な変化のときのみ,物体に「作用」する慣性力は観測者の加速度で表されると解釈できます.一般には観測者の加速度だけでなく物体の(観測者からみた)相対位置
がかけ算的な変化です.足し算的な変化のときのみ,物体に「作用」する慣性力は観測者の加速度で表されると解釈できます.一般には観測者の加速度だけでなく物体の(観測者からみた)相対位置 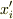 や相対速度
や相対速度 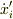 にも依存します(
にも依存します( 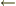 積の微分則).
積の微分則).
# なお, 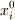 が時間の線形関数の場合,慣性項が現れません.これが慣性座標系の対称性(ガリレイ不変性)になります.
が時間の線形関数の場合,慣性項が現れません.これが慣性座標系の対称性(ガリレイ不変性)になります.
Re: 回転座標系における慣性力
zoro さんのレス (2007/07/28(Sat) 07:51)
eKineticさん,
面白い切り口の考え方だと思います.寝苦しい夜だったので,寝ながら考えて見ました.
気になるのは,回転系の座標原点にバネの一端を止める場合,ピンによる固定(位置は固定するが,回転のトルクは発生しない)では駄目で,回転も固定する必要があることと,原理的にもバネとおもりは有限の長さを持つ必要があります.
一方,回転系の座標原点から有限距離だけ離れた点では,ピンによる固定だけで,バネは一意的に伸びると思います.
いずれにしろ,「eKinetic式バネ」の論法で,遠心力の分析を出してみると,素晴らしいと思います.
Re: 回転座標系における慣性力
eKinetic さんのレス (2007/07/28(Sat) 18:51)
>toorisugari no Hiro さん
ありがとうございます.
慣性系 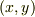 に対し,回転座標系
に対し,回転座標系 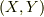 の原点の並進移動はないとして,
の原点の並進移動はないとして,
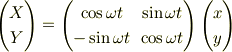
これを,2階微分して,
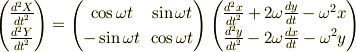
を得ました.
右辺の行列の部分が, 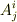 それ以外が,
それ以外が, 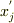 に相当するということで,あってますか?
に相当するということで,あってますか?
>物体の相対位置や相対速度にも依存します
相対位置とは, 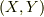 のことで,
のことで,
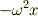
の項にあたる部分,
相対速度とは, 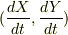 のことであって,
のことであって,
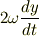
の項にあたる部分である,
ということで,よいのでしょうか?
>zoro さん
コメントありがとうございます. やさしい口調に,勇気づけられます.
Re: 回転座標系における慣性力
toorisugari no Hiro さんのレス (2007/07/29(Sun) 14:07)
>相対位置とは, 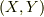 のことで,
>
のことで,
>
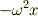
>の項にあたる部分,
>相対速度とは, 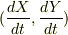 のことであって,
>
のことであって,
>
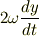
>の項にあたる部分である, >ということで,よいのでしょうか?
はい.慣性力としてみたとき前者が遠心力,後者がコリオリ力に相当します.
Re: 回転座標系における慣性力
eKinetic さんのレス (2007/07/31(Tue) 17:24)
お礼が遅れて,申し訳ありません.
2階微分
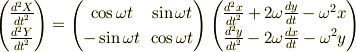
の右辺を, 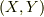 で表せばもっとよくなると思い,ようやく,
で表せばもっとよくなると思い,ようやく,
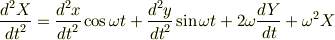
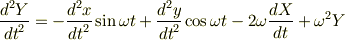
にたどり着きました.ここで,
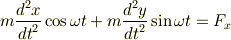
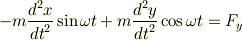
とおいて,運動方程式が次のようになりました.
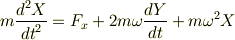
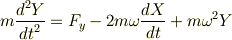
右辺第2項が,>コリオリ力,第3項が,>遠心力ということだと思います.
間違いがありましたらご指摘ください. 私は成分に分けて計算ミスばかりしましたが,おそらくベクトルのまま演算するやり方もあるのだと思います. 今後の勉強の課題にします.
長い間のもやもやが,かなりすっきりしました.
toorisugari no Hiro さん,zoro さん ありがとうございました.
Re: 回転座標系における慣性力
zoro さんのレス (2007/07/31(Tue) 17:56)
>右辺を,(X,Y)で表せばもっとよくなると思い
これはとても自然な解釈だとおもいます.これを一人で成し遂げた所が凄いとおもいます.
そもそも,お書きになった最初の式,
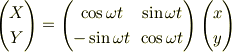
を逆に解いて,というよりは,(X,Y)系から(x,y)を見ると,角度が逆に見える筈なので,
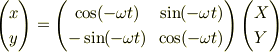
としてしまうと,式操作は楽になります.
なお,重要な事は,運動方程式を立てられるのは,あくまで慣性系 (x,y) であります.回転系のような非慣性系では,常に,回転座標自身の時間微分が出てきて,それゆえの項目が出てくるわけですよね.
これからも,非慣性系の問題を見たときには,常に慣性系から立式して,非慣性系の式に移ると感じられると間違えないですね.
〜〜〜 でも,今回お示しになった計算により,とても見通しが良くなったと思うので,次の課題に挑戦して下さい.
例えば,2次元であれば,行列法も有力ですが,複素数表示も結構,軽快です.
勿論,3次元であれば,行列法はとてもパワフルですよね.でも,そこまで来ると,テンソル形式や,外微分形式などもあるようですが,私もこれらか勉強しようかと思っています.
〜〜〜 アイデアは豊富に,でも裏づけは丁寧に!
Re: 回転座標系における慣性力
eKinetic さんのレス (2007/08/01(Wed) 11:31)
>(X,Y)系から(x,y)を見ると >式操作は楽になります
やってみました.
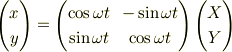
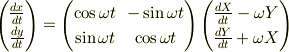
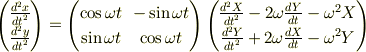
ありがとうございました.>zoroさん.
話題とずれてしまいますが... 私は成分に分けて計算し,行列は,結果を見やすくまとめるのに使っただけです. このとき,位置,速度,加速度すべてに,なぜ同じ行列が出てきたのか,わかりません. 行列操作の学習をすれば,わかるでしょうか?
今回,Johさんにもコメントをいただき,感謝申し上げます.
Re: 回転座標系における慣性力
ミュフ猫 さんのレス (2007/08/01(Wed) 13:48)
>位置,速度,加速度すべてに,なぜ同じ行列が出てきたのか,わかりません.
空間の等方性により,これらのベクトル量の空間分布(つまり,ベクトル場)が 軸に対して回転対称になるからかな?
Re: 回転座標系における慣性力
zoro さんのレス (2007/08/01(Wed) 18:30)
>>位置,速度,加速度すべてに,なぜ同じ行列が出てきたのか,わかりません.
私は検算していませんでした.eKineticさんの計算力を信じていました.そこで,自分なりに得意の複素数をつかった算術を少しだけしてみます.
其の為に,座標の取り方を確認します.
<pre> i | P
y・−−−−−−−−−・e^(iωt)
|// / |/ /| / |// |/ |/ /| / |// |・X |/ / |/ |/ / |/ |/ /| / |// |/ / / / /|/ /| ie^(iωt) /| / /| /|/ /| /| / /| Y ・| / /| | / /| |/ /| | //| |/| ・−−−−−−−−−・−−−−−−−−−1 O x
●Oxyは慣性座標系 ●OXYは回転座標系:Oxyに対して一定の角速度ωでCCW方向に回転. ∠XOx = ωt </pre>
多分皆さんは,ヴェクタ表示と複素数表示との併用に慣れていないと思いますので,パラに書いて行きます.質点Pの位置を,Oxyでみれば,

同様に,OXYで見れば,
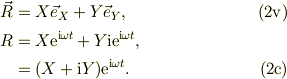
式(1c)(2c)はP点の位置複素数を表しているから,
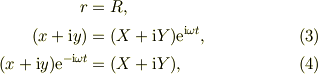
と,幾らでも好きな関係を出せますね.
今回の場合,式(3)を元にして,辺々を時間で適宜に微分すれば良いですね.
一応,例題として,速度を出して見ましょう.式(3)の時間微分ですから,
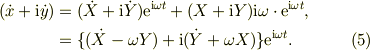
式(3),(5)を,ご自分で算出された行列形式と比較すると,対応関係が見えてきませんか?複素数形式の善いのは,回転行列の替わりに,オイラの公式が1つ出るだけなので,微分関係が簡単ですね.
最後の最後に,実部・虚部の切り分けが必要ですが...(笑). 〜〜〜 変数の取り方
今回の計算では「慣性系x,y」,「加速系 X,Y」とされていると思います.実際の計算では,外力の導入時に(x,y)を使うものの,以後は,(X,Y)が頻繁に使われます.
私だったら,計算式の書き易さから,「慣性系X,Y」,「加速系 x,y」とするかも知れません.
Re: 回転座標系における慣性力
toorisugari no Hiro さんのレス (2007/08/01(Wed) 18:30)
> このとき,位置,速度,加速度すべてに,なぜ同じ行列が出てきたのか,わかりません.
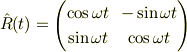
としたとき
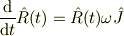
となる 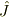 が比較的簡単な形の行列
が比較的簡単な形の行列
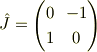
になるからです.(この行列は虚数単位とおなじ代数的性質を持っています.これを生かせば,zoroさんのおっしゃるとおり,2次元ベクトルでなく複素数で計算できます.)
Re: 回転座標系における慣性力
eKinetic さんのレス (2007/08/01(Wed) 21:57)
ミュフ猫 さん,zoro さん,toorisugari no Hiro さん ありがとうございました.
きちんと理解するには,時間がかかりそうですが,すごく勉強になっています. わからないことを聞ける幸せを感じます. 今回の件以外にも,わからないことが山ほどあり,またお世話になると思いますので,どうぞよろしくお願いいたします.
ただ,こうして時間をさいて教えてくださる方に,何もお返しできないのが残念です.
以上,簡単ですが,お礼まで.
Re: 回転座標系における慣性力
zoro さんのレス (2007/08/01(Wed) 22:28)
>ただ,こうして時間をさいて教えてくださる方に,何もお返しできないのが残念です.
恐らく,このスレッドに書き込まれた方々は,eKineticさんの問題提起,数式の処理などに共感されたので,「それに対して説明をしよう」とされたのだと推測します.
何時の日にか,「eKineticさんが逆に教える側に廻る」ことを希望しますね.