フーリエ級数
フーリエ級数
けん(大学2年) さんの書込 (2007/07/27(Fri) 12:04)
フーリエコサイン級数の問題です.
f(x)=1 を[0,L]でフーリエコサイン級数展開するとコサインは現れず, f(x)=1 となります. フーリエサイン級数展開ではサイン関数で表されるのにフーリエコサイン級数展開ではコサインが消えるのは,f(x)=1という関数からあらかじめ予想できることなのでしょうか?よろしくお願いします.
Re: フーリエ級数
toorisugari no Hiro さんのレス (2007/07/27(Fri) 12:54)
周期は  ですか,
ですか, 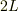 ですか?
ですか?
Re: フーリエ級数
けん(大学2年) さんのレス (2007/08/02(Thu) 18:34)
周期2Lで級数展開しました.
Re: フーリエ級数
けん(大学2年) さんのレス (2007/08/03(Fri) 14:28)
偶関数として[-L,L]に関数を拡張し,周期2Lで展開しました. 説明不足ですみません.
Re: フーリエ級数
toorisugari no Hiro さんのレス (2007/08/03(Fri) 15:22)
> 偶関数として[-L,L]に関数を拡張し,周期2Lで展開しました.
ではサインで展開した結果は常に0になりませんか?
Re: フーリエ級数
けん(大学2年) さんのレス (2007/08/06(Mon) 13:39)
サインの場合はもちろん奇関数として拡張しました.
Re: フーリエ級数
toorisugari no Hiro さんのレス (2007/08/06(Mon) 20:31)
> 偶関数として[-L,L]に関数を拡張し,周期2Lで展開しました. > サインの場合はもちろん奇関数として拡張しました.
「もちろん」ですまさないでください.これを最初に言ってください.
> f(x)=1 > を[0,L]でフーリエコサイン級数展開するとコサインは現れず, > f(x)=1 > となります. > フーリエサイン級数展開ではサイン関数で表されるのにフーリエコサイン級数展開ではコサインが消えるのは,f(x)=1という関数からあらかじめ予想できることなのでしょうか?
式できちんと表現して,前提を正しく書いてもらわないと,何をおっしゃっているのか理解できません.
たぶん, 「
![f(x)=1 \qquad x\in[0,L]](http://hooktail.maxwell.jp/bbslog/a8c9e2126f241af5d53d3142f540a816.png)
を偶関数(の周期関数)として[-L,L]に関数を拡張し,周期 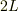 のコサイン関数群で展開したフーリエ係数は波数0の時のみ非零なのにたいして,
おなじものを『奇関数(の周期関数)として[-L,L]に関数を拡張』し,周期
のコサイン関数群で展開したフーリエ係数は波数0の時のみ非零なのにたいして,
おなじものを『奇関数(の周期関数)として[-L,L]に関数を拡張』し,周期 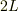 のサイン関数群で展開したフーリエ係数はすべてで非零なのはなぜか?
」
という問いでしょうね?(とても最初の質問ではわかりません.)
のサイン関数群で展開したフーリエ係数はすべてで非零なのはなぜか?
」
という問いでしょうね?(とても最初の質問ではわかりません.)
答えは後者の拡張された関数に不連続点があるからです.
「f(x)=1という関数からあらかじめ予想」できません.「奇関数と」(不連続を含むように)拡張したからです. # そもそも関数が違うのですから.
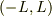 or
or 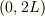 でなく,
でなく, 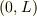 ですか?
ですか?