少数キャリア連続の式
少数キャリア連続の式
tip★ さんの書込 (2007/07/23(Mon) 23:03)
(問題)p形半導体に光を照射して伝導電子を生成させる時,単位時間当たりg個/ 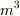 の電子・正孔対が作られ,電子の寿命が
の電子・正孔対が作られ,電子の寿命が 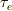 であるとして,光照射後の電子濃度を求めよ.ただし,電流は流れないものとする.
であるとして,光照射後の電子濃度を求めよ.ただし,電流は流れないものとする.
(解)
少数キャリア連続の式に光照射の効果を加えると,
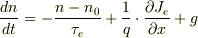 で,
で, 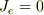 なので,
なので,
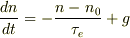 となる.
となる.
この後,どうやって解いていけばいいのか検討がつきません.どなたかアドバイスお願いします.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/23(Mon) 23:36)
仰られている方程式の意味を理解していませんが,最後の式;
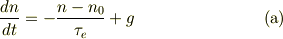
で,nが時間だけの関数で,他のn_{0},tau_{e},gが常数なら,

と置くと,簡単になる様な気がしますが.
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/24(Tue) 00:09)
は何のことを示すのでしょうか?
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/24(Tue) 00:32)
微分方程式(a)の物理的な意味が判らないので,現段階では解釈は出来ません.
ただ式(b)を式(a)に代入すると;
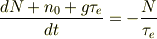
もし,左辺の「 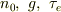 」が定数なら,
」が定数なら,

となり,積分出来ますよね.それには初期条件が必要ですが....
解けてしまえば,Nは式(b)によりnに戻せば善いので,Nの意味は知らなくてもいいとも考えられます.
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/24(Tue) 00:58)
多分ですが,初期条件が与えられていないので,微分方程式を解く問題ではないか,または,自分で初期条件を探さなければいけないと思うのですが.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/24(Tue) 02:27)
式(c)を変数分離形に出来る;
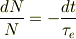
ので,辺々を積分して;
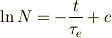
いま,t=0の時, 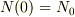 とすれば,積分常数は
とすれば,積分常数は 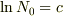 だから,
だから,
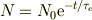
これを式(b)に戻せば,
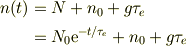
ここで,t=0での値に注目すると;
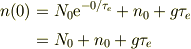
故に
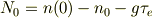
この式でN_0 を消去できるから,
![n(t) &= [n(0) -n_0 -g\tau_{e}]\mbox{e}^{-t/\tau_e } +n_0 +g\tau_{e}\\&= n(0)\mbox{e}^{-t/\tau_e } +(n_0 +g\tau_{e})[1-\mbox{e}^{-t/\tau_e }] \tag{d}](http://hooktail.maxwell.jp/bbslog/dad4c323fa1853e70d602d772898061d.png)
式(d)の再終行の右辺第1項は,初期値,n(0)が単純に崩壊することを表します.
その右辺第二項の「n_0」の意味は不明です. 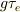 の部分は,光の連続照射が平均時間
の部分は,光の連続照射が平均時間 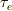 あって,崩壊しつつも蓄積する部分を表すと思います.
あって,崩壊しつつも蓄積する部分を表すと思います.
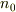 の意味は,元の方程式の段階で確認する必要がありますね.どうやら最初の「少数キャリア連続の式」にヒントがあるようですね?普通の減衰挙動と違って,
の意味は,元の方程式の段階で確認する必要がありますね.どうやら最初の「少数キャリア連続の式」にヒントがあるようですね?普通の減衰挙動と違って,  は
は 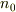 を境に,減衰も成長もする要です.この意味が知りたいと思います.その意味では,
を境に,減衰も成長もする要です.この意味が知りたいと思います.その意味では,
![n(t) &= n(0)\mbox{e}^{-t/\tau_e } +(n_0 +g\tau_{e})[1-\mbox{e}^{-t/\tau_e }] \\ &= n_0 +[n(0) -n_0 ] \mbox{e}^{-t/\tau_e } + g\tau_{e}[1-\mbox{e}^{-t/\tau_e }] \tag{e}](http://hooktail.maxwell.jp/bbslog/cc661d06ef2e49acd6f823e26e6e719f.png)
とすると,なんとなく感じが出ませんか?
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/24(Tue) 10:22)
は熱平衡状態の伝導電子濃度のことです.
式(d)をさらに変形して,
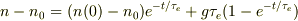 となり,右辺の第1項の部分は熱平衡状態時の値
となり,右辺の第1項の部分は熱平衡状態時の値 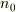 に対して余分な電子濃度が,
に対して余分な電子濃度が, 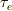 を時定数として指数関数的に減少することを表していると思います.
を時定数として指数関数的に減少することを表していると思います.
第2項は  の
の 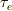 倍の伝導電子が増加していることを表しているように感じます.
倍の伝導電子が増加していることを表しているように感じます.
あとは,t→∞とすればいいような気がしますがどうでしょうか?
今から講義なので,聞いてきます.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/24(Tue) 11:00)
>あとは,t→∞とすればいいような気がしますがどうでしょうか?
という定常解が欲しい場合,式(a)の左辺をゼロ(定常解なので,変化率はゼロの筈だから)に置いてしまえば良いですよね.検算の一法にもなりますよ.
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/24(Tue) 11:47)
答え聞いてきました.
zoroさん,のおっしゃるとおり,
定常状態では, 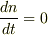 なので・・・
というのを使うみたいです.
なので・・・
というのを使うみたいです.
定常状態というのは,インプットとアウトプットがつりあっていて変化がない状態だと思っていたのですが,t→∞とした場合の状態のことを定常状態というのでしょうか?
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/24(Tue) 12:19)
追加質問です.
定常状態で元の微分方程式を解くと
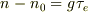
となります.
定常状態ではnの変化がない状態なので, 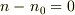 とならないと感覚的に矛盾している気がするのですが,解の物理的意味はどのように解釈すればいいでしょうか?
とならないと感覚的に矛盾している気がするのですが,解の物理的意味はどのように解釈すればいいでしょうか?
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/24(Tue) 14:16)
>定常状態ではnの変化がない状態なので,n-n_{0}=0とならないと感覚的に矛盾している気がする
仰っているのは,照射の無い時のある温度での電子・ホールの数みたいなものが 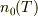 といったイメージで,t=0から光の照射が始まり,これによる電子・ホール対の発生,その再結合による減少が一定になるようにバランスしたようなものだと思います.
といったイメージで,t=0から光の照射が始まり,これによる電子・ホール対の発生,その再結合による減少が一定になるようにバランスしたようなものだと思います.
極限としては,以前の時間に光照射で生成した分を指数減少を考慮しながら足し合わせても,高々, 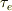 の時間幅の照射による電子(ないしホール)が
が実効的に
の時間幅の照射による電子(ないしホール)が
が実効的に 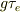 だけ生き残ると考えるのでは?
だけ生き残ると考えるのでは?
ご注意: 私は,半導体用語を不明瞭にしか理解していません.変な所をご教示下さると幸いです.
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/25(Wed) 01:02)
すいまんせん,ちょっとイメージがわきません.
自分がt→∞と書き込んだとき,なぜ定常状態だと解釈したのか理由はなんでしょうか?できれば,定常状態の定義から解説してほしいです.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/25(Wed) 05:12)
>すいまんせん,ちょっとイメージがわきません.
私も,理由こそ違え,完全に理解出来ていません.そこで,半導体の計算式を復習しています.
- http://www.aki.che.tohoku.ac.jp/~tonodera/fermi.pdf
- http://www.dt.takuma-ct.ac.jp/~tsuji/java/carrier_dens/carrier_dens.html
両者は一長一短ですが,式の操作過程は(2)が解り易いので此れを追っています.
#特に(2)の図が全滅なのが惜しまれます.
>自分がt→∞と書き込んだとき,なぜ定常状態だと解釈したのか理由はなんでしょうか?できれば,定常状態の定義から解説してほしいです.
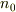 や,もともとの少数キャリア
や,もともとの少数キャリア  も含めて,それらの物理的な意味が判らないのが解りました.最初は,微分方程式の感じから,電荷密度の保存則の式を基に,幾つからの負荷項目が付いた式,位にしか考えていませんでした.従って,この式の本当の解釈は,現時点では無理です.
も含めて,それらの物理的な意味が判らないのが解りました.最初は,微分方程式の感じから,電荷密度の保存則の式を基に,幾つからの負荷項目が付いた式,位にしか考えていませんでした.従って,この式の本当の解釈は,現時点では無理です.
でも,基本的には,tip★さんが書かれた;
>定常状態というのは,インプットとアウトプットがつりあっていて変化がない状態だと思っていたのですが,t→∞とした場合の状態のことを定常状態というのでしょうか?
がいい点を突かれていると思います.例えば,空から降って来る「雨」は地上に達する時には一定速度で落ちてきますよね.電車の窓にあたる雨の流れを見ていれば,ほとんど平行な軌跡が見えますから.
この雨の垂直方向の運動方程式は,
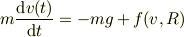
これを真っ向から解こうとすると大変に難しいのです.というのは摩擦力 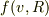 は,雨粒の半径
は,雨粒の半径  に依存した上で,速度
に依存した上で,速度 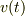 の関数でもあるからです.
の関数でもあるからです.
ところが,定常解だけは,「左辺がゼロに漸近する」と仮定するだけで求まってしまいます.あとは, 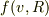 を色々換えてチェックすることに問題が転化します.この場合は,
・重力と摩擦力とがバランスしたので,
・加速度がゼロになり,
・速度が一定になった,
と考えても良い訳ですね.「典型的な定常」の事例と思われます.
を色々換えてチェックすることに問題が転化します.この場合は,
・重力と摩擦力とがバランスしたので,
・加速度がゼロになり,
・速度が一定になった,
と考えても良い訳ですね.「典型的な定常」の事例と思われます.
他方,「ほぼ定常状態」というのがあると思います.交流を半波整流する場合がそれです.t=0に電圧・電流が無い所から一定負荷にどのような電圧が掛かるかを出す訳ですね.どんな計算をしたか忘れていますが,印可サイクルが増えるに従って,ある値に漸近するも,一周期ごとの微小変化(リップル)が取りきれません.もちろん,一周期についての平均値は一定になります.
#似た様な現象が,水泳の場合にも起こります. #人間の「腕」や「脚」はどうしても,間欠的な推進力しか出せないからです. #特に平泳ぎでは脚の運行姿勢による抵抗が高いので,『極論する解析者は,一周期の間に「短時間ながら静止」する』とまで主張されているようです. #自分のモデルでも,リップルは取り除けないものの,静止するとは考えられませんでした.
ですから,今回の場合も, 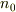 が,光子による励起過程に対向する消滅過程に対応すると考えたいのですが....そこで,半導体の計算の勉強に入っている所です.なにせ大昔に放棄したテーマなので,いつ判るか分りません,ポリポリ.
が,光子による励起過程に対向する消滅過程に対応すると考えたいのですが....そこで,半導体の計算の勉強に入っている所です.なにせ大昔に放棄したテーマなので,いつ判るか分りません,ポリポリ.
ですから,授業で質問して,回答をこちらに書き入れて下されば,嬉しいです.←攻守が交代していますね.
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/25(Wed) 13:07)
熱平衡状態は,電子の発生と再結合がつりあっている状態. 定常状態は,インプットとアウトプットがつり合っていて時間的変化がない状態.
調べたら,こういうのがのっていました.
でも,式(e)について,t→∞とすると,再結合を表す第2項は0となり,発生を表す第3項は 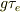 となり,再結合も発生も時間的変化がない状態となり,上に書いた定常状態と矛盾している気がします.
となり,再結合も発生も時間的変化がない状態となり,上に書いた定常状態と矛盾している気がします.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/25(Wed) 21:03)
先ほど,近くの区立の図書館で参考書を探したのですが,簡単な本しかなくて,今回の論議の光照射の微分方程式などを説明してありません.
もし,授業での推奨図書などがあれば,考えるトリガになるかも知れません.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/26(Thu) 10:13)
ネットで調べると,
というサイトが,pn接合の電流-電圧特性を求めようとしています.その中で式(7)が天下り的ですが与えられています.これは,前回書き込みました(2)のサイトと同じ筈ですが,相互の関係が良くわかりません.
従って,この前提を説明している様な半導体物理の本があれば良い筈です.
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/26(Thu) 11:14)
zoroさん,
教科書ではないのですが,上の問題が載っているテキストを先生から教えていただきました.
「新版基礎半導体工学」國岡昭夫・上村喜一著朝倉書店
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/26(Thu) 12:14)
tip★さん,
>上の問題が載っているテキストを先生から教えていただきました.
有り難うございます.近くの他の図書館も探してみます.
確かに,半導体物理は多角的な概念が集合して始まるので,理解するのが難しいですね.特に,定性的な理解と,それを裏付ける定量的な理解とをバランス良く進めるのが大事でしょうね.
今の調子で,色々解釈をして行くと,問題点が浮き上がると思います.
自分の場合,真性半導体のフェルミ準位がなぜバンドの中央に出て来るかを,熱力学的に講釈していただけたら,その後の理解がスムーズになると感じています.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/27(Fri) 01:14)
記法には未だ自信がありませんが,大枠としては判って来たように思います.
先ず簡単な為に真性半導体を考えます.原理的ですから外部との接続は無いとします.
当然,この半導体は,外部の温度T °K 一定として,熱平衡にあれば,
伝導帯出の電子数を  n,荷電帯でのホール数を
n,荷電帯でのホール数を 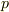 とすれば,電荷の中性条件から;
とすれば,電荷の中性条件から;

で熱平衡で,かつ定常状態にあります.この場合,「熱平衡」だから時間的に変動が無いのではありません.ミクロに系を観察できれば,時間的にも,運動の自由度kTのオーダのエネルギーをもらって電子・ホール対を作ったり,逆に電子・ホールが衝突して電子・ホール対が消滅することが頻繁に行われています.でもマクロに見れば,全体的には「n,p」は時間平均をとると平衡していて,定常状態に見える訳です.
ところが,ある時刻,t=0 から光を強度g一定で照射するとすれば,ある時刻の「n(t), p(t)」は n_iからずれて行きます.

こうすると,熱平衡の部分は 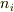 に押し付けておき,この部分は,上に述べたマクロの平衡にあると見なします.光照射による変化分が
に押し付けておき,この部分は,上に述べたマクロの平衡にあると見なします.光照射による変化分が 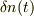 によって表せると考えられます.
によって表せると考えられます.
従って,ある時間に生じる変化は;
・光照射による一定の対の生成と,
・過剰な対の衝突による消滅による緩和過程「その寿命時間, 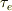 」とで,
生じるので,変化は次の微分方程式で表す事ができます;
」とで,
生じるので,変化は次の微分方程式で表す事ができます;
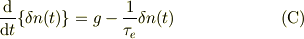
初期条件は, ![\delta n(t)]_{t=0} = 0](http://hooktail.maxwell.jp/bbslog/7f59145721f97e19caf33dadb4478050.png) です.
です.
上の式では,前者がインプット,後者がアウトプットと考えても良いでしょう.
式(C)の解を式(A)に代入すれば,欲しい濃度の時間変化となりますね.計算問題として解いて下さい.
〜〜〜 pn接合だ,外部から電位を印可する,負荷に電流を流すなどによって問題が複雑になりますが....それは,チップ★さんの,今後の課題になると思います.
Re: 少数キャリア連続の式
tip★ さんのレス (2007/07/27(Fri) 12:06)
zoroさん,
zoroさんにまかせっきりですみません.今ちょっとテスト期間中でなかなか時間が取れない状態にあります.テストが終わったら,もっと本格的に調べて理解を深めていきたいと考えています.
勝手ながら申し訳ありません.
Re: 少数キャリア連続の式
zoro さんのレス (2007/07/27(Fri) 12:33)
tip★さん,
>今ちょっとテスト期間中でなかなか時間が取れない状態にあります.テストが終わったら,もっと本格的に調べて理解を深めていきたいと考えています.
勿論,学校が最優先です.
テストで勉強していると,関連で興味が涌いて来て,そちらを調べてるうちに,テスト以外の理解が進んでしまったりしましたが....夏休みにじっくり考えて下さい.
>まかせっきりですみません.
こちらも好きでやっている事なので,お互い様です.この一連の論議を拝見していて,自分が若い頃に理解出来なかった点が幾つも出て来て,とても興味深く思いました.
そのうえ,趣味で検討している水泳の推進力の実験を考えているうちに,ダイオードとかトランジスタをつかった風力計を作れるのではないかと気づきました.半導体の知識が深まったので,とても面白いです.逆に,教えて戴く事がありそうですね.