半球
半球
bene さんの書込 (2007/07/22(Sun) 18:52)
はじめまして．わからない問題があります．過去ログにも同じ問題があったのですが，半球状のドームを物体が滑り落ちるときに，ドームと物体が離れる高さを求めよ．という問題です．過去ログを見てもうまく解決できませんでした． どうかやり方をお教えいただけませんでしょうか？
Re: 半球
ｋｏｍａｇａｔａｋｅ さんのレス (2007/07/22(Sun) 20:01)
どこで躓いたかがわかるといいのですが．
鉛直面内での振り子の円運動の問題はやられましたか．最下点での速度を与えて円運動をする条件とか水平から斜め上に４５℃のところで離れるとすると初速度はいくらかという問題です．少し変えて円筒の内面に沿って運動するというのもあります．円筒の外面に沿っての運動はドームの問題と同じですね．どれも考え方は共通です．
円運動の実現条件または接触条件は張力＞０，垂直抗力＞０です．円運動ですから向心力を考えます．高さの変化との速度の関係にはエネルギー保存を使います．
図を書いてもう一度やってみて下さい．いきなりドームでやらずに振り子の場合，から始めてみる方がいいでしょう． あちこちに問題が載っていると思います． やってみてこの部分がわからないという形で質問してもらうと答えやすいです．
Re: 半球
bene さんのレス (2007/07/23(Mon) 16:07)
重力による垂直抗力と向心力で釣り合いをだすんですよね？ それでうまくいかないんですが・・・ mgsinθ=mrω^2 であってますか？
Re: 半球
ｙama さんのレス (2007/07/23(Mon) 17:15)
θのとり方が分かりませんが，半球の中心と物体を結ぶ直線が水平方向となす角度であれば，その式で合っています． 右辺はωでなくて速さvを用いて表したほうがいいでしょう．
しかし，「重力による垂直抗力と向心力で釣り合いをだす」というのはおかしいと思います. 等速直線運動ではないので力は釣り合っていないからです． 物体には重力と垂直抗力Nがはたらきますが，半球上を滑っている間は（不等速）円運動をしているので，重力の半径方向の分力と垂直抗力との合力が向心力になっています． 従って次の式が成り立ちます．
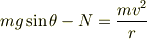
一般に垂直抗力N≧0 ですが，物体が球面から離れる瞬間には N=0 になるので次の式が成り立ちます．
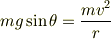
これはbeneさんが導かれた式（を速さv用いて表したもの）です．
次に，力学的エネルギー保存則を用いれば，右辺の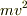 
をθの関数として表すことができます．
初速度が分かりませんが0なのでしょうか？実際に計算してみれば分かりますが，初速度が0の場合は簡単な計算でsinθの値が求まり，それを用いて高さが計算できます．
