微分記号
微分記号
yamainu さんの書込 (2007/07/22(Sun) 15:26)
こんにちは.よくこのサイトを参考にさせてもらってます 質問があります. 微分方程式のところを見ていた時, 両辺にdxをかける,という表現がありましたが,このような計算を していいのはなぜですか?dy/dxで一つの記号ではないのでしょうか
dy/dxを分数のように扱うのはぼくも自然とやっていたのですが, イマイチわからなくなってきました
Re: 微分記号
zoro さんのレス (2007/07/22(Sun) 17:13)
yamainuさん,初めまして.
数学はあまり詳しくないのですが,手元に今年度の高校の教科書,「新編 数学III,数研出版,ISBN4-410-80165-1」があり,そのp137に,「発展学習指導要領の範囲外の内容/3. 微分方程式」のなかに,次の様な例題が示されていますので引用します.
〜〜〜〜引用開始〜〜〜〜
● 例6kを常数とする時,次の微分方程式を解いてみましょう.

[1] 定数関数 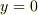 は明らかに解である.
[2]
は明らかに解である.
[2] 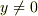 のとき,方程式を変形すると
のとき,方程式を変形すると

よって
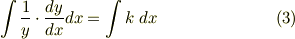
左辺に置換積分法の公式を適用すると
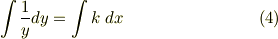
故に....
以下略.
一般に,

の形に変形出来る微分方程式の解は,次の等式から求める事が出来る.
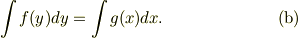
〜〜〜〜引用終了〜〜〜〜
私見では,式(a)と式(b)の間には,式(a)の辺々に 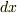 を掛けると,
を掛けると,

のように,左辺は  だけの関数,右辺は
だけの関数,右辺は  だけの関数に分離出来るので,次式のように左右独立に積分が可能となる.
だけの関数に分離出来るので,次式のように左右独立に積分が可能となる.
#このような場合を,変数分離型の微分方程式と呼ぶ.
といった説明の方が,直裁であるように思います.
〜〜〜
元に戻って,式(1),

の辺々に 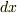 を乗じ,yで除すれば,;
を乗じ,yで除すれば,;

だから,辺々を,それぞれ独立に積分出来るので,次の式(3)が得られる,以下略.
とした方が,式の視認性は向上すると思います.
〜〜〜
詳しくは,数学の詳しい方のご説明をお待ち下さい.
Re: 微分記号
Joh さんのレス (2007/07/23(Mon) 01:46)
yamainuさん,
(yが微分可能で,dy/dxが一つの値に決まるという前提のもと)dy/dxは,dyとdxの分数だと思ってよいです.微分とは,そもそも?yと?xの比の極限です.この記号法はライプニッツ考案によるものですが, 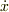 と書くニュートンのものよりも,分数のように計算できるという点で便利だし,微分の意味が明快だと思います.
と書くニュートンのものよりも,分数のように計算できるという点で便利だし,微分の意味が明快だと思います.