万有引力の問題

万有引力の問題

リッチ さんの書込 (2007/07/21(Sat) 23:57)

こんばんは．リッチと申します．よろしくお願いいたします． 早速ですが以下の問題を解いていてよくわからないのでご教授願えればと思い書き込みました．物理は嫌いではないのですが苦手です（汗）

質量M，半径Rの一様密度の惑星がある．この惑星の直径に沿って細いトンネルを掘る．但しトンネルは十分細くその部分の体積は無視できるとする．このとき次の問に答えよ．但し万有引力定数をGとする． (1)トンネルに沿ってx軸を取り，惑星の中心を通ってx軸に垂直にy軸を取る．x軸上の点(x,0)(但し-R≦x≦R)に質量mの質点を置いた．この質点が惑星から受ける万有引力F(x)を計算せよ．但し，この万有引力はこの惑星の内部の半径|x|の球の部分の質量が惑星の中心に集中しているとしてそれがこの質点に及ぼす万有引力と等しい． (2)この万有引力による位置エネルギーU(x)を求めグラフを書け．なおU(R)=U(-R)=0とする． (3)時刻t=0に質点mをx軸上の点(R,0)において初速度0でx軸上を運動させる．質点mに対する運動方程式を書け．そしてこの運動方程式を解き質点mのx座標を時刻tの関数として表せ．

先生曰く，数年前の東大の問題を改題したそうです．正直全くわかりません…．どう手をつけたら良いのでしょうか． どなたかご教授下さい．お願い致します．

Re: 万有引力の問題

クロメル さんのレス (2007/07/22(Sun) 01:44)

こんばんは，リッチさん．

まずは，一番のヒントだけ．

万有引力は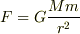， F=G\frac{Mm}{r^2} ですね． 質点が受ける惑星の引力は，半径ｒにおいては，半径ｒ以下の部分からしか，引力を受けません．よって，球の体積の公式を用いて半径r以下の部分の体積を表してください．そこに密度を掛けてやれば，その部分の質量Mが求まります． それを，万有引力の公式に代入してください．

Re: 万有引力の問題

リッチ さんのレス (2007/07/22(Sun) 02:03)

クロメル様，よろしくお願いいたします．

密度をρとする．半径|x|の球内部の質量は(4/3)π|x|^3ρとなるので万有引力はF(x)=G{(4/3)π|x|^3ρ×m}/x^2

というのでいかがでしょうか？

Re: 万有引力の問題

クロメル さんのレス (2007/07/22(Sun) 02:56)

そのとおりです．

x^2=|x^2|なので，約分してください． すると，中心に向かって，|x|に比例する力が働きますね． 中心の零引力を境に反対向きの力ですから． 結局，x軸にたいして，F=-kx(kは定数) の運動方程式が立ちます．

あとは，単振動の方程式同様にポテンシャルが定義できます．

分からなかったら，きいてください．

Re: 万有引力の問題

リッチ さんのレス (2007/07/22(Sun) 03:37)

クロメル様，迅速に解答して頂き有難うございます． (2)以降はもう遅いのでまた後で解こうと思いますが，先の問題で一つ質問させてください．この問題には惑星の密度ρは書かれていません．つまり自分で置いた文字になると思うのですが，これはこのままでよいのでしょうか？普通だったら問題文に「密度をρとする」などと書いてあると思うのですがこの問題には書いていないのです．

Re: 万有引力の問題

CO さんのレス (2007/07/22(Sun) 07:04)

リッチさま

> この問題には惑星の密度ρは書かれていません

全体の質量 M ，半径 R ，密度一様から求められます． 球の体積の公式はご存じですよね．

Re: 万有引力の問題

リッチ さんのレス (2007/07/22(Sun) 15:13)

tip★様，サイトのご紹介有難うございます．参考にさせて頂きます．

CO様，朝早くよりコメント有難うございます． ご指摘の所ですが，密度ρはρ=(3M)/(4πR^3)となるので万有引力F(x)はF(x)=(GMm|x|)/R^3となったのですがどうでしょうか？

また(2)ですが，万有引力の位置エネルギーはU=-GMm/rで表せるのでこの問題の場合U(x)=(-GMm|x|^2)/R^3だと思うのですがいかがでしょうか？

よろしくお願いいたします．

Re: 万有引力の問題

クロメル さんのレス (2007/07/23(Mon) 16:49)

返信遅れてすいません．

そうですね．引力の絶対値はあってます． x軸をとるという話なので，符号まで考えると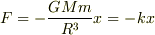， F=-\frac{GMm}{R^3}x=-kx です．

そして，ポテンシャルは係数がすこし違ってます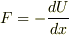． F=-\frac{dU}{dx} が定義なので，

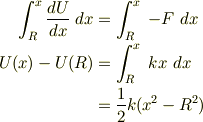
\int_R^x \frac{dU}{dx}\ dx &= \int_R^x \ -F \ dx \\U(x) - U(R) &= \int _R^x \ kx \ dx \\&= \frac{1}{2}k(x^2-R^2)

です．あとは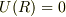， U(R)=0 を代入してください．

Re: 万有引力の問題

ｙama さんのレス (2007/07/23(Mon) 17:48)

ポテンシャルには付加定数の不定性があるので，基準のとり方には任意性がありますね． クロメルさんのように U(R)=0 になるようにとることもできますが，U(0)=0 になるようにとったほうが，平衡点（振動の中心）でポテンシャルが0になるので，都合がよいと思います．

Re: 万有引力の問題

クロメル さんのレス (2007/07/23(Mon) 18:32)

あ，いえ．リッチさんの最初の書き込みの問題文中にポテンシャル基準点の指示があったもので (^^;

Re: 万有引力の問題

yama さんのレス (2007/07/23(Mon) 19:03)

なるほど，そうですね．失礼しました．

Re: 万有引力の問題

リッチ さんのレス (2007/07/25(Wed) 23:17)

返信が遅くなってしまい申し訳ありません． 一つ質問なのですが， ＞x軸をとるという話なので，符号まで考えると というのがよくわかりません．恐縮ですがご教授願えればと思います． ご指摘の（２）ですが，クロネコ様の書き込みのように解くと，U(x)={GMm(x^2-R^2)}/2R^3となりまして，グラフを書くと切片が-GMm/2Rの放物線となりました．いかがでしょうか？ また（３）については単振動になると思うのですが上手くアプローチできません．本当に申し訳ありませんが，教えて頂きたく思います．

よろしくお願いいたします．

Re: 万有引力の問題

クロメル さんのレス (2007/07/27(Fri) 02:00)

お気になさらず，忙しい時はそんなもんですから．

（１）まずは，符号についてですね． そうですね，ちょっと言葉不足でしたでしょうか． まず，x軸の正の向きを決めます． そして，力の働く向きの正の方向をきめるのですが， 運動方程式は 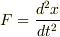F=\frac{d^2x}{dt^2} というふうに， xの座標と結びついていますから， x軸の座標がきまると，力の正の方向はx軸の正の方向と同じになります．

すると，xが正のとき，x軸の負の方向に（力の働く向きの負の方向に）位置に比例する力が働くことは（今回はそうなってますね．）働く力＝-kxと表せます．

逆に，xが負のときは，正の方向に力がかかり，位置が負，力が正ですから， やはり-kxと表せます．こうして両方の場合分けはいらず，絶対値が取れます．

（２）ポテンシャルの形について． そのとおりです．両端が値０で，負の方向にでっぱった放物型ポテンシャルとなります．

（３）これは，大学受験の知識で解くには，単振動がsinやcosで表わされるということを利用するのでしょう． 覚えるべきことは，

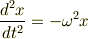
\frac{d^2x}{dt^2}=-\omega^2 x

（ただし 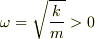\omega=\sqrt{\frac{k}{m}}>0 等とする） で表わされる運動方程式の解は，

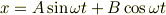
x=A\sin \omega t + B \cos \omega t

もしくは，

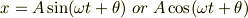
x = A \sin (\omega t + \theta) \ or \ A \cos(\omega t + \theta)

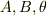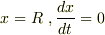ここで， A,B,\theta は，ある定数です． 二つの表現は，下の式に三角関数の加法公式を用いれば，上の式になりますね． 上の式の方が扱いは簡単かな？ あとはt=0で， x=R\ , \frac{dx}{dt}=0 となるように， A,Bもしくは，A,θを求めてください．

これで伝わればよいのですが．

Re: 万有引力の問題

リッチ さんのレス (2007/07/27(Fri) 06:46)

クロメル様，ご丁寧な解答本当に有難うございました． お陰様で理解することが出来ました． 今後とも精進していきます． またクロネコ様のHPを拝見させて頂きましたが，勉強に対する姿勢が本当に素晴らしく，私もクロネコ様のように頑張らなければと思いました． 今回は本当にどうも有難うございました．またよろしくお願いいたします．

Re: 万有引力の問題

クロメル さんのレス (2007/07/27(Fri) 11:20)

どういたしまして，解決してよかったです． そして僕のホームページが，そのような形で役に立てて光栄です（＾＾；） それではまた何かあったら，その時はよろしくお願いします．