カイ さんの書込 (2007/07/20(Fri) 11:57)

こんにちは． いままで，シュレディンガー方程式と条件の関係を気にせずに， どんどん条件を使っていたのですが，未知数と条件の数の関係を知りたくなりました． 未知数は基本的に，固有値Eが一つ，二階微分による定数が２つ，の３つだと思うので， 境界条件が３つあればいいのかな，と考えましたが， 実際は，境界条件２つと規格化条件１つで決まる場合もあります． しかし，規格化条件は波動関数特有の条件なので，他の２階微分固有値方程式だとどうなのか疑問です． また，有限な井戸型ポテンシャルの場合は，波動関数が滑らかである条件(これも境界条件の一種でしょうか？)でグラフからEは求まりますが 任意定数は最後までもとまらなかったりして，ますます，未知数と条件の関係がわからなくなります．

支離滅裂な文章で申し訳ありません．

ｙama さんのレス (2007/07/20(Fri) 14:41)

シュレーディンガー方程式は偏微分方程式なのでその解は一般には任意関数を含みます．

特別な場合として，1次元の定常状態の方程式は２階の常微分方程式になるのでその解は２個の積分定数を含み，境界条件や規格化条件によって決定されます． 同時に，エネルギー固有値も境界条件から決まりますが，これは積分定数として現れる定数ではなく，初めから方程式に含まれている未定の定数です． すなわち，この場合は３つの条件（２つの境界条件と規格化条件）によって３つの定数（エネルギー固有値と２つの積分定数）が決まるわけです．規格化する場合は，３つの境界条件を課することはできません． また，条件が足りなければ，未定定数が残る場合もあります．

カイ さんのレス (2007/07/20(Fri) 20:23)

返信ありがとうございます ＞同時に，エネルギー固有値も境界条件から決まりますが 同時に，というのは，この条件で任意定数が決まり，この条件で固有値が決まる というようなことでなくセットで決まる，ということでしょうか．

弦を２箇所固定すると，定常波が現れることからも，２つセットの境界条件があって ２番目の境界条件で固有値が決まる，ということであってますか？

でも，調和振動子の「波動関数が発散しないためにエルミートの漸化式が途中で切れる」 というのは条件が一つなのにエネルギー固有値が求まってしまいます．

yama さんのレス (2007/07/21(Sat) 00:12)

>同時に，というのは，この条件で任意定数が決まり，この条件で固有値が決まる というようなことでなくセットで決まる，ということでしょうか．

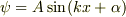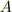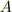エネルギー固有値は境界条件によって決まり，規格化条件には無関係ですが任意定数については一概には言えません． 簡単な場合として，１次元のポテンシャルの箱で，外部のポテンシャルが無限大の場合を考えましょう． この場合の解は， と表されます． ただし， はエネルギー固有値に関係する定数で と は任意定数です． 境界条件によって と が定まり，次に規格化条件によって が定まります． 一方，a,bを任意定数として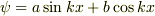， の形に表すこともできます．このときはa,bのどちらかが0になる場合を除けば，境界条件と規格化条件を同時に用いることによっててa,bが決まることになります．

>弦を２箇所固定すると，定常波が現れることからも，２つセットの境界条件があって ２番目の境界条件で固有値が決まる，ということであってますか？

これも同様に考えれば，２つの境界条件によって固有値が決まることになりますが，２番目の境界条件で決まるとは必ずしも言えないと思います．

>でも，調和振動子の「波動関数が発散しないためにエルミートの漸化式が途中で切れる」 というのは条件が一つなのにエネルギー固有値が求まってしまいます．

境界条件は+∞と-∞で波動関数が発散しないということなので，これは２つの条件です．さらに規格化条件を合わせると，全部で３つの条件があります． この３つの条件によって，エネルギー固有値と２つの任意定数が定まります． と言うと２つの任意定数はどこにあるのかと思われるかもしれませんが，これは級数の各項の係数として含まれています．もちろん係数は無限個ありますが，初めの２つが決まれば残りの係数は漸化式によって決定されるので，任意定数は２つだけです． なお，境界条件を満たすためには有限個の係数を除く残りの係数がすべて0にならないといけないことはご存じの通りです．

カイ さんのレス (2007/07/21(Sat) 00:20)

詳しくありがとうございます． 調和振動子については納得しました．

任意定数は，一つの条件で決まりますが 固有値を決めるには，一つの固有値でも２つの条件がないと駄目なのでしょうか？ もちろん，２つの条件のうちの一つが任意定数を決めるというのはわかっていますが，一つだけの条件で固有値を決めるのは不可能ですか？という意味の質問です．

yama さんのレス (2007/07/21(Sat) 01:06)

それはできないと思います． x軸上の１点だけで波動関数の値または波動関数の微分の値が分かっても，それだけではエネルギー固有値は決まらないと思います．

カイ さんのレス (2007/07/21(Sat) 22:52)

なるほど・・・． 未知数の数と条件の数については，一対一に対応している(未知数の数＝条件の数)なのに，固有値は２つセットの条件じゃないと決まらないんですね・・・． なんか不思議です．数学的なちゃんとした理論があるのでしょうか． 物理的に考えれば，２つの境界条件を課すということは，粒子を束縛することだと思うので納得できますが．

しかし，今まで闇雲に解いていましたが，なんとか整理できました． ありがとうございました．