ei さんの書込 (2007/07/17(Tue) 03:03)

はじめまして，eiといいます．現在高３です． ひと通り高校物理の範囲を授業で終えたところなんですけど，高校物理は公式が天下り的に与えられることが多いように思います．今受験のために物理も演習をしてるんですけど，磁束変化により起電力が生じるということや，磁場によって動く電荷に進行方向に垂直な力が及ぶ，といったことが自分でうまく説明できません．自分なりに本で調べたんですけど，ローレンツ収縮だとか相対論が絡んでいたりして，数式も何やら複雑そうで・・・何より受験生なもので，こういうことばかり調べている時間もないんです．かといって理解もしていない公式を使うのも気持ち悪いので演習に入れないでいます． クーロンの法則だけを前提として，磁場の定義，電磁誘導の法則，ローレンツ力などが感覚的に納得できるような説明はないものでしょうか．もし知っていたら教えていただけるとすごく助かるのですが・よろしくお願いします．

イレフト さんのレス (2007/07/17(Tue) 03:56)

磁場の定義やローレンツ力などはたぶん実験事実といった面が強いかと．． ゲージ理論からは導けたような気がしますがやっぱり難しいでしょう．

ただ，高校での磁場の公式などはわりと簡単に導けますよ．拙いものですが下のHPで電磁気のまとめものせているのでよかったら見てください．高校生にはちょっと難しい部分もあるかもしれませんがそのときは気軽にHPの連絡先に聞いてください．

ei さんのレス (2007/07/17(Tue) 23:09)

イレフトさん，お返事ありがとうございます．

＞磁場の定義やローレンツ力などはたぶん実験事実といった面が強いかと．． そうなんですよね．受験参考書でも”高校生のうちは実験則として覚えておけばよいでしょう”みたいなことしか書いてありませんし．．でも磁場を電荷から独立したものとして考えているような気がしていまいち納得できないんです． 磁場は電荷の運動により生じる場ですから，クーロンの法則だけ認めれば，感覚的に（数式を使わずして）ローレンツ力などの意味は理解できるような気がするんですけど，甘い考えでしょうか．

zoro さんのレス (2007/07/17(Tue) 23:45)

eiさん，初めまして．

なかなか鋭いセンスでお考えになっていますね．自分は大昔，高校の教科書に馴染めず，無視して独学したので，すこし気持ちが判る気がします．

今年度の物理や数学の高校の教科書を眺めていますが，物理の教科書はとても中途半端に広すぎる分野を書きすぎていて，散漫だと，私は思います．といっても，受験との兼ね合いで，目を瞑って行きましょう．入学したら，思う存分に勉強と考察をする事ができるのですから．

＞磁場は電荷の運動により生じる場ですから，クーロンの法則だけ認めれば，感覚的に（数式を使わずして）ローレンツ力などの意味は理解できるような気がするんですけど，甘い考えでしょうか．

ある意味，正論と思いますが，達成するには難しいと思います．何が難しいかと言えば，「感覚的に（数式を使わずして）」こそ一番の課題だからです．「直感的に理解する」のと「感覚的に理解する」のも違うように思います．たとえば；

<pre> ＜＜＜ヒトが自然を理解する二重構造＞＞＞ . . . ＿＿＿＿*でも，巧く行くと「素晴らしい解釈」が可能． ／意外と難しい！！ ｜ 物理現象 ｜←ーーーーーーーーーー直接(感覚)的な観察・理解ーーーー┐ ＿＿＿＿／ ＿＿＿＿├ーーヒト ↑ ／｜ 〜〜〜 └ーーー｜数学モデル｜←ーーー間接(数学)的な観察・理解 ーーー┘ 意外と楽〜 ＿＿＿＿／

*でも，物理数学という道具箱の整備が必要． *さらに，一部の検討から，広範な部分への一般化という果実を得る事もある． </pre>

話を戻します； お書きになった例では，クーロンの法則は「静止状態の電荷」の様子を記述するのは確かです．勿論それを，相対的に運動する系から見えれば電流分布に見えますよね．それを計算しようとすると面倒な式になり，初心者さんには見通しが悪いものになります．

さらに，コイル見たいな例では，環状の金属線に分布した電荷が「円運動」という加速系への変換を必要とします．

という訳で，eiさんのグランド・デザインを実施するには，考える以上に困難があると思います．でも，だからといって，このアイデアを否定するものではありません．むしろ，eiさんが，将来に於いて，色々な表現方法を駆使して，中学生・高校生・大学生などの広い範囲の生徒・学生にむけて説明出来るようになって戴くと善いかと思います．

【追伸】

書いた後，これを眺めながら自分の若い頃を思い出すと，自分の欠点は，数式は天から与えられたツールと考えて，深い理解を避けて来たように思います．特に，高校生から学部生の頃は，徹底して「数学の利用」を心がけていて，数学事典のようなものを数冊準備して，物理の問題に合わせて，ページを巡るようにしていました．

その代わり，物理の問題に付いては，複数の見方をするようにしていました．ですので，問題を考えるのは好きだったのですが，与えられた時間内に答えが見つかる確率が低いのが辛かったです．そう，試験で点数を取れなかったのです．

その後，紆余曲折して，こちらのサイトで数学と物理との関係を見直す事が出来たり，忘れていた物理を思い出したりして，上に示したイメージが出来ました．

多くの方は，若い頃には「数学を駆使して，物理にアプローチ」する場合の事が多いように思います．その場合は，洗練された数式を使いたくなると思うのですが，たまには，直感的，感覚的なイメージと数式の関係を検討するのも善いと思います．

また，イメージというのは，絵にすると考え易くなると思います．リアルな絵，作図のような絵，ポンチ絵，イラストレーション，漫画，アニメーション，3Dアニメーション等々，多くの表現法を使って，説明すると面白いと思えます．

yama さんのレス (2007/07/18(Wed) 00:05)

例えば，静止した電荷のつくるクーロン電場をローレンツ変換すると等速直線運動する電荷のつくる電磁場になります．この場合の磁場はビオ・サバールの法則に従います． 加速度運動をする電荷のつくる電磁場を求めるのはかなり難しくなりますが，これも基本的には，静止電荷によるポテンシャルを運動電荷にも適用できるようにローレンツ共変な形に表すことによって，導くことができます． また，ローレンツ力も，電磁場のローレンツ変換を利用して導くことができます．

しかし，このようなことを感覚的に（数式を使わずして）理解するのは難しいと思います． むしろ，数式の助けを借りることによって，ある程度は感覚的にも理解できるようになるのではないでしょうか．

ei さんのレス (2007/07/18(Wed) 13:11)

zeroさん，yamaさんお返事ありがとうございます．

＞zeroさん ＞受験との兼ね合いで，目を瞑って行きましょう．入学したら，思う存分に勉強と考察をする事ができるのですから．

おっしゃるとおりですね．今年大学に入れなければもう１年受験勉強続けなければならないわけですし．納得いかないところもありますけど，これ以上このことを追求したとしても受験で物理の本質が問われるようなことはないですし（それが一番悲しい，というより腑に落ちない部分ではありますが）とにかく今は受験勉強に専念して大学に入って時間ができたらじっくり考えようと思います．zeroさんの意見とても参考になりました．ありがとうございました．

＞yamaさん ＞むしろ，数式の助けを借りることによって，ある程度は感覚的にも理解できるようになるのではないでしょうか．

なるほど．．自分は直感的に理解することにこだわりすぎてしまったのかもしれません．確かに数式を用いて考えているうちに感覚的にわかってくることはよくありますね．そこが物理の面白いところですし．ただローレンツ変換などは本で読みましたが，ちゃんと理解するには今の自分には時間が足りないと感じました．大学に入っても物理をやりたいと思ってるので，時間ができたら勉強したいと思います．ありがとうございました．

皆さんの意見とても参考になりました．すごい助かりました．今は割り切って受験勉強をやろうと思います．本当にありがとうございました．

zoro さんのレス (2007/07/18(Wed) 18:22)

eiさん，

＞受験で物理の本質が問われるようなことはないですし（それが一番悲しい，というより腑に落ちない部分ではありますが）

ご指摘の通りだと思います．この問題の本質は，教育というものを一定の枠の中に収めようという不自然な形態を続ける限り止まらないと思います．

ところが，近年の国立大学→独立行政法人の流れから，嫌でも各大学が良い人材を捜す動きを生じていると思います．最終的には，大学の入試の改革，それを受けた高校・中学・小学といった教育体系に変革が広がった時に，どのようなモデルを提案出来るかに掛かるでしょう．なにも「大手の塾」だけにそれを委ねないで，この数式掲示板などからも，多いに教育モデルの提案をすれば良いのだろうと思います．

このような過渡期である事を意識した上で，なおかつ，受験勉強にチャレンジして下さい．

zoro さんのレス (2007/07/18(Wed) 19:47)

eiさん，

一つ提案が在ります．受験勉強で「納得しがたい物理」を勉強する「高校生としてのご自身の見解」を「将来，物理の教科書を作ろうとするご自身への投稿」として書くのはどうでしょうか．

もちろん，その様な意見を書くうちに，疑問を生じたら，ここに質問すれば善いですよね．多くの方々から意見を戴けると思いますし...．

通りすがりのトクメイ希望 さんのレス (2007/07/18(Wed) 20:28)

通りすがりが割り込んで申し訳ありません．

eiさんの発言を読んで， いまでも物理に対してこのような心意気を持った方がいる， ということに大変感心しました．

少しばかり長生きしている者のおせっかいですが， もし受験勉強を突破して大学に入学されたら， ぜひ「ファインマン物理学」を読まれることをお勧めします． この中に，きっとお探しの答えがあると思います．

小林＠那須 さんのレス (2007/07/19(Thu) 08:59)

yamaさん>加速度運動をする電荷のつくる電磁場を求めるのはかなり難しくなりますが，これも基本的には，静止電荷によるポテンシャルを運動電荷にも適用できるようにローレンツ共変な形に表すことによって，導くことができます．また，ローレンツ力も，電磁場のローレンツ変換を利用して導くことができます．

同意します．電位とベクトル・ポテンシャルの四元電磁量 <i φ,A> は，原点の静止電荷 q に対して <i q/(4`π r), 0,0,0> とできます．この四元ベクトルを Lorentz 変換してやれば動いている電荷による <i φ,A> が作れます．これらの四元ベクトルの線形な重ねあわせてやるで，一般の場合の 四元電磁量 <i φ,A> が導けます．一般の場合の <i φ,A> が導ければ，E, H が導けます．四つの Maxwell 方程式が導けます．

ローレンツ力については <i φ, A> と四元速度の内積がスカラー・エネルギーになることより導けるはずです．電荷 q と その四元速度 u4 から scalarE = < <i φ, A> | q u4 > > が作れます．これに対し四元微小位置変化 Δl4 と四元力 F4 は ΔscalarE = <F4 |Δl4> を満たすとできます．これからローレンツ力が導けるはずだと思うのですが，まだ思っているだけです．

ここらの話は普通の高校生では無理だと思います．でも ei さんが行列・ベクトル空間を理解できていて，四次元空間での直交などの幾何学的イメージが持てるのならば可能な話だとも思います．

yamaさん>しかし，このようなことを感覚的に（数式を使わずして）理解するのは難しいと思います． yamaさん>むしろ，数式の助けを借りることによって，ある程度は感覚的にも理解できるようになるのではないでしょうか．

数式で理解できれば，そのほうがベターなのは同意します．でも多くの場合，数式の理解自体が難しい作業です．私は昔，解析数学の基礎だと思って Lebesgue 積分に力を注いだことがあります．その多くが時間の無駄だったと今は後悔しています．ですので単純に数式に拘ることを心配します．

現代のコンピュータ・パワーを使えばラマヌジャン級の計算力が誰でも持てます．三次元グラフの作成など簡単です．コンピュータ・パワーを活用できる現代では数値実験による理解も活用すべきだと主張します．

通りすがりのトクメイ希望 さんのレス (2007/07/19(Thu) 10:46)

> 磁場は電荷の運動により生じる場ですから，クーロンの法則だけ認めれば， > 感覚的に（数式を使わずして）ローレンツ力などの意味は理解できる > ような気がするんですけど，甘い考えでしょうか．

またまたお邪魔します． eiさんのこの発言は注目に値しますね． ローレンツ力はクーロン力から導けるのでは・・・という 考えだと思いますが，まさにそのとおりです． ただし，その理解のためには相対性理論の考え方や， ローレンツ収縮を理解することが前提となります．

直線電流によって作られる磁場を考えると，電流の周りに 渦巻く場となっています．その磁場に電子が飛び込むと， 直線電流から離れる（あるいは引き付けられる）運動を示します． もし，電流（＝電荷の運動）の速度に一致する座標で電流を観測したら， 電荷は流れていません．しかしローレンツ収縮により電荷密度は 変化しています．電荷密度が正負の電荷で異なっているので， （なにしろ電流として流れているのは電子だけなので） クーロン力が働くわけです．これが通常の座標では ローレンツ力として見える，ということです．

これって，ファインマン物理学の本に書いてあるんです． ファインマンはすごいです． 自然を物理的に理解するとはどういうことか，教えてくれます．

ｙama さんのレス (2007/07/19(Thu) 12:34)

>ローレンツ力については <i φ, A> と四元速度の内積がスカラー・エネルギーになることより導けるはずです．電荷 q と その四元速度 u4 から scalarE = < <i φ, A> | q u4 > > が作れます．これに対し四元微小位置変化 Δl4 と四元力 F4 は ΔscalarE = <F4 |Δl4> を満たすとできます．これからローレンツ力が導けるはずだと思うのですが，まだ思っているだけです．

エネルギーは３次元ではスカラーですが，４次元ではスカラーではなく，４元ベクトルの１成分です．４元ポテンシャルと４元速度の内積は４次元スカラーになりますが，それをスカラー・エネルギーとよぶのは不適切だと思います． よびかたはともかくとしても ΔscalarE = <F4 |Δl4> という関係は成り立ちませんし，この関係からローレンツ力を導くこともできないでしょう．

小林＠那須 さんのレス (2007/07/20(Fri) 08:50)

>ΔscalarE = <F4 |Δl4> という関係は成り立ちませんし，この関係からローレンツ力を導くこともできないでしょう．

厳密にはローレンツ力を導けないことに同意します．元々ローレンツ力は共変ではないからです．でも 1`km/`sec 程度の速度の電荷に働くローレンツ力を数値実験によって 6 桁程度の精度で導くことはできるはずです．

厳密な意味では， Lorentz 変換から共変ではないローレンツ力を導けないと思います．共変な Lorentz 力しか導けないと思います．yama さんはどんな意味で「ローレンツ力も，電磁場のローレンツ変換を利用して導くことができます．」と主張されますか？

ミュフ猫 さんのレス (2007/07/20(Fri) 10:55)

>Lorentz 変換から共変ではないローレンツ力を導けないと思います． >共変なLorentz 力しか導けないと思います．

横レス失礼します．ローレンツ力は「共変ではない」ものと「共変な」ものが あるのでしょうか？それとも，「ローレンツ力」と「Lorentz 力」とは別の 物理量を意味しているのでしょうか？

ｙama さんのレス (2007/07/20(Fri) 11:44)

小林＠那須が書かれた関係は一般には成り立ちませんが，磁場が一様で時間的に変化しない場合にはなりたち，ローレンツ力が導かれるようです．

ローレンツ力と電磁場のローレンツ変換の関係については，たとえば次のようないろいろなサイトに説明があります．

• http://home.catv.ne.jp/dd/pub/grav.html#3
• http://www.h3.dion.ne.jp/~spstring/Special_theory_of_relativity/Special_theory_of_relativity-node16.html

小林＠那須 さんのレス (2007/07/21(Sat) 08:45)

>それとも，「ローレンツ力」と「Lorentz 力」とは別の 物理量を意味しているのでしょうか？ 同じ物理量です．

共変な Lorentz 力は下のように表せます．

F4= │ 0, i Ex, i Ey, i Ez│ │-i Ex, 0, Hz, -Hy│ │-i Ey, -Hz, 0, Hx│ │-i Ex, Hy, -Hx, 0│

としたとき，四元力 Force4 と 四元速度 u4 と 電荷 q の間に次の関係があります．

Force4 = q F4 u4

>小林＠那須が書かれた関係は一般には成り立ちませんが

私は上の Force4 が ΔscalarE = <Force4 |Δl4> の関係にもあると思っています．こちらの方が，より根源的だとも思っています．

力 = ΔscalarE/Δl4

だからです．yama さんが一般に成り立たないとする反例，または理由を教えてもらえますでしょうか．先の URL では成り立たない理由になっていません．

yama さんのレス (2007/07/21(Sat) 12:02)

間違っていたところがありましたので，まずおわびして訂正しておきます． 磁場が一様で時間的に変化しない場合には小林＠那須が書かれた関係がなりたつと書きましたがこれは間違いでした．

小林＠那須さんの定義では 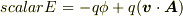になると思います．従って，力 = ΔscalarE/Δl4 の空間成分は次のようになります．

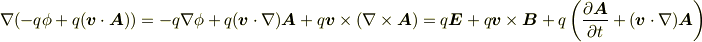
これは，ローレンツ力に似ていますが，第３項があるためローレンツ力ではありません．第３項が0になる場合，すなわち電荷の運動にともなって 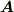が変化しないときにはローレンツ力になります．

なぜローレンツ力にならないかというと，上で計算したものは通常の力ではなく一般化された力だからです． 通常の力は運動量の時間微分に等しいのですが，一般化された力は一般化運動量の時間微分に等しくなります． 一般化運動量の時間微分を計算すると，通常の運動量に上の式の第３項を加えたものになり，その結果運動方程式では第３項がキャンセルしあって，通常の力としてはローレンツ力だけが残ります．

ミュフ猫 さんのレス (2007/07/21(Sat) 12:47)

>>それとも，「ローレンツ力」と「Lorentz 力」とは別の >>物理量を意味しているのでしょうか？ >同じ物理量です． > >共変な Lorentz 力は下のように表せます． > >F4= │ 0, i Ex, i Ey, i Ez│ >│-i Ex, 0, Hz, -Hy│ >│-i Ey, -Hz, 0, Hx│ >│-i Ex, Hy, -Hx, 0│ > >としたとき，四元力 Force4 と 四元速度 u4 と 電荷 q の間に >次の関係があります． > >Force4 = q F4 u4

レスどうもありがとうございます．なるほど．

小林＠那須 さんのレス (2007/07/21(Sat) 13:08)

御返答ありがとうございます．細かい検算まではできていませんが，yama さんが言っている意味は理解できたと思います．

たぶん v は静止座標系の時間で測った速度なのでしょう．Δτ = root(Δs^2) で計った速度ではないのでしょう．

>一般化運動量の時間微分を計算すると，通常の運動量に上の式の第３項を加えたものになり，その結果運動方程式では第３項がキャンセルしあって，通常の力としてはローレンツ力だけが残ります．

こんな微妙な関係があるなんて知りませんでした．ありがとうございました．

yama さんのレス (2007/07/21(Sat) 13:13)

小林＠那須さんのscalarE は，４元ポテンシャルと４元速度の内積なので，

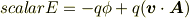
ではなくて，右辺に 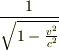を掛けないといけないようですね． しかし v<<c の場合の非相対論的近似では，この乗数は１と見なせるのでやはり前記のように言えるでしょう．