Jack さんの書込 (2007/07/15(Sun) 11:24)

Si中にP(リン)を１０^16 cm^-3 ,B(ホウ素)を３*１０^16 cm^-3 添加した．

（１）この半導体の電子及び正孔の密度を求めよ．ただし，Siの真性キャリア濃度Niを1.5*10^10 cm^-3 とする．

この問題を解いてみたところ，電子の密度ｎ＝０ 正孔の密度ｐ＝2.0*10^16 になってしまいました．

電子の密度が０になるということは有り得るのでしょうか？ またこの結果が正しくないならば，どのように解けばよいのでしょう？

tip★ さんのレス (2007/07/15(Sun) 12:41)

この問題は，室温ということでよろしいですか？

とりあえず，室温という条件下の場合で考えたいと思います． 正孔密度はJackさんが書いている通りであっていると思います． 電子の密度が0になることはないと思います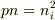． という式を使えば，電子の密度が出てくると思います．

自分も半導体を学んでまだ間もないのであっているかどうか微妙なので，zoroさん，または，篠原さんの返信をとりあえず待ってください．

Jack さんのレス (2007/07/15(Sun) 16:28)

何の条件も与えられてなにので，室温でいいのだと思います． tip★さんが教えてくれた公式でnを求めたところ， ｎ＝0.75*10^-6 となりました．よって，この半導体はｐ型半導体ということですよね？

tip★ さんのレス (2007/07/15(Sun) 17:30)

>>この半導体はｐ型半導体ということですよね？

その通りだと思います． アクセプタの濃度の方が大きいので，ドナーはアクセプタにより補償されるので，p形半導体となります．

Jack さんのレス (2007/07/15(Sun) 18:07)

ありがとうございます． ちなみに参考として聞きたいのですが，tip★さんは正孔の密度を求めるときにどような計算で求めましたか？

tip★ さんのレス (2007/07/15(Sun) 18:40)

とりあえず，簡単のためにアクセプタのみがドープされている場合を考えます．

Siは室温付近で飽和領域（出払い領域）にあります．（というよりトランジスタやダイオードのような半導体素子はこの領域で使用されるため，作為的にこの領域にされていると考えれます．）

飽和領域では正孔密度pは 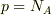です．

ドナー濃度よりもアクセプタ濃度のほうが大きいのでドナーはアクセプタにより補償され，アクセプタ濃度は になります． 上式より，アクセプタ濃度が正孔濃度になります．

つまり，アクセプタ濃度からドナー濃度を引いただけです．

Jaｃｋ さんのレス (2007/07/16(Mon) 22:29)

なるほど．理解できました．ありがとうございます．

追加で質問なのですが，この問題でフェルミ準位を求める時のNaというのは，添加したホウ素分の３*１０^16 cm^-3 でよいのでしょうか？

tip★ さんのレス (2007/07/16(Mon) 23:11)

補償という概念をよく理解すればわかるはずです．

補償により，どちらともイオン化されてます．このときキャリアは発生しません．しかし，アクセプタ濃度の方が大きいので，その分だけが正孔の濃度に関係するものになると思います．

篠原 さんのレス (2007/07/17(Tue) 00:10)

みなさん，こんにちは． 篠原です．

> ｎ＝0.75*10^-6となりました．

Jackさん，何かおかしいと思いませんか？ あなたの示した式によると，シリコンを 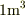，約2トン持ってくると，その中に自由電子は平均1個しかいないことになります． いくら純粋なシリコンでも，p形に偏ったシリコンでも，室温でこんなことは起こり得ません．

tip★さんが示した式は，

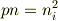
です．

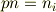
ではありません． 次元に注意してください．

また，物理量を書くときはその単位も書きましょう． 単位を含めて考えると，上のような間違いは防げたはずです．

tip★さん，

> （というよりトランジスタやダイオードのような半導体素子はこの領域で使用されるため，作為的にこの領域にされていると考えれます．）

少し補足しておくと，作為的に出払い領域で使用しているわけではなく，シリコンの場合，偶然室温付近が出払い領域だっただけです．

これらの温度領域は，バンドギャップと不純物のイオン化エネルギーに関係します． バンドギャップが小さければ，より低い温度で真性領域になってしまいます． （シリコンに比べてゲルマニウムがより低温で真性領域になるのはこのため） また，不純物のイオン化エネルギーが大きいと，不純物領域がより高温側までなります． シリコンの場合，バンドギャップがkTに比べてそれなりに大きく，かつ不純物のイオン化エネルギーがkTと同程度に小さいために，室温で偶然出払い領域となっているだけです．

ちなみに，青色LEDにも使われ，今もっとも盛んに研究されているGaN系の材料では，アクセプタのイオン化エネルギーが約200meVとかなり大きいため，室温では不純物領域となります．このため，数万個に1個の割合でアクセプタがイオン化して，これにより出てきた正孔により，かろうじてp形伝導が得られているという凄まじい世界の材料系です． こんな材料でも，まともに動くLEDやLDが量産されているんだから，すごいですねー．

tip★ さんのレス (2007/07/17(Tue) 00:40)

篠原さん，フォローありがとうございます．

>>これらの温度領域は，バンドギャップと不純物のイオン化エネルギーに関係します． バンドギャップが小さければ，より低い温度で真性領域になってしまいます． （シリコンに比べてゲルマニウムがより低温で真性領域になるのはこのため） また，不純物のイオン化エネルギーが大きいと，不純物領域がより高温側までなります． シリコンの場合，バンドギャップがkTに比べてそれなりに大きく，かつ不純物のイオン化エネルギーがkTと同程度に小さいために，室温で偶然出払い領域となっているだけです．

この部分はいつか聞こうと思っていた部分だったので助かりました．

>>ちなみに，青色LEDにも使われ，今もっとも盛んに研究されているGaN系の材料では，アクセプタのイオン化エネルギーが約200meVとかなり大きいため，室温では不純物領域となります．このため，数万個に1個の割合でアクセプタがイオン化して，これにより出てきた正孔により，かろうじてp形伝導が得られているという凄まじい世界の材料系です． こんな材料でも，まともに動くLEDやLDが量産されているんだから，すごいですねー．

半導体はやっぱり面白いですね．卒業研究はエネルギー系の方に行きたいなぁと思っていたのですが，半導体もなかなか捨てがたいですね．

tip★ さんのレス (2007/07/17(Tue) 01:22)

Jackさん，

すいません．間違ったことをおしえていたようです． 上でも言ったように自分は半導体を学んでまだ間もないです．色々間違うことはあると思いますが，そのときは教えられているからといって下手にでず，間違っているところは間違っていると指摘していただけると自分としてはうれしいです．

篠原さん，

>>ちなみに，青色LEDにも使われ，今もっとも盛んに研究されているGaN系の材料では，アクセプタのイオン化エネルギーが約200meVとかなり大きいため，室温では不純物領域となります．このため，数万個に1個の割合でアクセプタがイオン化して，これにより出てきた正孔により，かろうじてp形伝導が得られているという凄まじい世界の材料系です． こんな材料でも，まともに動くLEDやLDが量産されているんだから，すごいですねー．

スレ違いと思いますが このように，この理論はこの部分で実用されていますよ的な記事を書いていただければかなり面白いと思います． 理学部の人がどういう考えをもっているのかわかりませんが，工学部の人（じぶんだけかもしれませんが）は，実用されている具体例を出せばかなり興味を持つのではないかと思います．

Jack さんのレス (2007/07/17(Tue) 11:35)

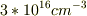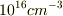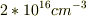＞tip★さん ではホウ素の添加分 と，リンの添加分 と差分の が 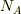になるということですか？

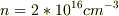
＞篠原さん すいません，たしかに見間違えてました．申し訳ないです． やり直してみたのですが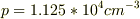， となりました．

篠原 さんのレス (2007/07/18(Wed) 11:27)

tip★さん

> 半導体はやっぱり面白いですね．卒業研究はエネルギー系の方に行きたいなぁと思っていたのですが，半導体もなかなか捨てがたいですね．

ぜひ，半導体分野へどうぞ！ ;)

> このように，この理論はこの部分で実用されていますよ的な記事を書いていただければかなり面白いと思います．
> 理学部の人がどういう考えをもっているのかわかりませんが，工学部の人（じぶんだけかもしれませんが）は，実用されている具体例を出せばかなり興味を持つのではないかと思います．

半導体の面白さがわかってもらえる方がいて，うれしい限りです． 記事を書くのは，忙しかったり，その他諸事情により休止しています． tip★さん，メンバーになって記事を書いてはいかがですか？

tip★ さんのレス (2007/07/18(Wed) 15:36)

Jackさん，

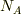はその値で良いと思います．厳密に言えば 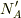と書き換えたほうがいいとおもいます．

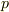, の値は逆じゃないですか？もう1回確かめてみてください．

篠原さん，

>>tip★さん，メンバーになって記事を書いてはいかがですか？

今は，基礎を固めて，知識を蓄えていって， いつかメンバーになって記事を書いてみたいと思います．

Jack さんのレス (2007/07/18(Wed) 22:44)

tip★さんありがとうございました． ｎとｐは書き間違いです．申し訳ありません