エネルギーと力（電磁気学）

home > 掲示板 >

このページのPDF版

サイトマップ

エネルギーと力（電磁気学）

tip★ さんの書込 (2007/07/14(Sat) 15:19)

平行平板コンデンサに電圧Vを与えたときに極板に働く力を求めよ．

この問題は，仮想変位を与えると静電容量が減少し，そのため電荷も減少するのでエネルギーの授受を考えなければなりません．

自分は，電源から供給されるエネルギーを変化後の静電容量をC’，変化前の静電容量をCとすると 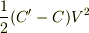$\frac{1}{2}(C'-C)V^{2}$ となりました．

正解は 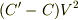$(C'-C)V^{2}$ でした．

なぜ正解のようになるのかがよくわかりませんでした．どなたか解説よろしくお願いします．

Re: エネルギーと力（電磁気学）

yama さんのレス (2007/07/14(Sat) 21:30)

コンデンサに蓄えられるエネルギーの変化だけでなく，発生するジュール熱も含めて考える必要があります．

Re: エネルギーと力（電磁気学）

zoro さんのレス (2007/07/14(Sat) 22:21)

まだ，どのよう考えればいいのか検討中ですが...．今の所，電極周辺を無視した平行板コンデンサ(真空中，面積S，電極間距離x)を想定しています．

＞コンデンサに蓄えられるエネルギーの変化だけでなく，発生するジュール熱も含めて考える必要があります．

とすると保存力的な考えでは駄目なのでしょうかね？純粋に力学的な力による仕事と，それに従う電荷移動が電源を通る分に分けようと思ったのですが．抵抗成分は無視しようと思っていました．

●追加

本当は，2枚の電極の運動方程式と連立して解くのが良いのでしょうが，重力のような中心力のポテンシャルを導入するときに，簡便のために，「準静的」な仕事の積分をしたと類似で計算すれば，ジュール熱に目を瞑る事が出来るようにも感じますが．

Re: エネルギーと力（電磁気学）

yama さんのレス (2007/07/14(Sat) 23:55)

ジュール熱は考えなくてもいいようですね．極板間の力と釣り合う外力を加えるとして，外力のする仕事と電源のする仕事の和がコンデンサのエネルギーの変化に等しいと考えればいいと思います．

電荷 (C'-C)V が電位差Vの区間を移動するので，その積が電源のする仕事になります．極板を引き離すときはこの仕事は負になるので，電源が仕事をされることになります．たとえば電池が充電されたりするのだと思います．

Re: エネルギーと力（電磁気学）

zoro さんのレス (2007/07/15(Sun) 11:18)

tip★さん，

私は，早とちりして，平行板コンデンサを引き離す力を出す問題とばかり思っていました．仕事の計算だとは気づきませんでした．

仕事については，yamaさんのご説明でお分かりともいます．私は静電エネルギとの関係で引っかかっています．

若し宜しければ，tip★さんの計算で，困った点を書けば，静電場の幾何学的理解が得意な方からの解説が得られるかも知れません．

Re: エネルギーと力（電磁気学）

tip★ さんのレス (2007/07/15(Sun) 12:22)

yamaさん，zoroさん，ありがとうございます．

>>電荷 (C'-C)V が電位差Vの区間を移動するので，その積が電源のする仕事になります．

電源のする仕事はどのように定義されているのでしょうか？

Re: エネルギーと力（電磁気学）

yama さんのレス (2007/07/15(Sun) 13:48)

一方の極板から他方の極板に電荷を移動させる仕事が，電源のする仕事だと思います．これに対して，極板自体を動かす（引き離す）仕事が外力のする仕事だと思います．

Re: エネルギーと力（電磁気学）

zoro さんのレス (2007/07/16(Mon) 05:14)

tip★さん，

漸く状況を把握出来て来たと思いますが，それから逆に推定すると，このご質問は，大きな問題の一部ではないかと思うようになりました．

若し宜しければ，完全な質問をお教え下さいませんか．そして，そのどこの部分で納得いかないかをお示し下されば，説明出来る様な気がします．

Re: エネルギーと力（電磁気学）

tip★ さんのレス (2007/07/16(Mon) 09:00)

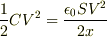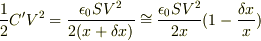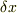コンデンサに蓄えられるエネルギーは変化前： $\frac{1}{2}CV^2=\frac{\epsilon_{0}SV^2}{2x}$ 変化後：： $\frac{1}{2}C'V^2=\frac{\epsilon_{0}SV^2}{2(x+\delta x)} \cong \frac{\epsilon_0SV^2}{2x}(1-\frac{\delta x}{x})$ 変位 $\delta x$ は，非常に小さいとする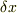． $\delta x$ なる変位をコンデンサに与えると静電容量は減少し，蓄えられ手いる電荷も減少する．この電荷は電源に戻るのであり，このことによるエネルギーの変化を考える必要がある．

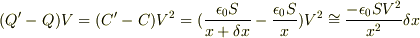
変位により外部から入ったエネルギーは $(Q'-Q)V=(C'-C)V^2=(\frac{\epsilon_0S}{x+\delta x}-\frac{\epsilon_0S}{x})V^2 \cong \frac{-\epsilon_0SV^2}{x^2}\delta x$

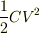この部分を上に書いてあるように， $\frac{1}{2}$ をかけてしまいました．というよりも，静電エネルギーは $\frac{1}{2}CV^2$ なのでこのような間違いになってしまったと考えています．

Re: エネルギーと力（電磁気学）

zoro さんのレス (2007/07/16(Mon) 12:46)

なるほど，考えるべき部品は出ている訳です．問題は，これらをどのように調理するかどうかです．状況を見易くする為に絵にしてみましょう．

●コンデンサの見直し● <pre> 図1コンデンサの配置

`+V`	┌──────────┐0

┌──┤Power supply:emf=V ├────┬─（接地） │└──────────┘ │ 電線│ │電線 │+Q(x） │-Q(x) ┏┷┓┏┷┓ ┃┃+ -┃┃ ┃┃+-┃┃ ┃┃+-┃┃

┃┃+─────────→-┃┃

┃┃+電場の大きさE(x) -┃┃ ┃┃+-┃┃ ┃┃+-┃┃ ┃┃+-┃┃ ┃┃+-┃┃ ┗━┛┗━┛ ｜｜｜｜原点０・ーーーーーーーーーーーーーーー→｜位置x </pre>

此れが普通の平行板コンデンサです．論議を簡単にする為に，電源の負側出力は接地してある事にします．また電極は力学的には十分に柔軟で電極の動きに抵抗する事無く追従するとします．なお，電極構造を保持する機械的な構造は省いています．

コンデンサについてのパラメータには,静電荷の方程式から；

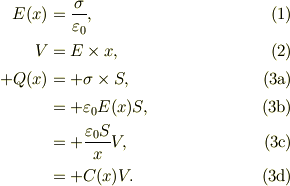
$E(x) &= \frac{\sigma}{\varepsilon_0}, \tag{1}\\V &= E\times x, \tag{2}\\+Q(x) &= +\sigma \times S, \tag{3a}\\&= +\varepsilon_0E(x)S, \tag{3b}\\&= +\frac{\varepsilon_0 S}{x}V, \tag{3c}\\&= +C(x)V. \tag{3d}$

ここで，静電容量，

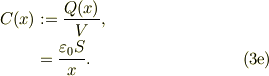
$C(x) &:= \frac{Q(x)}{V}, \\&= \frac{\varepsilon_0 S}{x}. \tag{3e}$

後の便利の為に，静電容量の微分も計算しておきますと；

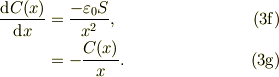
$\frac{\mbox{d}C(x)}{\mbox{d} x} &= \frac{-\varepsilon_{0}S}{x^2},\tag{3f}\\&= -\frac{C(x)}{x}. \tag{3g}$

始めにコンデンサに電荷が無い状態から，電源の電圧をすこしずつあげて，いわゆる準静的に電荷を電極に注入するときに，電極に発生する電位が作りだすエネルギとして静電エネルギが生じます；

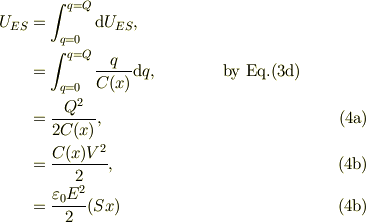
$U_{ES} &= \int_{q=0}^{q=Q}\mbox{d}U_{ES}, \\ &=\int_{q=0}^{q=Q}\frac{q}{C(x)}\mbox{d}q, &\text{by Eq.(3d)}\\ &=\frac{Q^2}{2C(x)}, \tag{4a}\\&=\frac{C(x)V^2}{2}, \tag{4b}\\&=\frac{\varepsilon_0 E^2}{2}(Sx) \tag{4b}$

●コンデンサを外力によって引き離す●

<pre> 図2コンデンサに外力が加わり，引き延ばされる時．

電荷量の移動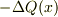：「 $-\Delta Q(x)$ 」 $\ \to \ \to$

`+V`	┌──────────┐0 ↓電線は幾らでも伸びる

┌──┤Power supply:emf=V ├──────────┬─（接地） │└──────────┘ │ 電線│ │電線 │+Q(x+Δx) │-Q(x+Δx) ┏┷┓ ┏┷┓ ┃┃+ -┃┃ ┃┃+-┃┃ ┃┃+-┃┃

┃┃+─────────→-┃┃

┃┃+電場の大きさ E(x+Δx) -┃┃伸ばす力 ┃┃+-┃┃F ┃┃+-┃┃→ ┃┃+-┃┃ ┃┃+-┃┃ ┗━┛┗━┛ ｜｜｜｜｜｜原点０・ーーーーーーーーーーーーーーー→｜位置 x｜ ↑を固定｜ーーーー→｜位置 x+Δx </pre>

＃対向する電極間には正・負の電荷があるので，引力が働いている．＃電磁気を勉強し始めてから，半年ほどの間は，電極間にでる引力は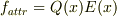，＃ $f_{attr} = Q(x)E(x)$ ＃と思い込んでしました．電磁運動量の論議で，どうやら間違いらしい事に気づいたものの，今回のご質問まで忘れていました．

さて，問題は，電極に電源を繋げたまま(電極間電位差＝一定＝V)にして，電極に外力を掛けて，ゆっくりと広げる場合を考えよと思います．

いま，原点Oの位置(+Qの位置;x=0)を固定して，対向の電極(-Qの電極，位置;x)に図示したように外力Fを加えて，準静的に「x+Δx」まで動かした場合を考えます．

引き離す方向なので，

$\Delta x > 0, \tag{5}$

です．

この力により，コンデンサ系に加わる力学的微量仕事は，

$\Delta W = F\Delta x > 0. \tag{6}$

この変位に伴い，印可起電力Vが一定でも，式(3d)により電荷量に変化が生じる，

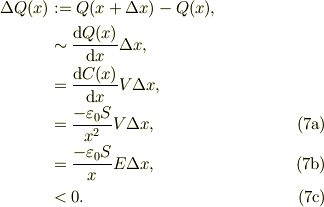
$\Delta Q(x) &:= Q(x+\Delta x) - Q(x),\\&\sim \frac{\mbox{d}Q(x)}{\mbox{d} x}\Delta x,\\&= \frac{\mbox{d}C(x)}{\mbox{d} x}V\Delta x,\\&= \frac{-\varepsilon_{0}S}{x^2}V\Delta x, \tag{7a}\\&= \frac{-\varepsilon_{0}S}{x}E\Delta x, \tag{7b}\\&< 0. \tag{7c}$

これは，外力により間隔xがΔxの分，開いたので，静電容量C(x)が減少した結果，電荷も減少した訳です．

見方を変えれば，正電極では；

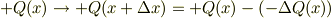
$+Q(x) \to +Q(x+\Delta x) = +Q(x) -\left(-\Delta Q(x)\right)$

の電荷量 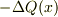$-\Delta Q(x)$ が電源に向けて流失し，同様に負電極では；

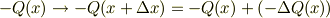
$-Q(x) \to -Q(x+\Delta x) = -Q(x) +\left(-\Delta Q(x)\right)$

と電源から電荷量 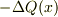$-\Delta Q(x)$ が流入する．

従って，コンデンサから電位差Vを跨いで，電荷移動に伴って失うエネルギ損失は；

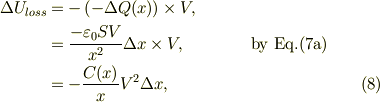
$\Delta U_{loss} &= -\left(-\Delta Q(x) \right)\times V, \\&= \frac{-\varepsilon_{0}SV}{x^2}\Delta x\times V, & \text{by Eq.(7a)}\\&=-\frac{C(x)}{x}V^2 \Delta x,\tag{8}$

となる．

上記の2つのエネルギ変化によって，コンデンサのもつ静電エネルギに加わるのだから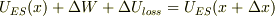， $U_{ES}(x) + \Delta W + \Delta U_{loss} = U_{ES}(x +\Delta x)$ となり，整理すれば；

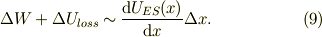
$\Delta W + \Delta U_{loss} \sim \frac{\mbox{d}U_{ES}(x)}{\mbox{d} x}\Delta x. \tag{9}$

電源電圧一定でのコンデンサのもつ静電エネルギを考えるには，式(4b)を用いて容易に計算出来て；

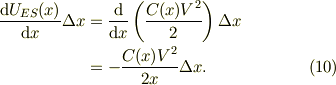
$\frac{\mbox{d}U_{ES}(x)}{\mbox{d} x}\Delta x &= \frac{\mbox{d}}{\mbox{d} x}\left( \frac{C(x)V^2}{2} \right) \Delta x\\&= -\frac{C(x)V^2}{2x} \Delta x. \tag{10}$

最終的に，式(6),(8),(10)を式(9)の全エネルギ保存の式に代入すうると；

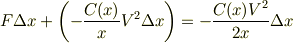
$F\Delta x + \left( -\frac{C(x)}{x}V^2 \Delta x \right) = -\frac{C(x)V^2}{2x} \Delta x$

整理して，微小変位を払うと；

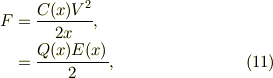
$F &= \frac{C(x)V^2}{2x}, \\&= \frac{Q(x)E(x)}{2}, \tag{11}$

と言った，応力テンソルで示されるのと同様に，1/2のファクタが付いていますね．

Re: エネルギーと力（電磁気学）

tip★ さんのレス (2007/07/16(Mon) 17:14)

zoroさん，丁寧な解説ありがとうございます．

近似計算のところでテイラー展開を使っているところはすごいなぁと思いました．参考にしたいと思います．

コンデンサから電位差Vを跨いで，電荷移動に伴って失うエネルギ損失がなぜ (８)のような式になるのかイメージがわきません．どのように考えればいいでしょうか？

Re: エネルギーと力（電磁気学）

zoro さんのレス (2007/07/16(Mon) 17:50)

＞コンデンサから電位差Vを跨いで，電荷移動に伴って失うエネルギ損失がなぜ＞(８)のような式になるのかイメージがわきません．

すこし戻って，通常の静電エネルギを求める所を考えます．

〜〜〜自己引用：初め〜〜〜〜始めにコンデンサに電荷が無い状態から，電源の電圧をすこしずつあげて，いわゆる準静的に電荷を電極に注入するときに，電極に発生する電位が作りだすエネルギとして静電エネルギが生じます；

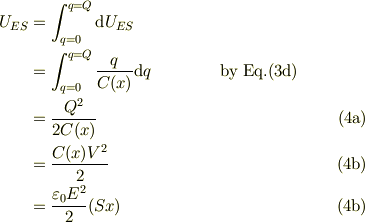
$U_{ES} &= \int_{q=0}^{q=Q}\mbox{d}U_{ES} \\ &=\int_{q=0}^{q=Q}\frac{q}{C(x)}\mbox{d}q &\text{by Eq.(3d)}\\ &=\frac{Q^2}{2C(x)} \tag{4a}\\ &=\frac{C(x)V^2}{2} \tag{4b}\\ &=\frac{\varepsilon_0 E^2}{2}(Sx)\tag{4b}$

〜〜〜自己引用：終り〜〜〜〜

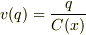この場合でしたら，電源が負電極から $\mbox{d}q$ の電荷を引き抜き，電位差 $v(q)=\frac{q}{C(x)}$ を跨いで持ち上げて，正電極に 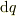$\mbox{d}q$ に注入する，と考えられませんか．

今回の問題は，一定電圧差を跨いで，電極電荷が逆戻る過程なので，静電エネルギは減少します．

式の算法の話です．今回のようにあまり計算慣れの無い場合，・微量変化による変化方向の確認．・式の検算を考えると，一度，関数として定義しておく方が，やり易いようです．

おそらく，プログラムでもメインでは，全体の関係を記述し，関数やサブルーチンに具体的な処理を書いて置くとデバックが楽になるからです．

〜〜〜勿論，日常的に良く知っている問題は端折って表現しますが...．

Re: エネルギーと力（電磁気学）

tip★ さんのレス (2007/07/16(Mon) 18:19)

zoroさん，ありがとうございます．

関数を図に描くとわかりやすいですね．

始めにコンデンサに電荷が無い状態から，電源の電圧をすこしずつあげて，いわゆる準静的に電荷を電極に注入するときに，電極に発生する電位が作りだすエネルギとして静電エネルギーの場合は 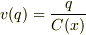$v(q)=\frac{q}{C(x)}$ なので，これを描くと一次関数でこの関数とv(q)=0とq=Q（Q=CV）を囲む面積が静電エネルギーで，

今回の問題の場合はVが一定なので，長方形の面積を求めればよいことになると思うんですがどうでしょう？

Re: エネルギーと力（電磁気学）

zoro さんのレス (2007/07/16(Mon) 18:44)

＞今回の問題の場合はVが一定なので，長方形の面積を求めればよいことになると思うんですがどうでしょう？

正に仰る通りなので，

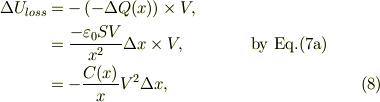
$\Delta U_{loss} &= -\left(-\Delta Q(x) \right)\times V, \\ &= \frac{-\varepsilon_{0}SV}{x^2}\Delta x\times V, & \text{by Eq.(7a)}\\ &=-\frac{C(x)}{x}V^2 \Delta x,\tag{8}$

としています．

右辺の最上段は； (一定の電位差V)*(通過する微小電荷) という意味で，微小「長方形面積」に対応します．

微分の式から微分方程式を求めるのに慣れて来ると，電磁気の基礎方程式からケース・バイ・ケースで必要な関係式を出せる訳です．例えば，式(9)で；

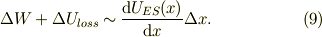
$\Delta W + \Delta U_{loss} \sim \frac{\mbox{d}U_{ES}(x)}{\mbox{d} x}\Delta x. \tag{9}$

直接微少量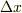， $\Delta x$ を払い，極限操作をすれば，

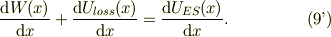
$\frac{\mbox{d} W(x)}{\mbox{d} x} + \frac{\mbox{d} U_{loss}(x)}{\mbox{d} x} = \frac{\mbox{d}U_{ES}(x)}{\mbox{d} x}. \tag{9'}$

と微分方程式に化けます．

いま，式(6)から式(9')の左辺の第一項は引き離す力Fですが，この力は電極間が引き合う力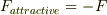， $F_{attractive}=-F$ と方向が逆ですから，

$F_{attractive} &=-F\\&= -\frac{\mbox{d} W(x)}{\mbox{d} x}\\&= -\left( \frac{\mbox{d}U_{ES}(x)}{\mbox{d} x} -\frac{\mbox{d} U_{loss}(x)}{\mbox{d} x} \right)\\&= -\frac{\mbox{d}}{\mbox{d} x} \left[ U_{ES}(x)-U_{loss}(x) \right]$

と変形出来ます．ここらの解釈をどうするかを考えて下さるのも面白いかも知れません．

Re: エネルギーと力（電磁気学）

tip★ さんのレス (2007/07/16(Mon) 23:38)

>>ここらの解釈をどうするかを考えて下さるのも面白いかも知れません．

物理的な意味で言うと，エネルギー変化を妨げるほうに力が働く，ような感じですか？

つまり， $U_{ES}(x)-U_{loss}(x)$ は負であり，エネルギーは減少するので，力はエネルギーが増加する方向に力が働きます．今回は，極板間隔を大きくしたためエネルギーが減少したので，極板間隔を小さくすれば，エネルギーが増加すると考えられるので，極板間隔を小さくする方向のちから，つまり，吸引力が働く．

Re: エネルギーと力（電磁気学）

zoro さんのレス (2007/07/17(Tue) 00:34)

力学で言う所のポテンシャル・エネルギと同じ振る舞いだろうと思います．

例えば，電源を切り話して，電極電荷一定で計算するとしても，その引力はおなじになります．逆に言えば，その場合でもポテンシャル・エネルギは同じです．

詳しい事は，解析力学で一般論を学ぶ時まで，お待ち下さいね．

Re: エネルギーと力（電磁気学）

tip★ さんのレス (2007/07/17(Tue) 00:42)

うちの大学は解析力学はカリキュラムの中に入ってないんですよねぇ・・・いつか独学でがんばってみようと思います．

[home] [掲示板] [ページの先頭]