テンソル
テンソル
kenta さんの書込 (2007/07/13(Fri) 17:44)
はじめましてkentaといいます. 分からないことがあります.教えていただけたら幸いです.
Tνμ を二階共変テンソル(の成分),U^ν,U^μを(反変ベクトル(の成分)としたとき,TνμU^νU^μがスカラーとなることがわからないのですが・・・ Tν'μ'U^ν'U^μ'=TνμU^νU^μ
どう,導き出せばいいのでしょうか.^は上付きです.
よろしくお願いします.
Re: テンソル
tonda さんのレス (2007/07/24(Tue) 15:26)
返信が遅れてすみません.
共変ベクトル成分であるための条件は,基底ベクトルと同一の変換式に従うベクトルであること. 反変ベクトル成分であるための条件は,添字の上下を逆転させた変換に従うベクトル.
とは違うのでしょうか・・・??
Re: テンソル
toorisugari no Hiro さんのレス (2007/07/24(Tue) 16:14)
> 共変ベクトル成分であるための条件は,基底ベクトルと同一の変換式に従うベクトルであること. > 反変ベクトル成分であるための条件は,添字の上下を逆転させた変換に従うベクトル.
それを式で表現すればよいわけです.
正確には(3次元ユークリッド空間で考えると),曲線座標系 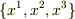 に対して,ベクトル
に対して,ベクトル 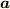 の
反変ベクトル成分
の
反変ベクトル成分 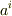 は基底を
は基底を
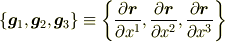
でとった成分( 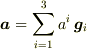 ),
共変ベクトル成分
),
共変ベクトル成分 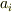 は基底を
は基底を
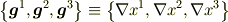
でとった成分( 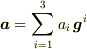 ),
であり(直角座標系では
),
であり(直角座標系では 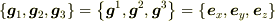 なので,成分は同一です),座標変換
なので,成分は同一です),座標変換
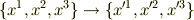
に対して,ベクトル 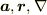 は変化しないが基底が変化する事から,各成分の変換則が導き出されます.(偏微分の鎖則の練習問題ですね.)
は変化しないが基底が変化する事から,各成分の変換則が導き出されます.(偏微分の鎖則の練習問題ですね.)
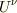 が反変ベクトル成分であるための条件は何ですか?
が反変ベクトル成分であるための条件は何ですか?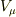 が共変ベクトル成分であるための条件は何ですか?
が共変ベクトル成分であるための条件は何ですか?