ベクトル公式
ベクトル公式
けん(大学2年) さんの書込 (2007/07/13(Fri) 10:58)
a,b,cを3次元ベクトルとします.
ax(bxc)=b(a・c)-(a・b)c でa,bを∇で置き換えると正しい公式が得られます.(∇が項の最後にならないように作為的に内積の順番を入れ替えます.) しかし, c・(axb)=b・(cxa) でcを∇で置き換えると誤った式が出てきてしまいます.この公式から, ∇・(axb)=b・(∇xa)-a・(∇xb) を導くことはできないのでしょうか.
それから, h/(2π)を意味する,hの上に線のあるものは何と読むのが一般的なのでしょうか.クロストエイチ,エイチバー,エイチスラッシュなどいろいろな人がいますが.
以上よろしくおねがいします.
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/07/13(Fri) 12:40)
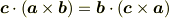
となるが,
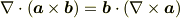
でなく

を導くにはどうすればいいかということですね.
これは「積の微分則」(ライプニッツ則)を考慮すれば良いです.
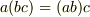 ですが,
ですが, 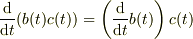 ではないですね.
ではないですね.
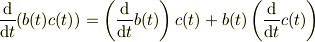
ですね.
おなじようにベクトル微分演算子 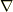 にもライプニッツ則が適用されなければいけません.
にもライプニッツ則が適用されなければいけません.
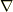 が微分として関数
が微分として関数  に作用しているのを
に作用しているのを 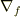 と表現すれば,
と表現すれば, 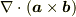 の微分は
の微分は 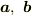 それぞれに作用するので,
それぞれに作用するので,
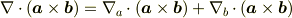
とおくのがライプニッツ則です. (先ほどの計算ではライプニッツ則を
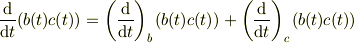
と表現して,あとは 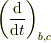 をただの数と考え,結合則と交換則を使えば先ほどとおなじ結果が出ますね.)
をただの数と考え,結合則と交換則を使えば先ほどとおなじ結果が出ますね.)
 を普通のベクトルとみなして,ベクトル計算をし,結合しているペアを近くに持ってくればいいです.
を普通のベクトルとみなして,ベクトル計算をし,結合しているペアを近くに持ってくればいいです.
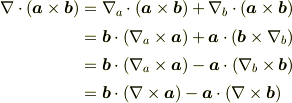
# 本当は  とするより,微分相手を→でつないだ方が汎用性があるのですが,TeXでは表現できないので,こうしています.
とするより,微分相手を→でつないだ方が汎用性があるのですが,TeXでは表現できないので,こうしています.
# 一般には添え字計算するのが主流だと思いますが,これでやった方が早い場合が多いので,使い分けています.
Re: ベクトル公式
zoro さんのレス (2007/07/14(Sat) 00:28)
ナイーブな外積公式;
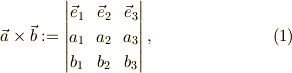
を用いる方法を示します.泥臭い計算では在りますが,どうしても公式を忘れた様な場合に,有用です.
求めるべき式, 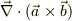 は,上の公式を用いれば,
は,上の公式を用いれば,
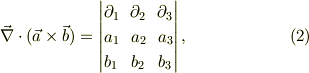
この内, 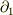 の成分に着目すると,
の成分に着目すると,
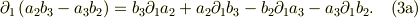
残りの2成分も,上式の(1,2,3)を隣環(漢字が可笑しい?)の順に換えた,(2,3,1)と(3,1,2)として,加え合わせれば良い.
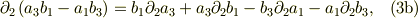
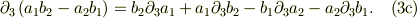
式(3a,b,c)の右辺の和において,bの係数は,aの偏微分だけで,しかも 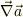 の成分に等しい.同様なことが,aの係数にも成立.
の成分に等しい.同様なことが,aの係数にも成立.
以下,省略.
Re: ベクトル公式
Joh さんのレス (2007/07/14(Sat) 02:36)
▽は微分演算子なので,「右から来る物を微分してしまう」という機能があります.
A▽は,(Aがスカラーにせよ,ベクトルにせよ)依然として右から掛かってくる物を微分してしまう作用を持った演算子です.しかし,▽Aは『Aの微分』であって,意味が全然違います.
確かに▽はベクトルですので,『ベクトルの公式が使えるのではないか』というけんさんの疑問はもっともですが,演算子は右から掛かってくる物に作用するということを忘れてはいけません.(a,b,cだけの公式の導出では,どこかでab=baを使って簡単化している場所があると思いますので探してみてください.)
Re: ベクトル公式
けん(大学2年) さんのレス (2007/07/27(Fri) 11:59)
遅くなってすみません.
> toorisugari no Hiroさん 解説ありがとうございます.計算途中で∇bが最後に来ているところがありますが,微分演算子を普通のベクトルとみなしてもいいのですか? それから,微分相手を→でつなぐとは,∇からベクトルに式の上に曲線の矢印を引くということですか?(a+b)(c+d)を初めて計算するときのように.
>zoroさん 外積公式を使うこともできるんですね.参考になりました.ありがとうございました.
>Johさん c(ab)=c(ab)を使っている箇所を発見できました.ご指摘ありがとうございます.
Re: ベクトル公式
zoro さんのレス (2007/07/31(Tue) 22:24)
>h/(2π)を意味する,hの上に線のあるものは何と読むのが一般的なのでしょうか.
私の若い頃は,エイチ・バーと呼んでいました.うろ覚えですが,エイチ・カットという言い方もあったように思います.
このLaTeXでも「 hbar 」と書くと, 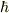 ですね.
ですね.
ちなみに,英辞郎では「h-bar」で出ており,「《物理》h バー」と書いてあります.
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/07/31(Tue) 23:05)
> 計算途中で∇bが最後に来ているところがありますが,微分演算子を普通のベクトルとみなしてもいいのですか?
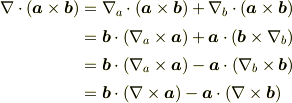
の2行目の事ですか? 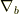 は
は 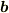 にのみ(微分)作用することがわかっていますから,通常のベクトル微分演算子と違って,順番や作用する範囲を気にせず,ただのベクトルとして考えていいです.つまり,
にのみ(微分)作用することがわかっていますから,通常のベクトル微分演算子と違って,順番や作用する範囲を気にせず,ただのベクトルとして考えていいです.つまり,
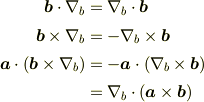
が成り立ちます.
> それから,微分相手を→でつなぐとは,∇からベクトルに式の上に曲線の矢印を引くということですか?(a+b)(c+d)を初めて計算するときのように.
そうです.
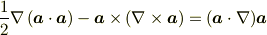
の証明は 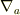 の方法では破綻しますので,矢印法でないと苦しいです.
(右辺の
の方法では破綻しますので,矢印法でないと苦しいです.
(右辺の 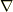 は右側の
は右側の 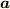 にのみ作用します.従来の表記もここら辺苦しいですね.)
ま,混乱がなければ,数字などの下付添え字で区別してもいいのですが.
にのみ作用します.従来の表記もここら辺苦しいですね.)
ま,混乱がなければ,数字などの下付添え字で区別してもいいのですが.
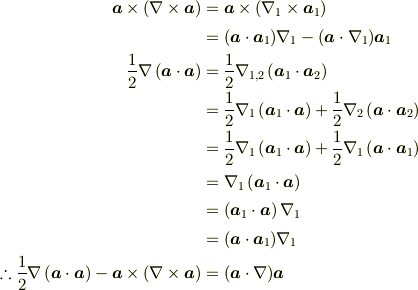
(少し,冗長に計算しました.慣れれば4,5行で計算できます.)
Re: ベクトル公式
けん(大学2年) さんのレス (2007/08/02(Thu) 18:42)
>zoroさん 英辞郎がエイチバーならエイチバーが多いんでしょうね.ありがとうございました.
>toorisugari no Hiroさん 8行目の b・∇b=∇b・b ですが,この∇bはそれよりも前にあるbにも作用すると定義されているのですか?
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/08/02(Thu) 20:14)
見づらいので,そろそろ,TeXを使ってみてはどうですか?
> b・∇b=∇b・b > ですが,この∇bはそれよりも前にあるbにも作用すると定義されているのですか?
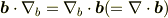
において, 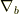 は
は 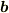 に微分作用しています.(順番は関係ないです.)
に微分作用しています.(順番は関係ないです.)
式の一部として考えるときには,別のベクトルに微分作用している場合も同様に考えられます.
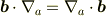
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/08/02(Thu) 21:45)
> # 本当は 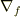 とするより,微分相手を→でつないだ方が汎用性があるのですが,TeXでは表現できないので,こうしています.
とするより,微分相手を→でつないだ方が汎用性があるのですが,TeXでは表現できないので,こうしています.
今井さんの流体力学(前編)
の69ページにある記法風にやってみようとstackrelで試してみました.
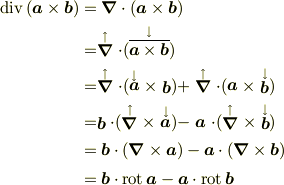
2行目は2本の矢印で結びたいのだけど,ま,なんとか通じるかな.....ラプラシアンは大変そうだけど....
Re: ベクトル公式
zoro さんのレス (2007/08/03(Fri) 02:22)
>ま,なんとか通じるかな.
感じは出て来てますね.ならば,
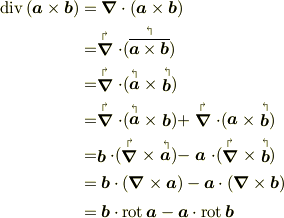
とするのは如何でしょうか?
・ちょっと「結合対」が視認しやすいのと,記述が短いかも.
・ある種のルール;
「 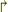 」と「
」と「 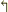 」との間に「左括弧の類」が無くなったら,それらを消去して良い.
」との間に「左括弧の類」が無くなったら,それらを消去して良い.
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/08/03(Fri) 10:18)
zoroさんありがとうございます.Lsh,Rshですか,なるほど.下向きがあれば最高なのですがね.
Re: ベクトル公式
zoro さんのレス (2007/08/03(Fri) 14:10)
toorisugari no Hiroさん,LaTeXにも手書きに勝てない事があって,ちょっと嬉しかったりしますね.
Re: ベクトル公式
けん(大学2年) さんのレス (2007/08/03(Fri) 14:37)
toorisugari no Hiroさん,zoroさん,その演算子も矢印もよく分かりました.ありがとうございました. TEXは少し勉強してみたんですが,何しろパソコン苦手で,難しく,苦労しています.
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/08/04(Sat) 00:17)
> TEXは少し勉強してみたんですが,何しろパソコン苦手で,難しく,苦労しています.
期待しています.がんばってくださいね.
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/08/04(Sat) 00:20)
> LaTeXにも手書きに勝てない事があって,ちょっと嬉しかったりしますね.
free hand系は圧倒的にTeXは不得手ですよね.
そういう意味では完全反対称テンソル 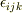 を使った添え字計算がTeXには向いていますね.
を使った添え字計算がTeXには向いていますね.
Re: ベクトル公式
zoro さんのレス (2007/08/04(Sat) 14:16)
>free hand系は圧倒的にTeXは不得手ですよね.
「SVG+LaTeX」の組み合わせの価値は,それなりにあるという事ですかね.
Re: ベクトル公式
toorisugari no Hiro さんのレス (2007/08/04(Sat) 16:06)
> 「SVG+LaTeX」の組み合わせの価値は,それなりにあるという事ですかね.
SVGはよく知らないですがXML形式の複合画像フォーマットてな理解でいいですかね?
ま,そこまでいかなくても,dviをpostscriptファイルにして,Illustlatorあたりで加工すれば,画像として「矢印つきの計算式」はできます.が,もうTeXからは直接編集や管理はできないですよね.
あるいは,powerpointでプレゼンする場合なら,TeXpointを使えば,やりたいことはできそうですし,fileを一元管理できますね.(有料になってからは使っていない...)
TeXのpic環境と融合するようなうまい方法があればいいのですが.
Re: ベクトル公式
zoro さんのレス (2007/08/04(Sat) 21:17)
>SVGはよく知らないですがXML形式の複合画像フォーマットてな理解でいいですかね?
と思います.MathMLが数式を表現するマークアップ言語(ML)であるのに対して,Scalable Vector Graphics(SVG)はヴェクタ型のグラフィックスを表現するマークアップ言語(ML)です.ブラウザに依存性が高いですが,最近のFirefoxではかなりの表示性能を誇ります.「かなり」というのが残念な所です.
そもそも「MathML」が「TeX」だったらと思うのは私だけではないと思うのですが.一種の歴史的な捻れ現象でしょう.
>dviをpostscriptファイルにして,Illustlatorあたりで加工すれば,画像として「矢印つきの計算式」はできます.
Illustlatorキラーと呼ばれるInkscapeでは,下記のようなトライアルもあるようです.
・Inkscape de LaTeX
画像処理形の数式や画像は,視力が悪い者に取っては,小さすぎて見にくく,ズームしても見難いのです.かといってpdfは,気楽にノート作りには使えないとおもいます.