伝導電子濃度nの導出(半導体工学)(続)
伝導電子濃度nの導出(半導体工学)(続)
tip★ さんの書込 (2007/07/12(Thu) 16:39)
まずは,お詫びをさせてください. 前のスレッドでは自分のレベルでは到底理解できるレベルではないと思い,削除させていただきました.今思うと削除する必要はなかったと後悔しています.削除するにしても一度断りを入れておくべきでした. 本当にすみませんでした.
今日,半導体工学の本で,キャリア濃度の温度依存性のセクションを読んでいるうちにやっと篠原さんのおっしゃっている意味が分かりました. サーミスタが真性半導体であれば,活性化エネルギーはエネルギーギャップの2分の1に相当する. しかし,不純物半導体は,真性領域,出払い領域,不純物領域の三つの領域があり,高温であれば,不純物半導体は真性領域にあり,真性半導体とみなせるので,活性化エネルギーはエネルギーギャップの2分の1になり,一方,低温であれば,価電子帯から伝導帯に励起される電子がほぼないとみなせて,伝導電子濃度がドナーから励起された電子の数で決まるので,活性化エネルギーは伝導帯底からのドナー準位の深さに相当する. ということですよね?
あともうひとつ相当するものがあったような気がしますが,それはちょっと分かりませんでした.というより思い出せませんでした.
上のことから,実験で求めた活性化エネルギーは高温付近(室温)のものであるので,活性化エネルギーはエネルギーギャップの2分の1に相当する.
この解釈であってますか?
もう1つ質問です.
n形半導体のキャリア濃度の温度依存性で,温度が高く,ドナーが全てイオン化している場合,ドナー濃度を 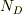 とすれば,
電気的中性条件から
とすれば,
電気的中性条件から
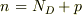
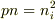 なので,
なので,
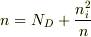 したがって,
したがって,
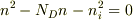 これを解くと
これを解くと
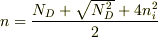 となります.(√の長さを調整できませんでした.)
これはただ計算するだけなので問題ないのですが,
友達が直感的に電子の濃度を求めると
となります.(√の長さを調整できませんでした.)
これはただ計算するだけなので問題ないのですが,
友達が直感的に電子の濃度を求めると
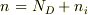 にならない?
と質問してきました.
言われてみればそんな感じもするなぁと思い自分はこの質問に反論できませんでした.
この式にはどんな欠陥があるのでしょうか?
にならない?
と質問してきました.
言われてみればそんな感じもするなぁと思い自分はこの質問に反論できませんでした.
この式にはどんな欠陥があるのでしょうか?
Re: 伝導電子濃度nの導出(半導体工学)(続)
zoro さんのレス (2007/07/13(Fri) 18:41)
>みなさん,怒ってるみたいですね
そうではないと思います.少なくとも,前半の問題に関しては,篠原さんとの論議を見守ってられると思います.
後半の論議は,私には理解出来ないだけです.むしろ前半の問題がクリアしてから論議した方が解り易いように思えました,ので,コメントを差し控えています.
Re: 伝導電子濃度nの導出(半導体工学)(続)
篠原 さんのレス (2007/07/13(Fri) 20:25)
「みなさん,怒ってるみたいですね・・・(汗)」
いえ,そんなことないと思いますが・・・
まず,前半部分について.
「不純物半導体は,真性領域,出払い領域,不純物領域の三つの領域があり,高温であれば,不純物半導体は真性領域にあり,真性半導体とみなせるので,活性化エネルギーはエネルギーギャップの2分の1になり,一方,低温であれば,価電子帯から伝導帯に励起される電子がほぼないとみなせて,伝導電子濃度がドナーから励起された電子の数で決まるので,活性化エネルギーは伝導帯底からのドナー準位の深さに相当する.」
短期間によく勉強しましたね.そのとおりです.
「上のことから,実験で求めた活性化エネルギーは高温付近(室温)のものであるので,活性化エネルギーはエネルギーギャップの2分の1に相当する.」
えっと,前回よりだいぶ筋道が立てられるようになってきましたね. 学部生の学生実験のレポートとしては,それなりの考察だと思います. ただ,この文では,なぜ今回測定した温度領域が真性領域といえるのか,根拠がないように思えます. まぁ,私のレポートではないので,ご自身で満足されるのなら,それで提出したらよいと思います.
なお,参考までに,私の意見を書いておくと,一般に使われている多くのサーミスタではバンドによる伝導ではなく,「ホッピング伝導」とよばれる伝導機構だと思います.(別にレポートでまねする必要はないと思います.) 気が向いたときにでも「ホッポング伝導」を調べてみてください.
後半部分について.
まず,質問に答える前に,補足をしておきます.
n形半導体について,電荷中性の条件よりキャリア密度はドナー密度を 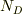 として,
として,
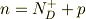
ここで, 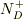 はイオン化ドナー密度で,ドナー準位が十分に浅い場合にはドナーのほとんどがイオン化しているので,
はイオン化ドナー密度で,ドナー準位が十分に浅い場合にはドナーのほとんどがイオン化しているので, 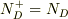 となるため,tip★さんの示した式になります.
ここで,
となるため,tip★さんの示した式になります.
ここで, 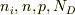 について数の比較をして見ましょう.シリコンを前提とします.
まず
について数の比較をして見ましょう.シリコンを前提とします.
まず 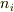 は,
は, 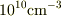 程度です.
これに対し,一般にドナー
程度です.
これに対し,一般にドナー 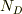 は少なくても
は少なくても 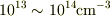 程度の数,ドーピングされます.
(多いときには
程度の数,ドーピングされます.
(多いときには 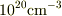 以上ドープされることもあります.)
このような場合,tip★さんの示した式からも分かるとおり,ほとんど
以上ドープされることもあります.)
このような場合,tip★さんの示した式からも分かるとおり,ほとんど 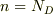 となり,電子密度に比べて真性キャリア密度や正孔密度は何桁も小さな値となることが分かります.
なので,ほとんどの場合,
となり,電子密度に比べて真性キャリア密度や正孔密度は何桁も小さな値となることが分かります.
なので,ほとんどの場合, 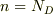 と近似してしまいます.
と近似してしまいます.
さて,質問に戻りましょう.
まず, 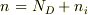 は,
は, 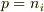 とならない限り,電荷中性の条件を満たしていないことは明らかです.
では,なぜ
とならない限り,電荷中性の条件を満たしていないことは明らかです.
では,なぜ 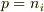 とならないのか.
それは,フェルミ準位の位置が真性半導体とn形半導体では違う位置に来るからです.
当然,正孔密度はフェルミ準位により変化しますよね.
とならないのか.
それは,フェルミ準位の位置が真性半導体とn形半導体では違う位置に来るからです.
当然,正孔密度はフェルミ準位により変化しますよね.
もう少し別の見方をして見ましょう. 今議論している電子や正孔の密度は熱平衡状態であることが前提です. 熱平衡状態は,生成される電子正孔対と消滅する電子正孔対のバランスで決まりますよね. ここで,熱エネルギーによりバンドギャップを飛び越えて生成される電子正孔対の数は,真性半導体でも不純物半導体でも変わらないはずですよね. 一方,消滅する電子正孔対について考えて見ましょう. 電子は,ドナー準位から励起されて出てきた電子も伝導帯にいるわけだから,伝導帯には電子が「うじゃうじゃ」いるわけです. 一方,正孔は熱励起によりバンドギャップを飛び越えたほんのわずかな正孔しかいない状態です.
ここで,正孔の気持ちになって見ましょう. ほんのわずかな確率で熱励起されてできた正孔ですが,よく見たら周りは電子だらけです. せっかく励起されてもすぐに周りの電子に捕まって再結合してしまう正孔が実はほとんどなのです. 一方電子は,熱励起される電子の数よりもはるかに多い電子がドナーから供給されます. このためバンドギャップを乗り越えて電子正孔対ができても,また少ない確率で電子と再結合しても,ほとんど電子の数に影響はありません.
ということで,同じシリコンの中でも,真性半導体と不純物半導体では再結合するキャリアの割合が違う事になります. このため,少数キャリアの数は真性キャリア密度と異なる値になります.
こんな感じですが,ご理解いただけますか?
Re: 伝導電子濃度nの導出(半導体工学)(続)
篠原 さんのレス (2007/07/13(Fri) 22:03)
明日からしばらくネットにつなげられるか分かりません. 返信がなくても,怒っているわけではありませんので・・・. 一応,ご連絡まで.
Re: 伝導電子濃度nの導出(半導体工学)(続)
tip★ さんのレス (2007/07/14(Sat) 12:46)
ヨカッタ〜〜!!
みなさん,ありがとうございます.
>>ただ,この文では,なぜ今回測定した温度領域が真性領域といえるのか,根拠がないように思えます.
そのとおりですね. サーミスタは真性領域で動作させるものだからでしょうか? これでは理由になったないような・・・ もう少し考えてみます.
>>一般に使われている多くのサーミスタではバンドによる伝導ではなく,「ホッピング伝導」とよばれる伝導機構だと思います.
そうなんですか?? 調べてみたいと思います!!
>>ここで, 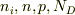 について数の比較をして見ましょう.シリコンを前提とします.
まず
について数の比較をして見ましょう.シリコンを前提とします.
まず 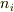 は,
は, 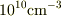 程度です.
これに対し,一般にドナー
程度です.
これに対し,一般にドナー 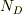 は少なくても
は少なくても 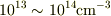 程度の数,ドーピングされます.
このような場合,tip★さんの示した式からも分かるとおり,ほとんど
程度の数,ドーピングされます.
このような場合,tip★さんの示した式からも分かるとおり,ほとんど 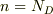 となり,電子密度に比べて真性キャリア密度や正孔密度は何桁も小さな値となることが分かります.
なので,ほとんどの場合,と
となり,電子密度に比べて真性キャリア密度や正孔密度は何桁も小さな値となることが分かります.
なので,ほとんどの場合,と 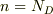 近似してしまいます.
近似してしまいます.
これは,室温の場合で,シリコンなので出払い(飽和)領域の場合ですよね?
>>tip★さんの示した式からも分かるとおり
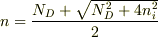 のことですよね?
のことですよね?
>>それは,フェルミ準位の位置が真性半導体とn形半導体では違う位置に来るからです. 当然,正孔密度はフェルミ準位により変化しますよね.
正孔のキャリア密度は 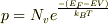 で,n形半導体のフェルミ準位は真性半導体のそれよりも高いところに位置しているので,n形半導体と真性半導体の正孔のキャリア密度は異なり,真性半導体の正孔のキャリア密度は真性キャリア密度
で,n形半導体のフェルミ準位は真性半導体のそれよりも高いところに位置しているので,n形半導体と真性半導体の正孔のキャリア密度は異なり,真性半導体の正孔のキャリア密度は真性キャリア密度 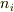 なので,
なので, 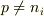 という解釈であってますか?
という解釈であってますか?
>>このためバンドギャップを乗り越えて電子正孔対ができても,また少ない確率で電子と再結合しても,ほとんど電子の数に影響はありません. ということで,同じシリコンの中でも,真性半導体と不純物半導体では再結合するキャリアの割合が違う事になります. このため,少数キャリアの数は真性キャリア密度と異なる値になります.
再結合割合Rは
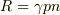
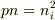 は真性半導体でも不純物半導体でも成り立つので,再結合の割合は同じのような気がします.
は真性半導体でも不純物半導体でも成り立つので,再結合の割合は同じのような気がします.
とりあえず,全体的なイメージとして,
不純物半導体は 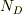 と価電子帯の電子の励起は独立におき,価電子帯の電子は真性半導体と同じように
と価電子帯の電子の励起は独立におき,価電子帯の電子は真性半導体と同じように 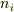 が励起されるが,真性半導体と不純物半導体とでは再結合のメカニズムが異なるから正孔濃度と真性キャリア濃度は異なるという考えであっているでしょうか?
が励起されるが,真性半導体と不純物半導体とでは再結合のメカニズムが異なるから正孔濃度と真性キャリア濃度は異なるという考えであっているでしょうか?
Re: 伝導電子濃度nの導出(半導体工学)(続)
篠原 さんのレス (2007/07/23(Mon) 01:41)
変身が遅くなり,大変申し訳ありません.
> |5d323a592d4297bfc0e3068e20e0868b| は真性半導体でも不純物半導体でも成り立つので,再結合の割合は同じのような気がします.
そのとおりです. 熱平衡状態においては,熱励起されるキャリアと再結合するキャリアがつりあっているので,真性半導体でも不純物半導体でも,熱励起されるキャリアの数が同じであれば,再結合するキャリアの数も同じです.
でも,あくまでもこれは「熱平衡状態」での話です.
では,もともとの疑問の中にあったように, 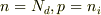 を代入したらどうなりますか?
再結合割合Rは,桁違いに大きくなってしまいます.熱平衡状態より何桁も多いキャリアが再結合して,少数キャリア密度はどんどん減ります.
結局,
を代入したらどうなりますか?
再結合割合Rは,桁違いに大きくなってしまいます.熱平衡状態より何桁も多いキャリアが再結合して,少数キャリア密度はどんどん減ります.
結局, 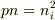 に落ち着くまで,少数キャリア密度が減り続け,熱平衡状態で落ち着くわけです.
このため,不純物半導体では少数キャリア密度が
に落ち着くまで,少数キャリア密度が減り続け,熱平衡状態で落ち着くわけです.
このため,不純物半導体では少数キャリア密度が 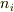 にはならない,という説明で納得いただけますか?
にはならない,という説明で納得いただけますか?
Re: 伝導電子濃度nの導出(半導体工学)(続)
tip★ さんのレス (2007/07/23(Mon) 13:27)
なぜ 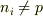 となるのか分かりました.
昨日の夜思いついて,今日書こうと思っていたのですが,まさか今日返信が来るとは思っていなかったので,返信がなかっとという前提で書きたいと思います.
となるのか分かりました.
昨日の夜思いついて,今日書こうと思っていたのですが,まさか今日返信が来るとは思っていなかったので,返信がなかっとという前提で書きたいと思います.
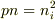 というのは,熱平衡状態であれば,真性半導体でも,不純物半導体でも成り立ちます.つまり,伝導電子と正孔はこれが成り立つように増えていくと考えれます.
というのは,熱平衡状態であれば,真性半導体でも,不純物半導体でも成り立ちます.つまり,伝導電子と正孔はこれが成り立つように増えていくと考えれます.
ここで,まずある温度を設定します. 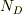 が全てイオン化していて,かつ,あまり温度が高くない場合(
が全てイオン化していて,かつ,あまり温度が高くない場合( 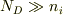 )を考えます.
)を考えます.
また, 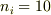 ,
, 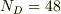 とします.
とします.
(1)真性半導体の場合
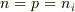 なので,
なので,
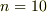 ,
, 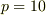 となります.
となります.
(2)不純物半導体(n形)の場合
全てイオン化しているので, 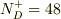 ,
価電子帯から伝導帯に励起する電子の数を
,
価電子帯から伝導帯に励起する電子の数を 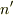 とすると,
とすると,
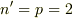 となり,
となり, 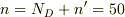 であるので,
であるので, 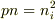 が成り立ちます.
よって,
が成り立ちます.
よって, 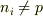 となります.
となります.
つまり,次のことが言えると思います. 不純物半導体の場合は温度が低い場合は,真性キャリア濃度が小さいく,ドナーから励起される電子が多いため,不純物半導体の価電子帯から伝導帯に励起する電子は,真性半導体の価電子帯から伝導帯に励起する電子と比べると,小さいことがわかります. もっと言えば,不純物半導体の場合,飽和領域,不純物領域(温度が低い場合)では,ドナーから励起される電子が邪魔で,真性半導体の同じように価電子帯から伝導帯に励起する電子が増えていってくれない. 価電子帯から伝導帯に励起する電子は少数キャリアである正孔と同じ値なので,正孔も真性半導体の場合のように,増えていってくれない.
篠原さん,これであっていますか?
Re: 伝導電子濃度nの導出(半導体工学)(続)
篠原 さんのレス (2007/07/25(Wed) 10:57)
遅くなりました. すいません.
> 不純物半導体の価電子帯から伝導帯に励起する電子は,真性半導体の価電子帯から伝導帯に励起する電子と比べると,小さいことがわかります.
違うと思います,温度が同じなら,不純物半導体でも,真性半導体でも,価電子帯から伝導帯へ励起される電子の数は同じだと思います. また,熱平衡状態では,熱により励起される電子の数と再結合する電子の数は等しいはずです.
Re: 伝導電子濃度nの導出(半導体工学)(続)
tip★ さんのレス (2007/07/25(Wed) 12:28)
>違うと思います,温度が同じなら,不純物半導体でも,真性半導体でも,価電子帯から伝導帯へ励起される電子の数は同じだと思います.
不純物半導体の価電子帯から伝導帯に励起され,また, 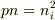 に従うために再結合される電子を考慮した電子は,真性半導体の価電子帯から伝導帯に励起される電子と比べると,小さいことがわかります.
に従うために再結合される電子を考慮した電子は,真性半導体の価電子帯から伝導帯に励起される電子と比べると,小さいことがわかります.
と書いてもやっぱり違いますか?
また,不純物半導体でも真性半導体でも,価電子帯から伝導帯へ励起される電子の数が等しいというのは式で表すと,
真性半導体のときに,価電子帯から伝導帯へ励起される電子の数をnとすると
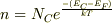 で,不純物半導体のときに,価電子帯から伝導帯へ励起される電子の数をn’とすると,
で,不純物半導体のときに,価電子帯から伝導帯へ励起される電子の数をn’とすると,
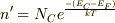 となり,
となり, 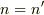 になるということですか?
になるということですか?
一方,言葉で表すと,真性半導体でも,不純物半導体でも,エネルギーギャップは等しいので,価電子帯から伝導帯に励起される電子の数が等しい.
これであっているでしょうか?