threeaster さんの書込 (2007/07/03(Tue) 11:17)

はじめまして，threeasterです． 大学一年(教養・理系)です．

先日，"大きい風船と小さい風船を管で連結すると，(授業中の実験 で見たとおり，)大きい風船はさらに大きくなり，小さい風船はさ らに小さくなる．このことを力学的，熱力学的などのモデルを作り ，考察しなさい．"というレポートの課題が出ました．

大きいほうの風船の方が内圧が低いのだろうという予想はついたも のの，それ以上の考察ができなかったので，調べてみると，シャボ ン玉でも同じような現象が起こるとわかり，次のサイトに行き着き ました．

(大小のシャボン玉のゆくえ)

• http://www8.plala.or.jp/grasia/daisho.htm

風船を球体と近似して，このサイトの"2)球面の場合"をベースに考 えようと思っているのですが，なぜ表面張力が一定になるのかわか りません．なぜ表面張力が一定になるのかを説明していただけない でしょうか．(とくにゴムの場合でお願いします．)

お願いします．

zoro さんのレス (2007/07/03(Tue) 11:42)

threeasterさん，初めまして．

表面張力というのを良く知りませんが，ご紹介のサイトの「球面」の場合の最後に；

＞文献注）1によるとセッケン膜の場合は表裏二つの膜があるという考えで次式を提示している．

という記述があります．此れから逆に考えると，「表面張力は，考察する塊の裏表の表面に発生するが，その塊の内部では圧縮応力はできても，引き離されるのに対抗する引力型の応力は無い」と思われます．少なくとも，液体やゴムでは，このような可能性が高いのではないでしょうか．

恐らく，表面張力の解説を探して，考察すると良いように思います．

toorisugari no Hiro さんのレス (2007/07/03(Tue) 13:56)

解説ではないですが．

> なぜ表面張力が一定になるのかわかりません．なぜ表面張力が一定になるのかを説明していただけないでしょうか．

逆に質問ですが，高校でバネについて 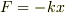と習ったと思いますが，何故，バネにおいてバネ定数は一定と考えられるのでしょうか?

そこら辺から考えてはどうですか?

トンガリ さんのレス (2007/07/03(Tue) 20:22)

「なぜシャボン玉の表面張力が一定でしょうか」の質問に苦慮する． セッケン液の表面張力はシャボン玉の大きさに関係なく一定を保つ． 半球Ｒの表面積および受圧面積はＲの２乗に比例する． 二つの半球の合わせ面の円周長はＲの１乗に比例する． を考慮すれば，シャボン玉に関しては何の疑問もない．

風船のゴムの弾性の仮定は下記でよい． 【比例】：ゴムの張力は風船が小さく伸びの小さい間は伸びに比例し， 【一定】：風船が大きく，伸びが大きくなると，以後の張力は一定．

風船大小共に【一定】の場合は，シャボン玉と同じで，大きな側が膨らむ． 風船大が【比例】で風船小が【一定】の場合・・・・・ 風船大小共に【比例】の場合・・・・・・・・・・・・・・・・・・・

threeaster さんのレス (2007/07/04(Wed) 01:27)

レスありがとうございます．

>逆に質問ですが，高校でバネについて 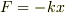と習ったと思いますが，何故，バネにおいてバネ定数は一定と考えられるのでしょうか?

ええと，私の理解している範囲では，統計力学的にはもっと複雑な式になる(手元の資料(先生自作の教科書)によると 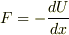( :力， :ばねの持つポテンシャル， :変位))けれども，それをテイラー展開して一次近似した結果で，この近似は が十分小さいときだけ成り立ち， が大きくなると二次以上の項の影響が大きくなって，近似が成り立たなくなると理解しています(弾性限界)．

さて，ここまで考えて，

>風船のゴムの弾性の仮定は下記でよい． >【比例】：ゴムの張力は風船が小さく伸びの小さい間は伸びに比例し， >【一定】：風船が大きく，伸びが大きくなると，以後の張力は一定．

についてなんですが，これは，風船が余り膨らんでいないときはフックの法則が成り立ち(力が変位の一次近似で表され)，風船の膨らみが大きくなると，弾性限界をむかえ，一定とみなしていいということですよね．

とすると，多分私が何か混乱していたのは，風船がある程度大きいときも，フックの法則が成り立っていたと考えてモデルを立てていて，さらにそれが表面張力の場合とごっちゃになっていたからだと思います．

>風船大小共に【一定】の場合は，シャボン玉と同じで，大きな側が膨らむ． >風船大が【比例】で風船小が【一定】の場合・・・・・ >風船大小共に【比例】の場合・・・・・・・・・・・・・・・・・・・

について考えてみたんですが，風船が小さいときに弾性が比例になるのだから，二行目のようにはならないのではないかと感じました． 考えるべきは [1]大:一定小:一定 [2]大:一定小:比例 [3]大:比例小:比例 だと思うのですが……． もしこうだとすると，[1]はシャボン玉と同じ，[2]は 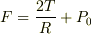(単位はリンク元と同じ)より小では圧力が半径と無関係になるので，結局大が膨らんで系全体の圧力を小さくしようとする．[3]では，大も小も圧力と半径が無関係になるので安定，動かない と考えたのですがこれでよいでしょうか．

>「なぜシャボン玉の表面張力が一定でしょうか」の質問に苦慮する．

についてなんですが，表面張力に関して調べてみると，

"液体内の分子は周りから引力で引かれているのに対して，表面上にある分子は液体に触れていない部分だけ，液体分子の引力の影響を受けていない．その分だけ，表面上にある分子は余ったエネルギーを持つことになり，これが表面張力の強さとなる．"(ウィキペディア)

とありました．こう考えてみると，確かに表面張力が一定なのは当たり前ですね．分子ひとつの立場に立ってみれば，周りにいる分子の数は同じようなものですから，表面張力は一定になりますね．

多分，ゴムの張力をフックの法則で考え，それの延長で表面張力を考えていたので，混乱していたのだと思います．

表裏二つの膜などのことも考慮しつつ考えれば多分うまくいくと思います．ありがとうございました．

トンガリ さんのレス (2007/07/04(Wed) 09:21)

二行目を誤記訂正 ＜誤＞風船大が【比例】で風船小が【一定】の場合・・・・・ ＜正＞風船大が【一定】で風船小が【比例】の場合・・・・・

従って，threeasterさんの組み合わせの分類 [2]大:一定小:比例 が正しい．

トンガリ さんのレス (2007/07/04(Wed) 13:25)

シャボン玉に関しては 半球Ｒの表面積および受圧面積はＲの２乗に比例する． 二つの半球の合わせ面の円周長はＲの１乗に比例する． 内圧は表裏で2倍ｘ表面張力ｘ円周長／受圧面積すなわち1/Ｒに比例する． ただし，内圧は外圧Ｐoを基準に増加分で表した．

ゴム風船に関して弾性限界内においては [Ｌ]ゴム紐では張力／長さの伸びにフックの法則が成り立つ． [Ｐ]ゴム膜では張力／面積の伸びにフックの法則が成り立つ． 半球ＲoがＲに膨らんだ場合，ゴム膜張力は（Ｒ／Ｒo)^2 に比例する． 内圧はゴム膜張力ｘ円周長／受圧面積（Ｒ／Ｒo)^2／ＲすなわちＲの１乗に比例する．

threeasterさんの?内圧が半径と無関係になる?との主張は[Ｌ]に基づくかのもので， 賛同できない，私は[Ｐ]に基づき?内圧はＲの１乗に比例する?と主張する．

?ゴムのポアッソン比は特殊で，0.5に近く，引っ張られて変形しても体積変化が無い?と聞きます．

ヒース さんのレス (2007/07/05(Thu) 06:33)

トンガリさんへ

もし内圧はＲの１乗に比例すると考えると，実験の結果と矛盾してしまうのではないでしょうか？

−１乗の間違いでは？？

トンガリ さんのレス (2007/07/05(Thu) 12:31)

ヒースさんへ 単なる間違いではありません．実験条件が異なり，紐と膜の対立があるからです．

二つの風船がある程度大きく膨らんでいてゴムの弾性限界を越えて，張力が一定とみなしていい場合は， ?内圧は半径の−１乗に比例する?と，threeasterさんと私の見解は一致している． ?大きな風船の側がより大きく膨らむ?とのthreeasterさん実験結果に矛盾しない． 以上に関しては争点がない．

風船が余り膨らんでいないときでフックの法則が成り立つ場合は，threeasterさんと私の主張が分れる． (threeasterさん）ゴム紐では張力／長さの伸びにフックの法則が成り立ち，?内圧が半径と無関係になる? (私トンガリ） ゴム膜では張力／面積の伸びにフックの法則が成り立ち，?内圧は半径の１乗に比例する? この条件を満たすのは，新品の風船をチョットだけ膨らませる実験で，未だ行われていないと理解する．

既に行なわれた実験結果に歩み寄るべく思考するなら， ゴム膜の張力が半径の１乗未満(例えば0.5乗)に比例するならば，?大きな風船の側がより大きく膨らむ?

実際のゴム膜の張力は始めは比例し弾性限界を越えたら一定と仮定する様な単純なものではありません． これまでの論拠とした，紐での，Ｘ軸が伸び・Ｙ軸が張力のグラフで比例から一定に変わる折線の仮定よりも， ＹがＸの例えば0.5乗に比例するグラフの仮定の方が，ゴム膜の性質をより現実的に表現している． だから，アタリキ大概の風船の実験では?大きな風船の側がより大きく膨らむ?のです．

zoro さんのレス (2007/07/05(Thu) 17:54)

素人目でも，

＞二つの風船がある程度大きく膨らんでいてゴムの弾性限界を越えて，張力が一定とみなしていい場合は，

というのは，状況が目の前に浮かぶ様です．

＞この条件を満たすのは，新品の風船をチョットだけ膨らませる実験で，未だ行われていないと理解する．

是非とも，2つの風船と3方向バルブとで実験出来そうですが，やっていただいて実験レポートを載せていただけたらうれしいですが...．