基礎かも

home > 掲示板 >

このページのPDF版

サイトマップ

基礎かも

パン子さんの書込 (2007/07/01(Sun) 21:23)

はじめまして

あのぉ，基礎中の基礎で，聞くのが変かもしれませんが，力学の mv=一定と言うのは本当なのでしょうか？質量と速度が同じ重みなんですか？

Re: 基礎かも

クロメルさんのレス (2007/07/02(Mon) 01:49)

はじめまして，パン子さん．質量と速度の積がいつも同じ大きさということですか？それなら本当です．ｍｖ＝一定だけでは，一粒子になってしまうので全粒子に書き直すと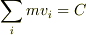， $\sum_i mv_i=C$ Cはある定数で，Σとiは全粒子の運動量の和を表します．

運動量は，速度をやりとりするときの，基本単位ということになるのかな．ある粒子が運動量Pを失ったとすると，ほかの粒子がPを受け取るみたいな感じです．ただし，これは外から加える力がないときです．

例えば，電子１が運動していて，電場によって力をうけとったとすると，その電場を作っている荷電粒子２の受ける反作用を考えずに，電子１だけの運動量をみると，もちろん一定ではありません．でも，電子１と荷電粒子２の運動量との和は一定です．

Re: 基礎かも

パン子さんのレス (2007/07/02(Mon) 14:56)

回答ありがとうございます．

例えば１kgと1m/sは同じレベルの扱いとしていいのでしょうか？ホコリが1m/sで動いてるのと，1kgの鉄アレイが超微妙に動いてるのが同じ運動量？って思いました．実際に目で見れればいいのですが，そんな実験道具が手元にないもので．

ここからは勝手な考えですが，全く同等に扱えるならこの世の中からどちらかの変数を消去できるんじゃないかなぁとか思ったりしました．

Re: 基礎かも

zoro さんのレス (2007/07/02(Mon) 18:16)

パン子さん，初めまして．面白い考え方ですね．

いま二つの物体，a,b が在るとします．そしてそれらを正面衝突させて，止まる為の条件を求めようとします．

さて，それらの質量と速度，そして運動量は，

物体質量速度運動量 aMaVaPa = Ma*Va bMbVbPb = Mb*Vb

ですから，同じ運動量の物体を逆向きにぶつければ，運動量が相殺されて(Pa - Pb = 0)，両物体は静止しますね．

ですから，次のように一見すると，とても違う運動をしている場合でも，

(Ma = 2mg, Va = 3km/s) (Mb = 6Mg, Vb = 1μm/s)

運動量を求めてみれば；

Pa = 2mg * 3km/s = 2x10^(-3)g * 3x10^(+3)m/s = 6g・m/s) Pb = 6Mg * 1μm/s = 6x10^(+6)g * 1x10^(-6)m/s = 6g・m/s)

と同じ運動量ですから，物体が破壊されない限り衝突後に静止する訳です．

このような結論を得るのには，質量と速度は別々の物理量としておくのが良いのだとおもいます．

上の例は，時間を逆に辿れば，静止した物体があって，その質量,Mc が

Mc = Ma + Mb

に分裂するするとした時の速度の比を求める事ができるとも考えられます．

〜〜〜

それにしても，

＞全く同等に扱えるならこの世の中からどちらかの変数を消去できるんじゃないかなぁ

と思ったのは凄い感性だと思います．どんどん，不思議だとおもった事を書き込んでください．

Re: 基礎かも

クロメルさんのレス (2007/07/03(Tue) 01:08)

うーん，そういうことですか．残念ながら，そういうことはできませんね．

運動量が決定したら，質量か速度のいづれかが出てくるのではないです．

運動量は，速度と質量を両方決定して，初めて定義できる量です．たとえば，1[m/s]のホコリといった時でも，どんなに小さくても質量はありますから，いいかげんな値かもしれませんが，10^(-9)[g]とか質量があって，そこで，10^(-9)[gm/s]と運動量が決定するんですよ．

おおざっぱにいえば，運動量はある物体にぶつかったときに，その物体をどれくらいの勢いを与えるか（はじきとばすか）の目安になります．

逆に，運動量を一定にしたときには，比較的軽い物体だが速度が速いとか，重い物質だが速度がおそいということになりますが，気を付けてほしいのは，速度も質量も別の概念で，それぞれ（運動量一定というときには，積が一定という関係をもって）別々に決定します．単位の境界があいまいになるということはないです．

Re: 基礎かも

zoro さんのレス (2007/07/03(Tue) 01:57)

クロメルさん，横から失礼ですが．

最近のスレッドでSI単位系での物理量の表現を調べました．その結果；物理量 =(ある単位による数値部）x（ある単位) の様です．

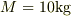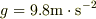例えば，質量， $M=10\mbox{kg}$ の物体が，地表で地球に引っ張られる力は，重力加速度， $g = 9.8\mbox{m}\cdot \mbox{s}^{-2}$ とすれば，

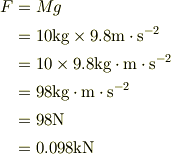
$F &= Mg\\&= 10\mbox{kg} \times 9.8\mbox{m}\cdot \mbox{s}^{-2} \\&= 10\times 9.8 \mbox{kg} \cdot \mbox{m}\cdot \mbox{s}^{-2}\\&= 98 \mbox{kg} \cdot \mbox{m}\cdot \mbox{s}^{-2}\\&= 98 \mbox{N}\\&= 0.098 \mbox{kN}$

＃SI単位系では単位と単位の間には，区切り記号として，「・」か「空白」を入れるようになっていると思います．＃Wikipediaでは，「・」を入れる事が多いようです．＃個人的には，「・」の方が見間違いが少ないと思うので好きです．＃でも「・」，バレット，の前後の空白が少し詰めた方が良いとおもいます．

また，2007年度版の高校の物理の教科書を数冊購入した結果，単位をわざわざ「[」と「]」とで括らない場合も散見されています．要は，混在です．

私見としては，括弧で括るのは；

物理量に対するイメージを低下させる
次元との混同をし易い

ので，中止するべきだと思います．その代わり，

指数部を表す「接頭辞」と 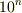$10^{n}$ の代表例は，練習すること

例えば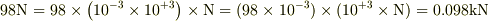， $98 \mbox{N} = 98 \times \left( 10^{-3}\times 10^{+3} \right) \times \mbox{N} = (98 \times 10^{-3}) \times (10^{+3} \times \mbox{N}) = 0.098\mbox{kN}$

が大切だと思います．

ちょっと脱線しましたが，「単位」関連で，お許しください．

Re: 基礎かも

Joh さんのレス (2007/07/03(Tue) 02:15)

速度と質量を掛けた量を運動量と呼んでいるのであって，速度と質量が等価な概念だという結論はおかしいと思います．

例えば，乱暴に言えば国の税収は『働いている人の人口』×『平均所得』にだいたい比例すると思いますが，『労働人口が多い』×『賃金が安い』という国と，『労働人口が少ない』×『賃金が高い』という国では，総税収はだいたい同じかも知れません．だからと言って，『人口』と『収入』という概念を等しく見るという議論は間違いでしょう．変数を消去するという言い方は，おかしいのです．

単に運動量が大きいと言ったとき，それは質量が大きいのか，速度が大きいのかは明示的にわかりません．運動量だけを考えるとき，それはどちらでもいいわけで，運動量という概念には，この『どちらでもいい』という部分が既に内包されています．また，それが，新たに運動量という概念を考え出した便利性なのです．パン子の言う『質量が大きいのか，速度が大きいのか区別できない』という点こそが，まさに運動量を定義した旨味の一つとも言えます．

Re: 基礎かも

パン子さんのレス (2007/07/03(Tue) 18:14)

ごめんなさい…消せたら楽かなぁって思っただけです．

みなさんありがとうございました．また一つ勉強になりました．

[home] [掲示板] [ページの先頭]