平行板コンデンサー
平行板コンデンサー
M さんの書込 (2007/07/01(Sun) 20:18)
これは,大学の宿題として出された問題です.
問:平行版コンデンサーでの極版間に電場Eをかけ,この電場に垂直に磁場Bをかけた.電荷-eの電子が−極版から初速度0で飛び出したとき,電子の運動はどうなるのか調べたい. (1)電子の質量をm,速度をvとして,運動方程式を経立てよ.また,適当な座標軸を決めて,各成分に分けて表せ. (2)初期条件(t=0でv=0)の元に運動方程式を解いて,時刻tでの電子の速度を求めよ.
私はこの問題で,
+−−−−−−−−−−−−−−−−−−
|E |↑ |○→ ↓↓
-−−−−−−−−−−−−−−−−−−
このような図を考えました.また座標軸を,この図の下から上方向をy軸,左から右方向をx軸として定めました. ○で表したのは電子であり,その周りにある矢印は電子に働く力のことです.磁場はこの平面を表から裏に突き抜ける向きに働いてるとします.
そして運動方程式は ・y軸方向
m*d^2y/dt^2=qe-mg
・x軸方向
m*d^2x/dt^2=qvB
と立てました.
運動方程式の立て方はこれで合っているのでしょうか?? また,ここから初期条件を使って電子の速度を求めるにはどのようにすればいいのでしょうか?
Re: 平行板コンデンサー
yama さんのレス (2007/07/01(Sun) 21:18)
ちょっと違うようです・ 磁場からはたらく力 qv×B をx成分とy成分に分けて運動方程式に取り入れる必要があります.
Re: 平行板コンデンサー
M さんのレス (2007/07/01(Sun) 21:21)
qvBってどのような方向に働くのですか??
Re: 平行板コンデンサー
yama さんのレス (2007/07/01(Sun) 22:09)
ベクトルの外積なので,速度にも磁場にも垂直な方向になりますが,運動方程式にあてはめるには外積を成分で表せばいいでしょう.
Re: 平行板コンデンサー
tip★ さんのレス (2007/07/01(Sun) 23:59)
磁場の向きが紙面の表から裏なのか,裏から表なのかで働く力の向きも変わってくると思います.
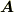 ×
× 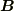 の向きは,
の向きは, 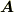 から
から 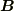 へ右ねじが進む方向(表現がおかしいかな・・・(汗))です.
へ右ねじが進む方向(表現がおかしいかな・・・(汗))です.
したがって 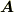 ×
× 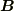 と
と 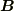 ×
× 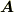 は大きさは同じだけど向きが逆ということになると思います.
は大きさは同じだけど向きが逆ということになると思います.
Re: 平行板コンデンサー
yama さんのレス (2007/07/02(Mon) 00:00)
速度の方向は磁場の影響で変化します.
磁場からはたらく力は 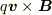 なので,これを成分に分けてみてください.
x成分が
なので,これを成分に分けてみてください.
x成分が 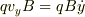 ,y成分が
,y成分が 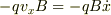 になることが分かると思います.
になることが分かると思います.
Re: 平行板コンデンサー
M さんのレス (2007/07/02(Mon) 00:49)
今回の場合,磁場から働く力はx軸方向だけではないのでしょうか? もしかしてこれは私の勘違いでしょうか?
Re: 平行板コンデンサー
tip★ さんのレス (2007/07/02(Mon) 01:26)
磁場の向きが紙面の裏から表だったら,ローレンツ力の働く方向は+x軸方向だと思います.
↑速度が右斜めになるのでローレンツ力が働く方向は変化しますね・・・すいません.
Re: 平行板コンデンサー
yama さんのレス (2007/07/02(Mon) 07:17)
最初はx軸方向だけにはたらきますが,それによってx軸方向の速度成分が生じます.その結果y軸方向にも力がはたらくことになります.
なお,No.16676で書いた式は,磁場が+zの向きの場合です.また当然 q=-e です.
Mさんの式では電場からはたらく力も間違っているように思われます. 電場からはたらくy方向の力は -qE=eE になります.
さらに,問題文には極板が置かれている方向については何も書かれていないので,重力の方向が分かりません.おそらく重力は無視して考えるのでしょう.
Re: 平行板コンデンサー
M さんのレス (2007/07/02(Mon) 12:45)
重力を無視していいということは,働く力は「電場からはたらく力」と「磁場からはたらく力」の2種類ということですよね?
そして,磁場から働く力はt=0の時ではx軸方向だけですが,t>0の時では,x軸y軸両方にはたらくということですよね?
このような時は例えば,働く力とx軸とのなす角度をθなどとおいて,x軸成分y軸成分に分ければいいのでしょうか??
Re: 平行板コンデンサー
yama さんのレス (2007/07/02(Mon) 13:43)
>重力を無視していいということは,働く力は「電場からはたらく力」と「磁場からはたらく力」の2種類ということですよね?
そうです.
>そして,磁場から働く力はt=0の時ではx軸方向だけですが,t>0の時では,x軸y軸両方にはたらくということですよね?
厳密にいえば初速度が0なので,t=0 のときは磁場からの力は0です.微小時間後には磁場からx軸方向の力がはたらき,さらにしばらくするとy軸方向の力もはたらくようになります.
>このような時は例えば,働く力とx軸とのなす角度をθなどとおいて,x軸成分y軸成分に分ければいいのでしょうか??
θを用いて表すこともできますが,運動方程式をつくる場合は速度の成分を用いたほうがいいでしょう.そうするとNo.16676のようになるわけです.
Re: 平行板コンデンサー
M さんのレス (2007/07/02(Mon) 20:40)
では,今回の場合少しでも時間がたつとx軸方向にも速度が生まれてくるので,x軸方向とy軸方向に速度を持っていることになります. そこで x軸方向の速度をVx y軸方向の速度をVyとします.
すると運動方程式は x軸方向:m*d^2x/dt^2=eVyB y軸方向:m*d^2y/dt^2=eE-eVxB となります.
これで合っているでしょうか?
Re: 平行板コンデンサー
yama さんのレス (2007/07/02(Mon) 22:24)
q=-e なので一部の符号が違うようです.
x軸方向:m*d^2x/dt^2=-eVyB y軸方向:m*d^2y/dt^2=eE+eVxB
となりますが,VxやVyを座標の時間微分で表すと,運動方程式は結局次のようになります.
x軸方向: 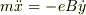 y軸方向:
y軸方向: 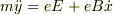
Re: 平行板コンデンサー
M さんのレス (2007/07/02(Mon) 22:32)
yamaさん,親切にありがとうございます. でも思ったのですが,この場合は磁場を紙面の表から裏に突き抜ける向きとしているので,やはりx軸方向に働く力はx軸方向正の向きではないのでしょうか?
あと,これで運動方程式が立てられたとしても,初期条件を用いた運動方程式の解き方がわかりません. 先生が海外出張にいってしまったので質問することもできません. 基本的なことだと思いますが,もしよろしければ教えていただけますか?
Re: 平行板コンデンサー
zoro さんのレス (2007/07/02(Mon) 22:33)
Mさん,横から失礼します.
座標系の取り方が良くわかりませんが,例えば,下図のような右手座標系を採用します;
<pre>
+y軸
↑
|
|
|
・y=+d/2の無限面に,電荷面密度, 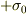 |
|
|
|
|
|
|
・ーーーーーーーーーーーーー→+x軸
/|
/|
/|
+z軸|
|
|
|
・y=-d/2の無限面に,電荷面密度,
|
|
|
|
|
|
|
・ーーーーーーーーーーーーー→+x軸
/|
/|
/|
+z軸|
|
|
|
・y=-d/2の無限面に,電荷面密度, 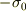 |
|
</pre>
電場は(-d/2 < y < d/2)の領域では;

磁束密度は,「表から裏に突き抜ける向き」となっているので

運動方程式は;
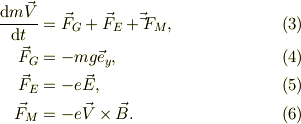
なおベクトルの外積は,任意の2つのベクトルに対して;
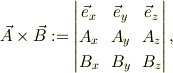
を用いて,計算する事をお勧めします.
Re: 平行板コンデンサー
M さんのレス (2007/07/02(Mon) 22:56)
zoroさん,丁寧に図までありがとうございました.本当にありがたいです. しかし恥ずかしいことながら,頭の中が混乱してきました. zoroさんのやり方でFmを求めると,x軸正の方向にFm=eVBとなってしまうのですが..... どこか間違えましたかね....?^^;
Re: 平行板コンデンサー
zoro さんのレス (2007/07/02(Mon) 23:06)
>x軸正の方向にFm=eVB
と書かれていますが,この「V」とか「B」とは何ですか?
問題を解くには,数式の定義が明確になされていないと意思疎通は計れません.
特に,ベクトルの外積は,間違え易いので,丁寧に考えて下さい.ヒントは,
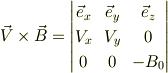
Re: 平行板コンデンサー
yama さんのレス (2007/07/02(Mon) 23:17)
>でも思ったのですが,この場合は磁場を紙面の表から裏に突き抜ける向きとしているので,やはりx軸方向に働く力はx軸方向正の向きではないのでしょうか?
なるほどそのとおりですね.私は磁場はz軸の正の向きとしていたのですが,裏向きならば Bz=-B になるので,運動方程式は次のようになりますね.
x軸方向: 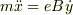 y軸方向:
y軸方向: 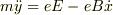
Re: 平行板コンデンサー
M さんのレス (2007/07/02(Mon) 23:18)
zoroさん,ありがとうございます!!! 解いた結果 Fm=VyBoEx-VxBoEy となりました.ここでExとEyはそれぞれx軸y軸の方向ベクトルです. TeXが使えないもので↓↓わかりにくくて申し訳ないです.
とするとやはり,No.16700で私が立てた運動方程式でいいということでしょうか? もしかして,これも間違ってますか..........?^^;
Re: 平行板コンデンサー
M さんのレス (2007/07/02(Mon) 23:21)
yamaさん,ちょっと私たちの会話噛みあってなかったですね.... 私が分かりにくい説明したのが悪いです.申し訳ありませんでした. でもおかげさまで運動方程式は立てることができました.感謝します.
でもこれを解くにはどうすればいいことやら........↓↓
Re: 平行板コンデンサー
yama さんのレス (2007/07/03(Tue) 00:14)
運動方程式は次のようにして解くことができます. y方向の式に i を掛けてx方向の式に加え,x+iy=u と置くと,運動方程式は次のようになります.
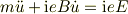
これは非斉次形の線形微分方程式なので簡単に解けます.
まず 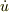 について解き,複素数の積分定数Cを,実数の定数a,αを用いて
について解き,複素数の積分定数Cを,実数の定数a,αを用いて 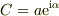 と置き換えます.
そして
と置き換えます.
そして 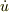 を実部と虚部に分ければ
を実部と虚部に分ければ 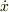 と
と 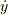 が求まります.定数の値は初期条件によって決まります.
が求まります.定数の値は初期条件によって決まります.
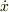 と
と 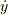 をさらに積分するとxとyが求められます.
をさらに積分するとxとyが求められます.
Re: 平行板コンデンサー
zoro さんのレス (2007/07/03(Tue) 00:52)
y amaさんへの補足です.
運動方程式には,速度としては,Vx,Vyしか出てきません.そこで,2次元ベクトル空間の表式は,2次元空間としての複素平面に1対1で対応するので,式が見通し良く,計算も楽になります.近くのスレッドで書いた図を,自己引用します;
<pre> +y軸
↑
- |

- Y・ーーーーーー・P
|/|
|/| 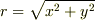 |r /|
|r /| 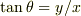 |/|
|/|
|/
|/|
|/|
|/  |
+ーーーーーー・ーーー→ +x軸
|
+ーーーーーー・ーーー→ +x軸
O X
</pre>
そこで,
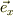 → 「1」
→ 「1」
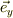 → 「i」
と読み替えます.
→ 「i」
と読み替えます.
例えば,
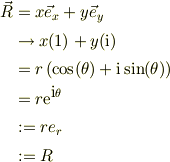
当たり前の事ですが,
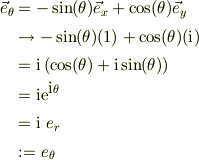
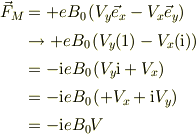
とかに書き換えられますね.
このように,2次元ベクトル空間の表式は,2次元空間としての複素平面に1対1で対応するので,計算がとても楽になります.
速度ベクトル;
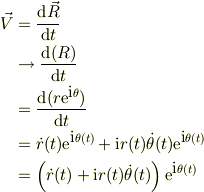
から求められると簡単だと思います.同様に加速度ベクトルも算出出来ますね.
なお,単位複素ベクトルで書き直すと,
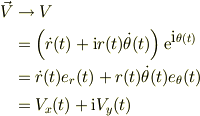
と,極座標表示の速度ベクトルを複素数表示で得る事ができます.
逆に言えば,極座標表示の2次元ベクトル表現と複素数表現では
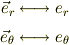
の対応関係を用いて,自由に行き来出来る訳です.世の中の問題の95%ほどは,2次元平面で記述できるので,この関係に慣れていると,とても計算が,解り易く,間違いにくいものになりますよ.
なお,オイラーの公式を利用した変形以後は,y amaさんの解説の範囲外ですので,ご留意ください.
Re: 平行板コンデンサー
zoro さんのレス (2007/07/03(Tue) 18:43)
複素数による計算法の説明がゴチャゴチャになったので, ・2007/07/02(Mon) 22:33 No.16703 での運動方程式をどう表現するかにもどります.見やすさの為に,再引用します;
〜〜〜引用初め 電場は(-d/2 < y < d/2)の領域では;

磁束密度は,「表から裏に突き抜ける向き」となっているので

運動方程式は;
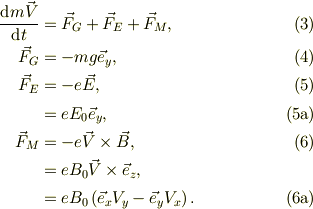
〜〜〜引用終り
外力には速度の成分しか無いので,上の運動方程式で, 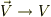 とするように,デカルト座標系で変換します.
とするように,デカルト座標系で変換します.

その結果
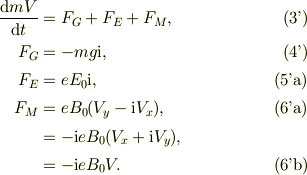
一本の式に纏めると,
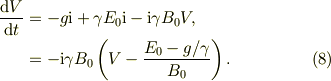
ここで,電子の電荷質量比;

式(8)は,一見すると面倒な式ですが,よく見ると変数分離型ですので,慌てずに積分してみて下さい.
速度が判れば,さらに積分して位置が求められますね.
なお,式(8)は,まだ操作しにくいと思いますので,パラメータを次に定義します;
磁場による回転の(サイロトロン)角振動数
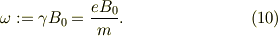
速度成分の常数;

すると,式(8)は;
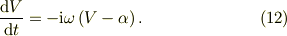
となります.
残念な事に,ケアレスミスのチェックは未完ですので,参考程度にして下さい.流れはあっている思います.
Re: 平行板コンデンサー
M さんのレス (2007/07/04(Wed) 11:10)
返事が遅くなって申し訳ありません. とてもわかりやすい説明ありがとうございました. たったいま解いてみたのですが V=Ce^(-iωt)+α オイラーの公式より V=C{cos(ωt)-isin(ωt)}+α 初期条件(t=0 -> v=0)より 0=C{cos(0)-isin(0)}+α よってC=−α これらより V=-α{cos(ωt)-isin(ωt)}+α//
これであっているでしょうか?
Re: 平行板コンデンサー
zoro さんのレス (2007/07/04(Wed) 12:15)
>V=-α{cos(ωt)-isin(ωt)}+α//
これで合っていると思われます.この式を実部,虚部に分けて,通常のベクトルに戻せば;
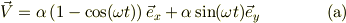
ですね.私の予測では「常数項が出てくるのは,y方向と思っていた」ので混乱しています.というのも加速する源である「重力と電場」は共に,y方向しか持たないからです.
実際に,V=α[1-exp(-iωt)]について積分すると判るように,時間に比例する部分は,実部に入っているので....
あ,でも式(a)をこうして見ていると,一種の周期的回転ですから,「x方向のドリフト+回転」と考える事が出来るのかも知れません.
![\vec V = [ \alpha \vec e_x ] -\alpha [ \cos(\omega t)\vec e_x -\sin(\omega t) \vec e_y ] \tag{b}](http://hooktail.maxwell.jp/bbslog/92b2ec0a9ca3518d9c22cbcc2967aafb.png)
そういえば,ホール素子の起電力と似た感じですね.あと一押しかも.
Re: 平行板コンデンサー
zoro さんのレス (2007/07/04(Wed) 19:25)
【解いてみたものの】
今回の問題は,簡単に書いてみると,(x,y)平面での微分方程式;
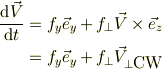
ここで, 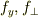 は適当な定数とする.
また,
は適当な定数とする.
また, 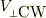 は
は  を時計方向に π/2回転したもの.
を時計方向に π/2回転したもの.
となります.そして,その解は,スレッドを開かれた Mさんが既に解かれた通りだと思います.
しかし,私には,気になる点が,2つ残っています.
●質問1
もし, 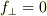 とすると,
とすると, 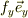 の単純加速で,y軸に沿って速度が時間ともに変化するだけである.しかし,
の単純加速で,y軸に沿って速度が時間ともに変化するだけである.しかし, 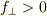 となった瞬間から,y軸への単純加速は消えて,むしろ x軸への定速度成分が現れて来る.
となった瞬間から,y軸への単純加速は消えて,むしろ x軸への定速度成分が現れて来る.
これをどのように考えれば宜しいのでしょうか?
●質問2
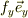 には,普通,電場だけを考えて,電場と磁場との印可により,両者に垂直な方向にドリフト成分がでるといった解釈を見た様な気がしていました.
には,普通,電場だけを考えて,電場と磁場との印可により,両者に垂直な方向にドリフト成分がでるといった解釈を見た様な気がしていました.
今回の計算で偶然重力の影響を取り入れた訳ですが,そういう意味では,y方向にある種の加速度が発生するだけで,ドリフトが発生する訳です.
となれば,極端に大きい加速センサとなる可能性があるとも考えられますが,どうなんでしょうか?
Re: 平行板コンデンサー
yama さんのレス (2007/07/04(Wed) 22:53)
質問1については,次のように考えることができると思います.
運動方程式の初期条件の違いによって,いろいろな特殊解が可能なわけですが,その特殊解の1つとしてx軸方向の等速直線運動が可能であり,その場合は電場からの力と磁場からの力がつりあっています. 非斉次方程式の一般解は,この特殊解(等速直線運動)と斉次方程式の一般解(円運動)との重ね合わせになるので,この等速直線運動がx軸方向の定速度成分になると考えることができるでしょう.
なお,等速直線運動と円運動の重ね合わせは,一般にトロコイドを描くことになりますが,特別な場合として今回の問題のように初速度が0であればサイクロイドを描くことになるでしょうね.
また,磁場が弱いほど,x軸方向の定速度成分が大きくなりますが,これは磁場が弱いほど運動方向が変わりにくいため,運動方向がx軸方向に変わったときに大きい速度に達しているためでしょう.
Re: 平行板コンデンサー
zoro さんのレス (2007/07/04(Wed) 23:52)
>質問1については,次のように考えることができると思います.
あ,そうですね.幾つかの勘違いが積み重なって,可笑しくなっていたようです.
恐らく, ・直接積分しているから,完全解の筈.と思いながら,初期条件をV(t=0)=0としていた. ・斉次方程式の一般解(円運動)を出しはしたのですが,これも初期条件をV(t=0)=0としたので,ゼロ解となって,トリビアル! ・ただ,今でもy軸の力が,直接的に y軸への速度成分に寄与しないのは「不思議」ですね.
お恥ずかしい事に,トロコイドは始めて知りました.御蔭で,何となく判りました(汗,笑).
>磁場が弱いほど,x軸方向の定速度成分が大きくなりますが,...
このご指摘は重要ですね.有り難うございました.自分なりにもう少し検討してみます.
〜〜〜 最近は,紙細工の落下回転でも,落下に垂直な方向に運動が生じる事が観察されて驚きましたが,「磁場よ,お前もか!」の心境です.天国で,ホールさんが,「それはコチラの台詞だ!」と言われているかも.
Re: 平行板コンデンサー
zoro さんのレス (2007/07/19(Thu) 21:37)
以前書いた複素数による速度の微分方程式;
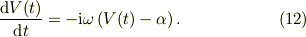
で,なせ純粋にy方向( 純虚数)の定数項が出ないで,x方向に定数項が出てくるのかを差分計算で求めたものの,そのままで忘れていました.ノートが出て来たので,簡単にメモにします.
〜〜〜 問題は,時刻0からゼロ・スピードで始まった速度V(t)がどのような時間の関数になるかです.変数分離ですぐに計算ができるものの,どうしてy方向の定数項が無いのが不思議でした.今となっては,磁場の存在により,「直線運動はないのさ」という事なのかも知れませんが.
〜〜〜 時刻,0 〜 tまでをN等分にします.

任意の時間軸は離散的になります;
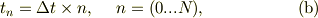
そこで,式(12)を変形して;
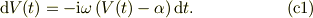
また,関数の展開から
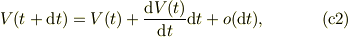
これらに対して,その時間点を離散化して,次のように書きます;
![\Delta V[n] &\sim -\mbox{i}\omega \left( V[n] -\alpha \right)\Delta t,\\V[n+1] &= V[n] +\Delta V[n], \tag{d1}\\&\sim V[n] -\mbox{i}\omega \left( V[n] -\alpha \right)\Delta t, \\&= \mbox{i}\alpha\omega\Delta t +V[n](1 -\mbox{i}\omega\Delta t),\tag{d2}](http://hooktail.maxwell.jp/bbslog/5fa38500b1cf804cd7bdbec402aa1c78.png)
式(d2)が離散化した速度配列の漸化式と考えられます.具体的に,幾つかを羅列すると;
![V[0] &= 0,\\V[1] &= \mbox{i}\alpha\omega\Delta t +V[0](1 -\mbox{i}\omega\Delta t) ,\\&= \mbox{i}\alpha\omega\Delta t,\\V[2] &= \mbox{i}\alpha\omega\Delta t +V[1](1 -\mbox{i}\omega\Delta t) ,\\&= \mbox{i}\alpha\omega\Delta t +\mbox{i}\alpha\omega\Delta t(1 -\mbox{i}\omega\Delta t) ,\\&= \mbox{i}\alpha\omega\Delta t\left\{1+(1 -\mbox{i}\omega\Delta t) \right\},\\&= \mbox{i}\alpha\omega\Delta t\frac{1-(1 -\mbox{i}\omega\Delta t)^2}{1-(1 -\mbox{i}\omega\Delta t)},\\&= \alpha\{1-(1 -\mbox{i}\omega\Delta t)^2\}\\\vdots\\V[n] &= \mbox{i}\alpha\omega\Delta t +V[n-1](1 -\mbox{i}\omega\Delta t) ,\\ &= \mbox{i}\alpha\omega\Delta t\left\{1+(1 -\mbox{i}\omega\Delta t) +\ldots+(1 -\mbox{i}\omega\Delta t)^{n-1} \right\},\\&= \mbox{i}\alpha\omega\Delta t\frac{1-(1 -\mbox{i}\omega\Delta t)^{n}}{1-(1 -\mbox{i}\omega\Delta t)},\\&= \alpha\{1-(1 -\mbox{i}\omega\Delta t)^n\},](http://hooktail.maxwell.jp/bbslog/5b58aca2cab8fce446bacd563e6e2110.png)
と表現出来る.ここで,複素数「 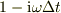 」で
」で  が十分小さければ,
が十分小さければ,
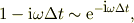
になるので,速度配列は;
![V[n] &= \alpha \{ 1-(1 -\mbox{i}\omega\Delta t)^n \},\\&= \alpha \left\{ 1-\left(\mbox{e}^{-\mbox{i}\omega\Delta t}\right)^n \right\},\\&= \alpha \left\{ 1-\mbox{e}^{-\mbox{i}\omega\Delta t \times n} \right\},\\&= \alpha \left(1- \mbox{e}^{-\mbox{i}\omega t_n}\right). \tag{e}](http://hooktail.maxwell.jp/bbslog/3fcc446152b3bcd4d570743408b2360a.png)
結局,式(d2)に示されているように,離散時間が進むごとに,y軸方向の力積成分, 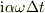 が新たに加算されるものの,前回の速度
が新たに加算されるものの,前回の速度 ](http://hooktail.maxwell.jp/bbslog/773c99455ee0de1925e07298a7f2bd26.png) のローレンツ力による微小回転と足し合わされたとき,公比,
のローレンツ力による微小回転と足し合わされたとき,公比, 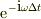 の組み合わせの妙で,時計方向に90度回転するらしい.その結果,
の組み合わせの妙で,時計方向に90度回転するらしい.その結果,
・横方向(+y方向)に速さ,αのドリフト運動を(仕事の基はy方向の力)生じ, ・他方,速度の大きさがαの時計方向の回転が生じている. ・当たり前の事ですが,磁場は仕事をしていませんね.
いやはや,ローレンツ力は,常識とちょっとずれている所が面白いものなのでしょう.例の「8の字リング」の水平移動モデルにも真似をした解析が出来ると愉快でしょうね.
Re: 平行板コンデンサー
zoro さんのレス (2007/07/20(Fri) 23:16)
速度の複素数表現は,前回の式(e)から,戻せば,
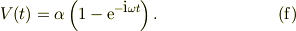
位置の複素数表現は,この式を時間で直接積分し,t=0で原点の解とすれば,
![R(t) &= \int_0^t V(t)\mbox{d}t, \\&= \alpha\left( t -\frac{\mbox{e}^{-\mbox{i}\omega t} -1}{-\mbox{i}\omega}\right), \\&= \frac{\alpha}{\omega}\left[ \{\omega t -\sin(\omega t)\} + \{1 -\cos(\omega t)\} \mbox{i} \right], \tag{g}](http://hooktail.maxwell.jp/bbslog/dc03eae17d8d748203731c7a6c6eee76.png)
となり,次のサイトの曲線と比較すれば,
確かにサイクロイドに一致します.
