サンダーＳＰ さんの書込 (2007/07/01(Sun) 17:45)

約１１ヶ月ぶりの久々の投稿質問かと思います． 弘前大学０５年第６問についてですが，結構悩んでおります．

以下，問題の問い方は幾らか変えました． (1)(b)熱とは内部エネルギーのことである解答：×（内部エネルギーは物体そのものの物理量，熱は移動する物理量） まずこれですが，自分はこれを○としました．しかし解答の理由についても，確かに熱はｄＱではなくｄ'Ｑと表す事が多いことからも納得がいきます．

一方で○とした理由ですが，熱力学第１法則ｄ'Ｑ＝ｄＵーｄ'Ｗが成立し，これは熱も，内部エネルギーも，仕事も全てエネルギーに変わりないという事を表していると解釈できます．（と思います．）つまり移動とか関係無しに，単なるエネルギー量として共に扱っているので別段区別する必要はないのではないか，という事です．（補足として付け加えると，熱そのものと，熱の流れは別物） さらにミクロに視点を移せば，内部エネルギーも熱エネルギーも共に分子のエネルギー（位置エネルギーも含む）にすぎず，熱エネルギーを運ぶには何らかの媒介（主に気体分子）が必要であり，その集まり自体に内部エネルギーを定義する事は可能ではないでしょうか？

しかも上の理由付けを正しくする（？）ような問いとして， (6)mv^2/2=3RT/2N0から１つの分子の温度が定義可能か？解答：できる（ＴをＵから求める） というのがあります． ちなみにこれは温度の定義みたいなものから納得がいきます．

最後に， (7)v~(分子の速さの平均)の算出法について述べよ解答：v=∫vf(v)dv(fは個数を表す) １個１個の分子の速さは測定できないので，納得がいきません．自分はこれを平均の量なので，観測可能な物理量Ｔ，Ｍと定数Ｒを使えば求まるとしました．第一，物理で積分不要の受験生にこういう聞き方はしないと思い，それを踏まえてこう考えました．また，解答では前提としてマクスウェル分布を考えていました．

自分は熱力学に関しては詳しい本を持っていないので，はっきりした定義なんかが分かりませんが，一応幾らか調べて，上のように考えました．（もし，手元に１冊あればよいという本があれば教えてください．） 多少説明が分かりにくいのかもしれませんが，何か指摘していただけると嬉しいです．お願いします．

サンダーＳＰ さんのレス (2007/07/05(Thu) 23:47)

このまま放って置かれるのは，やはり腑に落ちないので，もう一度上げさせていただきます． 恐らく僕の説明が悪いからだとは思いますが，どうかこれに関してお願いします．少しでも熱力学を理解したいので．

toorisugari no Hiro さんのレス (2007/07/05(Thu) 23:55)

> 確かに熱はｄＱではなくｄ'Ｑと表す事が多いことからも納得がいきます．

この違いの意味はご理解されているのでしょうか? また，エントロピーについてはどれだけご理解されているのでしょうか?

サンダーＳＰ さんのレス (2007/07/06(Fri) 00:41)

＞この違いの意味はご理解されているのでしょうか?

dUやdTというのは，dU=CvdTすなわちdU/dT=Cvのように，微分にまつわる量みたいなもので，ＵやＴ自体がパラメータとして状態を表すものであり，d'Qは単なる微小変化で，これ自体状態のパラメータとはならない量だという風に一応理解しておりますが．（もしかしたら間違っていますか？）

＞また，エントロピーについてはどれだけご理解されているのでしょうか?

微妙ですが，よく言われる乱雑さだと，熱力学とのイメージが合わないので，熱力学における位置エネルギーっぽいものと勝手に解釈しています．抵抗≒不可逆過程で，ある一定の力学的エネルギーが実現可能な運動を表すパラメータの動く領域が決まっている（単振動なら運動量と位置を変数とする位相空間内で一定の楕円軌道を描く）ように，エントロピーでも，それが一定なら同様の事が言える（この場合２変数が自由だから曲面？），という風に考えておりますが． ただ結構機械的に処理できるのであまり詳しく追究した事がありません．

前者のほうは何かの本で書いてあったと思うのですが，後者は完全に自分の考えです． 間違っていたらもう一度きちんと勉強しなおします．

クロメル さんのレス (2007/07/06(Fri) 00:43)

全問答えられなくてすみません． ひとつだけ気になったので，思い出したので書いてみます． 指導要領がかわってしまっているかもしれませんけど，

(7)についてですが，高校の教科書に，

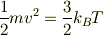
というような式がありませんでしたか？ 二乗平均速度とかがキーワードだとおもいます．

zoro さんのレス (2007/07/06(Fri) 18:16)

サンダーＳＰさん，多面的に勉強されていますね．

私は，大昔に「熱力学を捨てた」ので，意見する事は出来ません．

ただこのスレッドを拝見していて，昨日，近くの図書館を見ていたら，新刊の書で；

熱力学の基礎， 清水 明・著， 東京大学出版会，2007-03 ISBN13: 978-4-13-062609-5 pp408

これは，受験用の本では在りませんが，サンダーＳＰさんの数学力なら，結構な所まで読めるかも知れません．

一度，本屋さんで； ・p iii， まえがき ・p v，本書の読み方 ・p２２, 注意 をご自分の目で見られると面白いです．

p16には，この本特有のヴェクタやナブラの表示が在ります．これを見て，この本をすこし読み始めました．そんなミーハーな読者ですが，本格的に読みたくなりました．

私の意見としては，大学1年生のときに，他の講義と平行して，味わいながら読み下していくのが良いようにも感じました．

なお，この掲示板では，この本の参考文献にもある；

[6] 田崎 晴明『熱力学 ー 現代的な視点から』(培風館)

が一押しだと思いました．この筆者は，統計力学の本も近く出版されるとか．

〜〜〜 いずれにしても，熱力学の関係に詳しい方々からの助言をお願いしたいですね．

サンダーＳＰ さんのレス (2007/07/07(Sat) 18:45)

クロメル様へ

(7)については，その関係式を変形し，k(ボルツマン定数)=R/Na(R:気体定数，Na:アボガドロ定数)を代入し，それで僕は求まると考えたわけです．（原子１個の質量は簡単に観測できるとは言い難いので）

ただ分からないのは，問題が気体分子がばらばらに異なる速さで動いているので，その２乗平均速度を求めるのは一つ一つ測定する必要がある，みたいな事を書いていて，分布関数を積分して求めていくという確率の期待値に似た方法が答えとなっているのが少し気に入らないわけです．その分布関数自体理論から導き出しているので，自分はその(運動エネルギー)=3kT/2の方をただ使っただけです．（大半の受験生が普通にたどる方法だと思います）

zoro様へ

ありがとうございます． 両方ともお目にかかった事が無いので内容は分かりませんが，アマゾンとかで見ているとすごく読んでみたい気になりました． 前者のほうは，これと同じ著者の別の本をちょうど持っていまして，なかなか良かったので，本屋にあれば買おうかなとも思います． 後者は，市内の図書館にあるようなので，そこで一度借りてみます．

クロメル さんのレス (2007/07/07(Sat) 20:11)

なるほど，解答というのは，本に書いてあった正しいとされる答えですか．

受験生相手に（確率）分布関数を要求するのは，ちょっとレベルが高すぎる気がします． それに定義ではなく，算出法とかいてあるので，どうやって計算するか例を出せ と読めなくもありません． 文脈がわからないと，なんともいえませんが，突然分布関数をださせるような 問題なら，悪問だと思います． サンダーＳＰさんの答えでも合っているといいたいですね．

ついでに，(1)(b)については，熱力学において熱という概念と内部エネルギーという概念は，

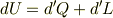
を考えれば，違う概念であるというべきだと思います．

確かに外に仕事をしない時（ｄ’Ｌ＝０）は，加えていったエネルギーは，内部エネルギーですけどね．

zoro さんのレス (2007/07/07(Sat) 22:23)

論議に，直接的に関与出来ませんが，茶々を入れさせて下さい．

数十年前の自分には； 「熱の物理的イメージが判らなかった！」 のが，敗因でした．

例えば，気体分子運動論で考えれば，気体分子の衝突課程に統計的な分布仮定を付与して論議が進むので，それなりに興味が涌きました．

ところが，「熱」という意味は，「容器の熱的振動」を媒介にした容器の内部と外部の気体間の運動エネルギの伝達としてしかイメージ出来なくて，挫折しました．

〜〜〜

＞なるほど，解答というのは，本に書いてあった正しいとされる答えですか．

若し宜しければ，その本をご紹介いただけますか？

恐らく，この掲示板では《市場に出回っている本」を基に，論議がなされるのは問題ない》と私は思います．

yama さんのレス (2007/07/08(Sun) 13:20)

ちょっと気になる点について述べておきます．

>一方で○とした理由ですが，熱力学第１法則ｄ'Ｑ＝ｄＵーｄ'Ｗが成立し，これは熱も，内部エネルギーも，仕事も全てエネルギーに変わりないという事を表していると解釈できます．（と思います．）つまり移動とか関係無しに，単なるエネルギー量として共に扱っているので別段区別する必要はないのではないか，という事です．（補足として付け加えると，熱そのものと，熱の流れは別物）

ｄ'Ｑ＝ｄＵーｄ'Ｗは，内部エネルギーの変化についての関係式であって，内部エネルギーそれ自体についての式ではありません． エネルギーの移動によって内部エネルギーが変化するわけですが，その場合のエネルギーの移動の形が熱や仕事であって，移動に関係なしに熱や仕事を考えることはできません．つまり，熱は移動に無関係な単なるエネルギー量として扱われているわけではありません．

>mv^2/2=3RT/2N0から１つの分子の温度が定義可能か？解答：できる（ＴをＵから求める）

mv^2/2=3RT/2N0によって１つの分子の温度が定義できなくはないと思いますが，その場合は温度が純粋に力学的に定義されることになり，そのように定義された温度は，熱力学や統計力学で考えられる温度とは異なったものになってしまいます． 普通は，温度は多数の粒子からなる系の状態を巨視的に特徴づける物理量であって，熱力学や統計力学に固有のものだと思います． そもそも mv^2/2=3RT/2N0 は，多数の分子からなる系において分子１個当たりの平均の運動エネルギーについて成り立つ関係式であって，特定の１つの分子について成り立つ式ではありません．

サンダーＳＰ さんのレス (2007/07/09(Mon) 00:49)

>受験生相手に（確率）分布関数を要求するのは，ちょっとレベルが高すぎる気がします． それに定義ではなく，算出法とかいてあるので，どうやって計算するか例を出せ と読めなくもありません． 文脈がわからないと，なんともいえませんが，突然分布関数をださせるような 問題なら，悪問だと思います．

>若し宜しければ，その本をご紹介いただけますか？

問題自体が分布関数については触れられておらず，その積分自体が解答となっているわけです． ただ大学側はそこまで要求せず，本の編集者がそう書いたのかもしれません． ちなみに本というのは，旺文社の全国大学入試問題集の昨年版ですので，今は恐らく出回っていないはずです．（僕は学校の図書館にあったのでやったわけです）

>ｄ'Ｑ＝ｄＵーｄ'Ｗは，内部エネルギーの変化についての関係式であって，内部エネルギーそれ自体についての式ではありません． エネルギーの移動によって内部エネルギーが変化するわけですが，その場合のエネルギーの移動の形が熱や仕事であって，移動に関係なしに熱や仕事を考えることはできません．つまり，熱は移動に無関係な単なるエネルギー量として扱われているわけではありません．

つまり内部エネルギーの移動があって初めて熱や仕事について論じる事が可能で，その変化の原因となるエネルギー自体を熱と呼んでいるという事でしょうか？ 混同しているのは多分，自分の中では，熱も内部Ｅも分子のエネルギーというような概念が定着しつつあるからだと思います．

>mv^2/2=3RT/2N0によって１つの分子の温度が定義できなくはないと思いますが，その場合は温度が純粋に力学的に定義されることになり，そのように定義された温度は，熱力学や統計力学で考えられる温度とは異なったものになってしまいます． 普通は，温度は多数の粒子からなる系の状態を巨視的に特徴づける物理量であって，熱力学や統計力学に固有のものだと思います． そもそも mv^2/2=3RT/2N0 は，多数の分子からなる系において分子１個当たりの平均の運動エネルギーについて成り立つ関係式であって，特定の１つの分子について成り立つ式ではありません．

一つ付け加えておきますと，問題右の解答というのは問題集の解答です． このあたりについては結構考えましたし，わかっているつもりです．だから最初×としていまして，解答見た後，あれっと思い，温度について調べてみると，他の物理的性質から決定される示量としての物理量と書いてあったので，可能だと思いました． あくまで温度が巨視的にみて初めて意味をなす事は分かっています．刻々と運動が変化するに分子に温度を定義しても，何の役にも立たないですよね．

zoro さんのレス (2007/07/09(Mon) 02:34)

＞本というのは，旺文社の全国大学入試問題集の昨年版ですので，今は恐らく出回っていないはずです．（僕は学校の図書館にあったのでやったわけです）

なるほど，漸く高校の物理の範疇である事を理解しました．手元に出ていた数研出版の2007年度，物理?の「第3編物質と原子第1章熱と物質の状態２気体の法則と気体分子の運動」を拝見しました．

分子運動論もどきがちらっと出てくるものの，これが物理の本の説明かと思う位，悲しい説明で，いっそのことこんな説明は端折っても，ちっとも問題ないと思いました．

逆にいえば，確かにご質問の出題は，高校の範囲を逸脱した，とんでもない出題であり，受験生の皆さんに対してアンフェアな出題だと思います．

でも，サンダーＳＰさんの疑問ももっともと思うので，熱力学に造詣の深い方からの直裁な解説を切望します．

toorisugari no Hiro さんのレス (2007/07/09(Mon) 14:17)

> つまり内部エネルギーの移動があって初めて熱や仕事について論じる事が可能で，その変化の原因となるエネルギー自体を熱と呼んでいるという事でしょうか？ > 混同しているのは多分，自分の中では，熱も内部Ｅも分子のエネルギーというような概念が定着しつつあるからだと思います．

まず，マクロ(巨視的)な学問である熱力学を考えるときは，ミクロ(微視的)な分子のことは忘れてください．(分子動力学，あるいは統計力学と熱力学は別の学問です．)

現実の気体はアボガドロ数相当( 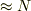)個の分子が位置や速度を刻一刻変えながら構成しています．ですからある時刻の気体の状態を記述するには 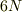個の変数( 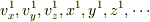)で記述しないといけません．

しかし，気体を観測していると，少数の物理量(温度や圧力など)だけで状態が指定できることが「経験的」にわかっています．この経験をまとめたものが熱力学です．(決して，分子の知識は使っていません．)

熱力学では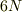， 次元の空間の一点として記述すべきものが，2次元かそこらで記述できるのです．なぜこのように気体が少数の変数で記述できるかを，熱力学では答えていません．たんに，「世界がそうなっている」のをまとめただけです．

このような少数の変数で記述できる量を状態量と言います．この「状態量」という考えが熱力学では重要なのです．

状態量(例えば内部エネルギー )の変化は 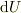で表されますが，これは 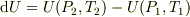の様に状態量の引き算で表されます．このような 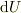といったタイプの微少量を「全微分」といいます．

しかし，すべての微小変化が状態量の差，つまり，全微分，で表されるわけではありません．

特に，熱 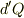は変化の始点終点だけでなく経路にも依存するので，引き算では記述できません．全微分ではありません．ですから，状態量 を考えることはできないのです．(分子すべての位置と速度を変数と考えれば，状態量と考えることもできるかもしれません．でも，それは熱力学ではないです．)

乱暴なアナロジーですが，サンダーＳＰさんが考えておられるのは，「物質は分子でできていて，分子の位置エネルギーや運動エネルギーですべて表現できるはずだと」という信念もとに，(保存力ではない)摩擦力の「位置エネルギー」を，マクロな理論である古典力学の枠組みの中で導き出そうとされているようなものです．

マクロとミクロの間には大きな溝があるのです．

俊一 さんのレス (2007/07/09(Mon) 21:31)

とても，議論が広がってしまっているのですが僕は出題も解答も適当なものだと考えます． 物理でいう熱という言葉は，日常用語の熱とは別物です．物理でいう熱とはエネルギーの流れのうちで，力学的なマクロの形のエネルギーの流れ以外のものをいう．はっきり言えば，ミクロレベルの分子運動によるエネルギーの流れです．物理では仕事と運動エネルギーを区別するように，熱と内部エネルギーを区別します． 議論の前に言葉の定義を明確にする必要があろうかと思いますし，出題者もそのことを試そうとしていると思います

サンダーＳＰ さんのレス (2007/07/09(Mon) 23:22)

皆様ありがとうございます．かなり分かってきた気がします． 恐らくは分子運動論から勉強してしまったために，熱力学と分子運動論をかなり混同してしまっていたようです．（そのために当初，内部Ｅが何なのか飲み込めず，知らないうちに分子の運動と関連付けてしまったみたいです．）

結局，熱力学と統計力学を同じ現象を全く別の観点から捉えただけで，基本は別分野ときっぱりと割り切り，

熱力学／統計・運動論 内部Ｅ／力学的Ｅ 圧力（という示強的物理量）／分子の衝突 蒸発（という現象）／分子の結合がきれ，飛び出す 温度／定義できるが無意味 Ｓは他の物理量から定まる示強変数／散らばり具合で定まる物理量

みたいに，考えた方がよいのでしょうか．（分子の存在を信じなかった当時の物理学者たちが考えていた熱現象のように）

ただやはり問題にも落ち度が無くもない気がします．もう一度その問題文を見直しましたが，どこまで同じと見るか人によって違いますし，例えば，単にエネルギーと質量は等価だとして基本同じものと捉える人もいると思います．（常識で考えれば，こういう設問では熱と内部Ｅを違うものと捉えるべきなのかもしれませんが．）

これを機にもう一度熱力学全体を捉えなおそうかなと思います．（そうすれば以前投げ出した相転移とかがもしかすればきちんと理解できるかもしれない）

eco さんのレス (2007/07/12(Thu) 18:09)

この入試問題

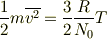
に基づいて，１つの分子の温度というものを定義できますか．また，その理由は何ですか．50字以内で答えなさい．

に対する，赤本（教学社）の解説では，

いいえ理由：気体分子の運動エネルギーは絶対温度に比例するが，温度の定義とは別であるから．

とあり，旺文社の解答と異なっています．

いいえの理由については，よく飲み込めていません． 理由は，やはり，yamaさんの >そもそも mv^2/2=3RT/2N0 は，多数の分子からなる系において分子１個当たりの平均の運動エネルギーについて成り立つ関係式であって，特定の１つの分子について成り立つ式ではありません． という指摘のとおりだと思います．

zoro さんのレス (2007/07/12(Thu) 21:46)

ecoさん，初めまして．

ああ，平均の記号が付いているなら，少しはホッとします； ．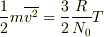

しかし，「ある市販の高校の教科書」を拝見すると，平面に対する正面衝突の力積を計算した後に，分布関数の話は一切，省略されて，「PV」の右辺に平均値が出て来て，ボイル・シャルルの式との比較から，運動エネルギの平均値との関係を出すようです．

＃此れでは，統計力学の役割と熱力学の役割が，中途半端に対応付けをされて，柔らかな分子運動(分子相互の振動や回転)とkT/2との関係が見えにくくなると感じます． ＃その上，統計力学的な計算で温度がいとも簡単に定義されるかのような，誤解を受けると思います．

自分のように，要領の悪かった学生は，点でチンプンカンプンです．こうゆう風に「奇策を労してまで教える事は無い」と思ってしまいます．どうしても書きたいならば，「化学の高校の教科書のコラム」にでも書くべきではないでしょうか？

百歩ゆずって，熱力学と偏微分の性質を丁寧に教える方が，宜しいと思います．

でも，自分の意見は， ・熱力学は，一年次の前期ないし後期にに自習をしてもらい， ・さらに，熱力学は1年次の後期ないし，2年時の前期で講義とする． ・統計力学は；大学の2年次の前期・後期ぐらいの日程でキッチリと教える． といった日程で教えないと，身に付いた理解が得られない？

と書くと，「軟弱！」といった批判がでて来るようですね．

サンダーＳＰ さんのレス (2007/07/12(Thu) 23:08)

この議論はもう終わったと思ってましたが，やはり気になるので少し．

この問題について一度前に調べたとき，温度は他の物理量によって定まる量とある本に書いてあったので，分子にも温度が定義可能なんだと一応納得しました．（既述のように自分は最初，いいえとして，答えが定義可能となっていたので悩みました．）

でも少し気になって調べた所，Wikipediaでは， 『平衡状態における分子の運動エネルギーを，エントロピーという統計値で微分したものである』 となっているので，少なくともエントロピーという統計的な量が必要であるため，分子単独ではやはり定義できないみたいです．（そもそも分子一つでは，平衡状態自体存在しないですよね？）