２足歩行ロボの転倒

ろぼさんの書込 (2007/07/01(Sun) 17:15)

はじめまして．

コンピューター上で，２足歩行ロボの挙動をシミュレートしてみようと思い，物理を勉強し始めた初心者です．

頭，胴体，対になった２の腕，腕，モモ，足（すね）に同じ質量の質点があるロボについて，片方の腕や足を取り除き，重心がずれた時の転倒を再現しようとしたのですが，片足立ちでバランスを失った時のように徐々に傾いていかず，コテっと倒れてしまいます．傾きの計算は以下の通りです．

ｘ軸は右が正方向の横軸とし，ｙ軸は上が正方向の縦軸としてｘｙ平面で考えています．

まず各パーツのｘｙ座標と質量の積の全ての和から重心と，ロボの中心から重心までの距離ｒを求めます．そしてロボの総質量とｒの積から転倒モーメントを，足の長さと総質量から抵抗モーメントを求め，転倒モーメントから抵抗モーメントを引いて，値が負になった場合，その値をトルクのｙ成分とし，トルクのｘ成分を

√トルクｙ×トルクｙ＋ｒ×ｒ

と求め，トルクのｘｙ成分を用いたアークタンジェントから角度を求め，その角度をロボのｚ軸回転値に加算していき転倒の傾きを再現しようと思ったのですが…

かなりデタラメな計算をしていると思いますが，よろしければ間違いの指摘，アドバイスなど頂ければ幸いです．

長文，失礼しました．

はじめまして，ろぼさん．おもしろそうなことをされてますね．最初は回転がゆっくりでなければならないということですか？おそらく回転の運動方程式や慣性モーメントを考慮していないからではないでしょうか？

お聞きします限り，

>その値をトルクのｙ成分とし，トルクのｘ成分を √トルクｙ×トルクｙ＋ｒ×ｒと求め，トルクのｘｙ成分を用いたアークタンジェントから角度を求め，その角度をロボのｚ軸回転値に加算していき転倒の傾きを再現しようと思ったのですが…

あたりが，怪しい気がしますね．

重心周りのxy平面内の慣性モーメントをI_zとし，（これがなにかご存じなかったら，詳しくは私の書いた記事を参照してもらえますか？面倒だったら適当な定数で結構です．大きさの目安は，（全質量）×（重心から足の先までの長さ）＾２です．）

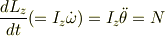
$\frac{dL_z}{dt}(=I_z \dot{\omega})=I_z\ddot{\theta} = N$

Nのトルクはろぼさんが求めたものでよさそうです．ここで，注目していただきたいのは回転角θは，二回微分が増加していくということです．

角速度ω += ω + トルク×（微少時間）とし，回転角θ += θ ＋ ω×（微少時間）なんておけばいいんじゃないかなと思うのですが．

お返事，ありがとうございます！

直ぐには理解でいきないと思い，まず，お礼のお返事をさせていただくことにしました．

慣性モーメント…物体の回りにくさってモノがあるのですね．

ではでは．

いえいえ，

一度わかってしまうと簡単なことだと思いますけどね．老婆心ながら補足しておくと，

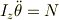
$I_z \ddot{\theta} = N$

だけが，本質です．(Iはただの定数)

ろぼさんは回転角にトルクを加えていくという，いわば，

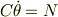
$C\dot{\theta}=N$

のようなモデルを立てましたが，実際は 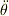$\ddot{\theta}$ で考えなければならないということです．

EMANさんのページにこんなことが書いてありましたよ．参考まで．