力学

力学

jin さんの書込 (2007/06/27(Wed) 16:11)

次の問題の解説をお願いします．

[1]a=(Ａx,Ａy,Ａz)，b=(Ｂx,Ｂy,Ｂz)，c=(Ｃx,Ｃy,Ｃz)のベクトルがある．
このベクトルにa+b=cかつＡ＋Ｂ＝Ｃが成り立つとき，aとbがお互いに 平行になることを，ベクトル積の性質を利用して証明せよ．
[2]xy平面内で，x=acosθ，y=bsinθ，θ=ωt(a,bは定数でa≠b)にしたがって
運動する質点Pについて以下の設問に答えよ．

(1)Pの描く軌道の方程式を求め，この軌道はどのような形になるか述べよ． (2)Pの速さを求めよ． (3)Pの加速度の大きさを求めよ． (4)Pの運動の原点ОからPへの動径方向の加速度成分とそれと直角の方向の

加速度成分を求めよ．

よろしくお願いします．早めにご回答頂ければ幸いです．

Re: 力学

zoro さんのレス (2007/06/27(Wed) 17:42)

物理の問題というより，数学の演習問題見たいですね．

[1]について

A=|a|というならば，ベクトルの条件式；a+b=c;を両辺を自乗(ベクトルの内積)して，c^2=C^2をA,Bで書き直してみるとどうですか？

[2]について

x，yは，θ=ωtとい媒介変数を通して変化するのだから，例えば，x方向の速度は；

vx(t) = dx/dt = dx/dθ * dθ/dt = a(dcos(θ)/dθ)*(d(ωt)/dt) = -aωsinθ(t)

のに注意すれば，他も同様に微分できますね．

力学

jin さんのレス (2007/06/27(Wed) 21:51)

おっしゃる通り途中までやってみたんですが・・・ やはり自分の力量では少し解けそうにありません． 完璧な回答をお願いしたいのですが・・・． できれば解説もお願いします．色々とすみませんｍ（_ _）ｍ

Re: 力学

zoro さんのレス (2007/06/27(Wed) 22:41)

途中までやった所を書かないで，一方的に完全回答を求められるのは，質疑応答の公平性に欠けると思います．

単に完全回答が欲しいのならば，他の掲示板で質問された方が良いのではないでしょうか？

【追伸】

もし，現在，理工系の分野の学校で勉強されているとすれば，この問題の前後は，是非とも確実に理解される事をお勧めします．もし，その勉強の中で，理解に苦しむ所があれば，出来るところまで論議させていただきます．

他方，文科系で，勉強されている場合で，こんな分野はどう考えても関係ないのに，という場合で，試験に合格する為と，割り切るばあい，他の掲示板のほうが速いと思います．

というのも，20世紀での爆発的な科学技術の発達を受けて，一人が学ぶべき事柄が増大しています．必ずしも，全ての分野を等しく学ぶ事は困難になっています．

ですから，勉強する時も，巧く取捨選択する必要があると思います．このとき，「全てを学ばない」という場合でも，例えば，文科系の分野の中核となる部分は，我々も学ぶべきでしょう．しかしそのエッセンスで良いと思います．

同様に，文科系のかたも，理工系のエッセンスを学ぶにしても，細かな定量性を含む部分は省略してもよいのではないかと思うからです．

力学

jin さんのレス (2007/06/28(Thu) 22:43)

返信遅れてすみません． なんとか[2]の(3)まで解けましたが，最後の(4)はどんなに考えても 解けそうにありません．ヒントをお願いします．

Re: 力学

zoro さんのレス (2007/06/28(Thu) 23:33)

では，[2]の(2),(3)の答えを記入して下さい．それがデカルト座標系での速度と加速度の表式になります．

とすれば，後は，デカルト座標(x,y)の組を極座標(r,θ)の組に変換するだけの事です．と言うのだけは簡単ですが，講義で，この話はされたのですよね？簡単に復習すれば，

<pre> +y軸

\vec e_y ↑ \vec e_{\theta}\quad \vec e_{r}
｜ \nwarrow\nearrow
Y・ーーーーーー・P

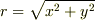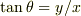｜／｜ ｜／｜ r=\sqrt{x^2+y^2} ｜r ／｜ \tan{\theta}=y/x ｜／｜ ｜／｜ ｜／ \theta ｜ ＋ーーーーーー・ーーー→ +x軸

O X \vec e_x

</pre>

座標原点Oから点Pの位置ヴェクタを考えている訳で，

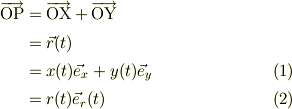
\overrightarrow{\mathrm{OP}} &= \overrightarrow{\mathrm{OX}} +\overrightarrow{\mathrm{OY}}\\ &= \vec r(t)\\&= x(t)\vec e_x +y(t)\vec e_y \tag{1}\\&= r(t) \vec e_{r}(t) \tag{2}

式(1)は，平面でのデカルト座標は，2つの正規直交基底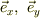，（ \vec e_x,\ \vec e_y ）で表せるわけですね．

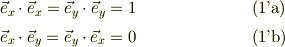
\vec e_x \cdot \vec e_x = \vec e_y \cdot \vec e_y = 1 \tag{1'a}\\\vec e_x \cdot \vec e_y = \vec e_y \cdot \vec e_x = 0 \tag{1'b}

当たり前ですが，これらの正規直交基底は，座標値xなり，yなりが一定の面に垂直で，かつ，その座標値が増加する方向を向いています．

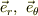同様に，xy平面での極座標でも，座標値 r なり， \theta なりが一定の面に垂直で，かつ，その座標値が増加する方向を向いるように正規直交基底，（ \vec e_r,\ \vec e_{\theta} ）を考えれば良い事になります．

上の図から明らかの様に； ・動径方向の単位ヴェクタ 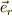\vec e_r ・接線方向の単位ヴェクタ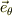 \vec e_{\theta}

が基底ヴェクタとなりますが，幾何学的関係から，

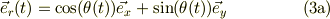
\vec e_r(t) &= \cos(\theta(t))\vec e_x + \sin(\theta(t))\vec e_y \tag{3a}

接線方向の単位ヴェクタ 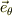\vec e_{\theta} は，動径方向の単位ヴェクタ 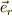\vec e_r を90度，反時計方向に回転したものですから；

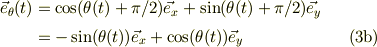
\vec e_{\theta}(t) &= \cos(\theta(t)+\pi/2)\vec e_x + \sin(\theta(t)+\pi/2)\vec e_y\\&= -\sin(\theta(t))\vec e_x + \cos(\theta(t))\vec e_y \tag{3b}

と表す事が出来ますね．これを見易く行列表示にすると；

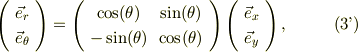
\left( \begin{array}{cc} \vec e_{r}\\ \vec e_{\theta}\\ \end{array} \right) = \left(\begin{array}{cc} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta)\\ \end{array} \right) \left( \begin{array}{cc} \vec e_{x}\\ \vec e_{y}\\ \end{array} \right), \tag{3'}

と書く事が出来ます．ここで，2次元の回転行列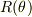， R(\theta) として，

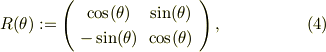
R(\theta) :=\left(\begin{array}{cc} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta)\\ \end{array} \right), \tag{4}

と定義すると，式(3')もコンパクトに表す事が出来る；

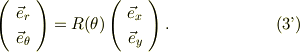
\left( \begin{array}{cc} \vec e_{r}\\ \vec e_{\theta}\\ \end{array} \right) = R(\theta) \left( \begin{array}{cc} \vec e_{x}\\ \vec e_{y}\\ \end{array} \right). \tag{3'}

そこで，式(3')の辺々に 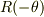R(-\theta) を作用させると；

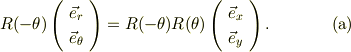
R(-\theta)\left( \begin{array}{cc} \vec e_{r}\\ \vec e_{\theta}\\ \end{array} \right) = R(-\theta)R(\theta) \left( \begin{array}{cc} \vec e_{x}\\ \vec e_{y}\\ \end{array} \right). \tag{a}

ここで，回転行列の性格から，ある角度回転して，同じ角度を逆回転するのは，何も回転しないことだから，

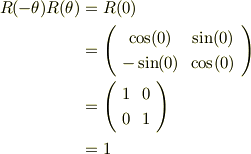
R(-\theta)R(\theta) &= R(0) \\&= \left(\begin{array}{cc} \cos(0) & \sin(0) \\ -\sin(0) & \cos(0)\\ \end{array} \right) \\&= \left(\begin{array}{cc} 1 & 0 \\ 0 & 1\\ \end{array} \right) \\&= 1

従って，式(a)は，

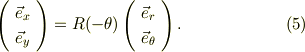
\left( \begin{array}{cc} \vec e_{x}\\ \vec e_{y}\\ \end{array} \right) = R(-\theta)\left( \begin{array}{cc} \vec e_{r}\\ \vec e_{\theta}\\ \end{array} \right). \tag{5}

となります．この周辺の算術には，実用的にも，理論的にも大切な性質が沢山あるので，ヴェクタ解析，線形代数などの参考書をご覧になって」下さい．

速度についても，デカルト座標と極座標の単位ヴェクタで表す事が出来て；

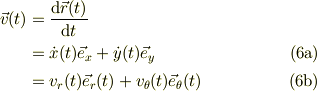
\vec v(t) &= \frac{\mbox{d} \vec r(t)}{\mbox{d} t}\\&= \dot x(t)\vec e_x + \dot y(t)\vec e_y \tag{6a}\\&= v_{r}(t)\vec e_{r}(t) +v_{\theta}(t)\vec e_{\theta}(t) \tag{6b}

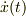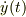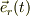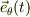ここで，式(6a}の係数， \dot x(t) と \dot y(t) はお求めになった訳ですから，既知です．他方，式(6b)の係数を求めるには，式(6a)と式(6b)とに， \vec e_{r}(t) や \vec e_{\theta}(t) との内積を作り，さらに式(3a,b)を用いれば， ；

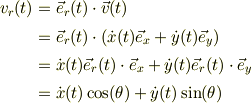
v_{r}(t) &= \vec e_{r}(t)\cdot \vec v(t)\\&= \vec e_{r}(t)\cdot \left(\dot x(t)\vec e_x + \dot y(t)\vec e_y \right) \\&= \dot x(t)\vec e_{r}(t)\cdot \vec e_x +\dot y(t)\vec e_{r}(t)\cdot \vec e_y\\&= \dot x(t)\cos(\theta) +\dot y(t)\sin(\theta)

同様に

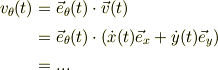
v_{\theta}(t) &= \vec e_{\theta}(t)\cdot \vec v(t)\\&= \vec e_{\theta}(t)\cdot \left(\dot x(t)\vec e_x + \dot y(t)\vec e_y \right) \\&= ...

となります．

加速度も同じ流れで，計算出来ますね．この手の計算は，今頃，何度か手計算に慣れておくと，段々スマートな方法をマスタする時にその有難さが身に沁みるので，一度は自分で鉛筆(ないしはキーボード)により計算する事をお勧めします．

でも余り，ナイーブな方法に拘り過ぎないことも重要です(笑)．あまり勤勉すぎるのも考えものであります．

＃しかし，ナイーブな方法は，必要に応じて計算出来る強みが在ります． ＃丁度，地震のような時に，役立つのは，文明の利器よりは，素朴なマッチやローソクのようなものなどと同じです． ＃高級な数学や，解析力学も大切ですが，その根底にある素朴な方法論を身につけた上でないと，解釈がひ弱になってしまうと思います．