RLC直列回路について

RLC直列回路について

こーへい さんの書込 (2007/06/26(Tue) 10:56)

RLC直列回路で，インピーダンスの大きさ|Z|はどのようになるのですか？

Re: RLC直列回路について

zoro さんのレス (2007/06/26(Tue) 13:00)

こーへいさん，初めまして．

どのような授業を受けられたか解らないので，解る範囲で書いてみます．

直列回路に電位 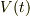V(t) が加わって，電流 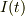I(t) が流れるとすれば，各素子ごとの電位を電流の関数としてあたえられます；

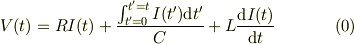
V(t) = RI(t) + \frac{\int_{t'=0}^{t'=t}I(t')\mbox{d}t'}{C} +L\frac{\mbox{d}I(t)}{\mbox{d} t} \tag{0}

なお，t=0まで，電位，電流ともゼロであったとします．

いまインピーダンスを考えるので，十分に定常的な場合(逆に言えば，初期条件で決まる状態は減衰してゼロとなっている)を考えます．そして入力の電圧が，一定の角速度 \omega の交流だとします；

V(t)=V_0\mbox{e}^{\mbox{i}\omega t} \tag{1}

直列回路を流れる電流も；

I(t)=I_0\mbox{e}^{\mbox{i}\omega t} \tag{2}

式(2)を式(0)の右辺に代入すると

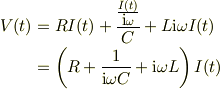
V(t) &= RI(t) + \frac{\frac{I(t)}{\mbox{i}\omega}}{C} +L\mbox{i}\omega I(t)\\&= \left( R + \frac{1}{\mbox{i}\omega C} +\mbox{i}\omega L \right)I(t)

インピーダンスZは，電圧に対する電流の比だから；

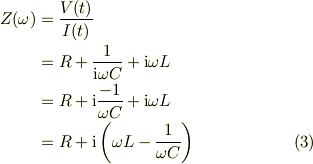
Z(\omega) &= \frac{V(t)}{I(t)} \\&= R + \frac{1}{\mbox{i}\omega C} +\mbox{i}\omega L\\&= R + \mbox{i}\frac{-1}{\omega C} +\mbox{i}\omega L\\&= R + \mbox{i}\left( \omega L -\frac{1}{\omega C} \right) \tag{3}

従って，

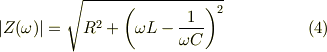
|Z(\omega)| = \sqrt{R^2 + \left( \omega L -\frac{1}{\omega C} \right)^2} \tag{4}

Re: RLC直列回路について

こーへい さんのレス (2007/06/26(Tue) 23:05)

zoroさん，丁寧にどうもありがとうございました．とても助かりました． 横軸をf，縦軸を|Z|のグラフを書きたかったんですよね....... でもこれで何とかなりそうです．本当にどうもありがとうございました．