比熱
比熱
ありす さんの書込 (2007/06/18(Mon) 22:55)
古典統計力学で『比熱の値は一定値になり温度変化しない』と結論付けられますが,絶対零度において比熱がなぜ0でなければならないでしょうか?
Re: 比熱
toorisugari no Hiro さんのレス (2007/06/19(Tue) 12:17)
> 絶対零度において比熱がなぜ0でなければならないでしょうか?
そもそも,絶対温度に何故下限(=零度)があるのでしょうね.どうして負の絶対温度がないのでしょうか?(実は「違うところに」存在しているのですが...).比熱が零度で0になることより,そちらが不思議だったりします.
ともかく,ここらへんは「熱力学の第3法則」というキーワードで勉強されることを おすすめします.
Re: 比熱
クロメル さんのレス (2007/06/20(Wed) 03:32)
温度の定義を考えればいいのではないでしょうか. つまり,比熱はエネルギーの温度微分ですから,温度の定義の仕方によって,性質が変わってくるということです.
ありすさんは状態数Ωはご存知ですか? 知っているという前提であれば話が早いです. 古典統計の話をしているならたぶんご存知(?)だと思うので 話を進めてみます.分からなかったら質問してください.
エネルギーをM個のエネルギー単位δの集まりと考えて,系のエネルギーEとして,E=Mδとします.それをN個の振動子に分配する方法は,
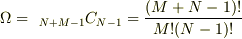 通りというのはいいですか?
通りというのはいいですか?
温度(かけるボルツマン定数k)の逆数は,状態数の対数を取ったもののエネルギー微分ですよね.つまり,  です.式(1)は温度の定義だと思ってかまいません.
です.式(1)は温度の定義だと思ってかまいません.
エネルギーをδだけ増やしたときの状態数の増分をδで割れば左辺をあらわせます. つまり,
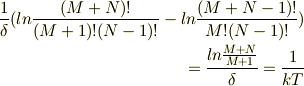
となります. ここで,デルタは振動子を励起するのに必要なエネルギーですから, 大きくともボルツマン定数よりも8桁くらい小さく10^{-31}くらいのようです. でも,δは振動子の最小励起エネルギー単位ですから,そんな数字なんかよりもずっと小さいのかもしれません. ( http://ja.wikipedia.org/wiki/%E6%95%B0%E9%87%8F%E3%81%AE%E6%AF%94%E8%BC%83_%28%E3%82%A8%E3%83%8D%E3%83%AB%E3%82%AE%E3%83%BC%29 参照)
ここで温度とエネルギーの関係が分かったので,やっと比熱が分かります.
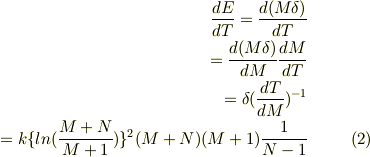
これはM=0でボルツマン定数(10の−23乗)ほどに小さく, Mの大きいところでは,M^2に比例する値です.
ちょっと意外な結果(私はδが小さくなればなるほど比熱も小さくなると思っていました.)になりましたが,これでTはゼロでボルツマン定数ほどに小さくなる ことが示せました.
すこし補足しておくと,温度の定義(状態数についての議論)はM〜1程度の小さいところまで考えていないと思います.つまり,我々が状態数を議論できるのは式(2)がM^2で小さくなっている高温部分だけなのだと思います.エネルギーの塊が数えられるくらいの低温極限は,人間が到達できるスケールをはるかに超えています.
他の方のご意見も聞きたいです.ご意見を歓迎します.
Re: 比熱
nibbana さんのレス (2007/06/20(Wed) 18:05)
>クロメルさん その議論,「なるほど!」,と思ったのですが, ひとつ意見を.
Nが十分大きいとして,エネルギー等分配の法則から(N個の調和振動子として),
E = kTN
よって,
dE/dT = kN
Mが十分大きいところ = δが十分小さいところ = エネルギーが連続の極限 では一定値 kN に収束するのでは.
Re: 比熱
nomercy さんのレス (2007/06/20(Wed) 18:30)
確かに調和振動子や自由粒子系といった簡単な(計算できる)系では具体的に比熱を計算して,それが絶対零度で零になることは確認できるでしょう. 他にももっと複雑な系において,現在までに計算された,あるいは実験で測定された比熱は絶対零度で零になっているように振る舞っています. 逆に言えばこの性質はそういった意味で経験的にしか示されていないのではないでしょうか? つまり普遍的に成り立つ性質なのかどうか?
Re: 比熱
yama さんのレス (2007/06/21(Thu) 00:03)
純粋な古典統計では,熱力学の第3法則(ネルンストの定理)を導くことはできず,従って絶対零度で比熱が 0 になることも導けません.これらは量子統計によって導かれるものです. このことは,ランダウ-リフシッツ「統計物理学」に明確に記述されているので,その部分を引用しておきます.
それゆえ,次のような重要な結論が得られる.すなわち,あらゆる物体のエントロピーは絶対0度において 0 になる(いわゆるネルンストの定理).
この定理は,とびとびの量子状態という概念が本質的な役割を果たしている量子統計の帰結であることをとくに注意しておこう.この定理はエントロピーが一般に任意の付加定数だけ不定である純古典統計においては証明することができないのである.
ネルンストの定理によって 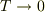 における二三の他の熱力学的量の様子についても結論を下すことができる.
たとえば
における二三の他の熱力学的量の様子についても結論を下すことができる.
たとえば 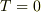 においては熱容量
においては熱容量 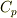 も
も 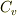 もともに 0 になることが容易にわかる.
もともに 0 になることが容易にわかる.
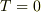 において
において 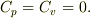 このことは次の形に書かれた熱容量の定義から直接みちびかれる.
このことは次の形に書かれた熱容量の定義から直接みちびかれる.
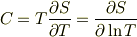
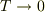 のとき,
のとき, 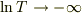 であるから,
であるから,  は一定の極限(0)に近づこうとするので,上の微分が0に近づくことは明らかである.
は一定の極限(0)に近づこうとするので,上の微分が0に近づくことは明らかである.
Re: 比熱
nomercy さんのレス (2007/06/21(Thu) 01:36)
yamaさん
ランダウ=リフシッツは熱力学第三法則は証明できるという立場をとっているんですかあ.他の本だと「第三法則は経験則だ」と言っているものもありますね.清水明著「熱力学」とか.
ランダウ=リフシッツでは 「任意の系で,基底状態に縮退は無い」 ということから第三法則を結論しているかと思いますが, この点は少し考えどころだと感じます. というのは模型によっては基底状態に巨視的な数の縮退が生じる場合があるからです. (一番有名な例では強磁性Heisenberg模型でしょうか)
ただし,所詮は模型であって現実の系では模型で記述しきれない微小な相互作用や外場が存在するはずだから,それによって縮退は解かれて基底状態は縮退していない, よって第三法則が成り立つ という考えもあるかと思います.
と,だんだんと訳が分からなくなってきそうなので, とりあえず
「"普通は"第三法則が成り立つ」 →「No.16506の議論により比熱は絶対零度で零になる」
ぐらいに思っておくのが平和的ですね.
Re: 比熱
nibbana さんのレス (2007/06/21(Thu) 11:10)
この種のことについてはもちろん本にいろいろ書いてあるでしょう. とはいえ,具体的な場合について自分なりに計算するのは意味のあることです.
>クロメルさん
・クロメルさんの計算に対する私の指摘について: -> 考え方そのものの問題では無く,極限の計算をミスってないでしょうか?
・あくまで古典統計であることについて: ->もちろん低温の極限では系のエネルギーが小さいわけですから,エネルギー準位 が離散的であることは無視するわけにはいきません.量子論的に扱う必要があるのは 当然です. ,,,ところでクロメルさんの計算ではエネルギーを離散的にあつかっています. 実質的にはほとんど量子系では,,と思うわけですか?
ここに結果を書くかどうかはともかく. 量子統計として計算してみては.具体形な系で比熱がどうなっているか, 何故そうなのかを確かめておけば, その他の場合(例外的な場合?)についても直観的な理解を得易いかもしれませんから.
以上が私の意見です. 後はお好きに.
Re: 比熱
yama さんのレス (2007/06/21(Thu) 17:17)
クロメルさんの計算結果は,比熱をMの関数として(従ってエネルギーの関数として)表しているわけですが,これでは比熱が温度によってどのように変化するのかわかりにくいですね. 温度の関数として表したほうがいいと思います.
Re: 比熱
クロメル さんのレス (2007/06/21(Thu) 21:07)
>nomercyさん なんだか一般性を意識して考えたつもりだったのですが,僕の計算はあくまで僕の取ったモデルではという限定された話のようですね(^^;)なるほど,縮退があることなんかも考えなければならないですね.複雑な系は本当に複雑そうです.
>yamaさん
第三法則の証明のところで,Sが一定値にちかづくから,微分はゼロになるという話の持っていき方のようですが,その近付き方が問題になるのではないですか?ちょっと明らかではないように思えるのですが….あと,MではなくTの関数にするのは,後で(だいぶ後になりそうですが)やってみようと思います.
>nibbanaさん
そうですね.確かに高温極限で固体の比熱は一定であるというデュロンプティの法則のようになるはずですね.考えてみたのですが,僕のモデルでは各々の振動子がとるエネルギーが本当は大きくなるにしたがって確率が少なくならなければならないのに,そうなっていないのが原因かと思います.おそらく,一つの振動子がエネルギーの塊を幾つ持っていても等確率として扱ってしまっている気がします.エネルギーがゼロか一つかという低温極限としてはそれなりに妥当なのかなと思っています.あと,振動子の取るエネルギーが離散化されていますので,量子統計の簡単なモデルのつもりでした.ひとつはっきりさせたいのは,あくまで離散化されているのは,振動子のエネルギー準位であって,エネルギー自体は連続的なものだと思っています.
Re: 比熱
クロメル さんのレス (2007/06/21(Thu) 22:13)
比熱を温度で表すように,計算してみました.
基本となる式は,
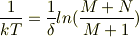
です.
Mについて解くと,
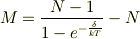
ですから,
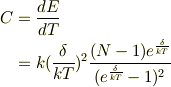
固体物理の教科書にでてくる様な式になりましたね.正にデュロンプティの法則です.
高温極限では 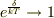 となり,これと指数関数を一次まで展開してやれば,
となり,これと指数関数を一次まで展開してやれば, 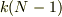 に収束します.
思うんですけど,これって
に収束します.
思うんですけど,これって 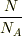 (
( 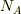 はアボガドロ数)で割るべきですよね.エネルギーをモル数で割らなければ,モル比熱とはいえません.割らないと熱容量だと思います.教科書にも比熱って書いてあるし….
はアボガドロ数)で割るべきですよね.エネルギーをモル数で割らなければ,モル比熱とはいえません.割らないと熱容量だと思います.教科書にも比熱って書いてあるし….
Re: 比熱
yama さんのレス (2007/06/21(Thu) 23:46)
クロメルさんのモデル計算はアインシュタインの比熱の理論と同等なものだと思いますが,このモデルでは確かに T→0 のとき C→0 になることが分かりますね.
一般の場合ですが,Sが0に近づく近づき方は lnT が-∞に向かうとき,Sは単調に減少して0に漸近するので,lnTを横軸 ,Sを縦軸にとったグラフを考えると,グラフの接線の傾きすなわち熱容量は lnT→-∞ の極限で0になるといえると思います.
Re: 比熱
クロメル さんのレス (2007/07/06(Fri) 00:47)
すいませんyamaさん,返信遅れました.
>一般の場合ですが,Sが0に近づく近づき方は lnT が-∞に向かうとき,Sは単調に減少して0に漸近するので,lnTを横軸 ,Sを縦軸にとったグラフを考えると,グラフの接線の傾きすなわち熱容量は lnT→-∞ の極限で0になるといえると思います.
なるほど,SはlnTに比例するような,よっぽど激しい減少をしない限り,零になるんですね.ありがとうございました.
Re: 比熱
クロメル さんのレス (2007/07/28(Sat) 23:13)
追加レポートです.今日勉強していたら,この話に関連した話が書いてありました.
僕の扱ったモデルは,古典論の話のようです. 量子論を導入した場合,十分低温では温度を上げても振動子を励起できない領域があり,そこでの比熱は0となると書いてありました.
振動子を励起できるほど,高温になると比熱は,古典論で求まる 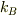 と一致するようになるそうです.
と一致するようになるそうです.
Re: 比熱
nomercy さんのレス (2007/07/29(Sun) 20:17)
クロメルさん
それって No.16532 と同じではないのですか? No.16532の結果はいわゆるアインシュタイン比熱の式で, 量子性は取り入れられてると思いますよ.
Re: 比熱
クロメル さんのレス (2007/07/30(Mon) 00:50)
>nomercyさん
そうなのですか. この式を導出する際に代入に使ったのは,温度の定義式,
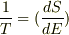
(この式自体は,古典論と量子論で共通のはず)を古典論の近似で書いたものだったのです.つまり,
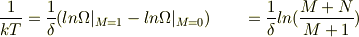
(  は状態数)という式でした.
は状態数)という式でした.
この式の問題点は,微分ではなく,差分を使っているところです. この式では,最低温度が非零の有限値であり,その値以下の温度が 定義できないところにあります. それを,代入によってMを消し去り,あたかもT=Oの温度が定義できているかのように,T→0としてしまった所が,僕としては気持ち悪かったです.
僕が読んだ量子統計の話では,振動子を励起できない温度領域もあるような書き方がされていました.そういう領域が存在すれば,温度のエネルギーを増大させても励起は起こらず,<E>が変わらないため,比熱は0なのだそうです. そうなると,問題は振動子を励起できない温度を,どうやって決めるかですね.これについては,書かれていませんでした.
比熱が0であることを示すには,振動子の励起に必要なエネルギー 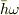 が小さい振動子系を熱浴とし,
が小さい振動子系を熱浴とし, 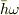 が大きな振動子系を囲えばいいのでしょうか?
が大きな振動子系を囲えばいいのでしょうか?
あんまり解決になってませんでしたね.すみませんでした.
Re: 比熱
nomercy さんのレス (2007/07/30(Mon) 04:18)
クロメルさん
差分としたのが気持ち悪いとのことですが, しかし差分と考えざるを得ませんよね. (エネルギーが完全に離散的なら本当の意味での微分は存在しませんしね) M,Nが非常に大きいことから差分と微分はほとんど同じである と考えれば良いのでは?
>僕が読んだ量子統計の話では,振動子を励起できない温度領域もあるような書き方がされていました.そういう領域が存在すれば,温度のエネルギーを増大させても励起は起こらず,<E>が変わらないため,比熱は0なのだそうです.
厳密に0ではなくて,比熱が非常に小さい,ということですよね? その振る舞いは No.16532 の式にも出ていると思いますよ. δ以下の温度領域で温度を下げていくと指数的に比熱が小さくなります.
Re: 比熱
zoro さんのレス (2007/07/30(Mon) 09:32)
クロメルさん,
物理の論議に関係ない話ですが,
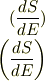
とすると,後者が見易いと思います.多分,時間がなかったのだろうと思いますが.
ちなみに,原稿は, <Tex> ( frac{dS}{dE} )\ left( frac{dS}{dE} right) </Tex>
LaTeX使いになるのを躊躇されている方々の為にコメントさせて戴きました.
〜〜〜 ついでにTIPSですが,日本語登録で;
「かか」→left( right) 「ああ」→<Tex></Tex> 「うう」→frac{}{}
としています.以上,お邪魔様でした.
Re: 比熱
クロメル さんのレス (2007/08/01(Wed) 01:38)
>nomercyさん そうですね.そうかんがえることにします.
でも一つだけ. 指数関数的減少は,絶対零度においてゼロになる言った方がいいはずと思います. でないと,エントロピーが発散してしまいます.
つまり,
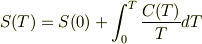
において,T→0で,右辺第二項の広義積分は,発散します.
>zoroさん
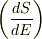
ですね.覚えておきます.
Re: 比熱
nomercy さんのレス (2007/08/01(Wed) 02:13)
クロメルさん
>でも一つだけ. >指数関数的減少は,絶対零度においてゼロになる言った方がいいはずと思います. >でないと,エントロピーが発散してしまいます.
ここの意図が良く分からないですが, No.16532の結果はNo.16537で言われたように T→0でC→0になりますよね?問題ないのでは?
Re: 比熱
クロメル さんのレス (2007/08/01(Wed) 07:52)
>nomercyさん
はい,そのようです.
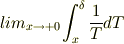
が,無限になってしまうということをいいたかったのですが,
ここで被積分関数に指数関数倍 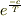 を掛けると,収束するので問題無しです.
を掛けると,収束するので問題無しです.
Re: 比熱
nibbana さんのレス (2007/08/01(Wed) 18:38)
小正準集合を使ったからといって古典論だとなるわけもなく, 振動子のエネルギーを離散的なものとしているので本質的に量子系と同じはずだと 思うのですが, 微分を差分におきかえざるを得ないところをどうしたものか,, と考えて,結局,Nが十分大きいとしてスターリングの公式を使ってみたものの処理できない項が残りどうしたものやら.
で,多少手もちの本で調べてみると,久保の大学演習に,同じ系を同様に扱っている 問題がありました.$5.16の例題 3 です. ここではM,Nどちらも十分大としてスターリングの公式を使用していました.
議論の参考にどうぞ.
Re: 比熱
nibbana さんのレス (2007/08/01(Wed) 18:42)
追伸;
,,,確かに振動子の数Nが十分大きいならば,零度近くであってもMが十分大として良いのでしょうね.(エネルギーは示量変数! 系が大きければエネルギーも大!)
Re: 比熱
クロメル さんのレス (2007/08/02(Thu) 05:32)
>nibbanaさん
なるほど,参考になります. 確かに僕が今まで考えていた領域は,現実には到達できないくらいのM〜1(個)という低温ですよね.これだけ低温だと,いろんな量が平均からのゆらぎなんかも無視できないほど大きくなり,物理量が定義できなくなるなぁと思いました.