一般化運動量の物理的意味
一般化運動量の物理的意味
けん(大学2年) さんの書込 (2007/06/16(Sat) 01:42)
x方向に水平運動している質量m1の質点が支点になっている,質量m2,長さlの単振子を考える.鉛直下方には一様重力加速度gが作用している.
質点m1の位置については,x1=Xと書く(z1=0).Xと単振子の角度座標θとする. m2の位置は, x2=X+lsinθ z2=-lcosθ となる. ラグランジアンLは, L=((m1+m2)/2)(dX/dt)^2+(m2/2)((l^2)(dθ/dt)^2+2l(dX/dt)(dθ/dt)cosθ)m2glcosθ となります. 共役な一般化運動量 px=(m1+m2)(dX/dt)+(m2)l(dθ/dt)cosθ =(m1)(dx1/dt)+(m2)(dx2/dt) pθ=(m2)(l^2)(dθ/dt)+(m2)l(dX/dt)cosθ となります. pxは2質点の全運動量のx方向成分を表します. では,pθは何を表すのでしょうか? よろしくお願いします.
Re: 一般化運動量の物理的意味
yama さんのレス (2007/06/17(Sun) 21:10)
計算してみれば分かると思いますが,pθは考えている瞬間の支点のまわりの角運動量になります. つまり,考えている瞬間に原点が支点と一致しているような静止座標系を考えると,その原点のまわりの角運動量がpθになるわけです. (支点に固定されて支点とともに動くような座標系を考えるわけではありません.)
Re: 一般化運動量の物理的意味
けん(大学2年) さんのレス (2007/06/18(Mon) 18:10)
レスありがとうございます. (m2)(l^2)(dθ/dt)は支点,つまり質点m1の周りの角運動量だとは分かるのですが, (m2)l(dX/dt)cosθは何なのでしょうか. それとも,(m2)(l^2)(dθ/dt)+(m2)l(dX/dt)cosθがm1の周りの角運動量だということでしょうか?
Re: 一般化運動量の物理的意味
yama さんのレス (2007/06/18(Mon) 23:50)
支点とともに動く座標系では,支点のまわりの角運動量が (m2)(l^2)(dθ/dt) になります. しかし,静止している座標系では,質点m1の速度は,支点に対する速度に支点の速度を加えたものになるので,後者に起因する角運動量 (m2)l(dX/dt)cosθ が加わることになります.
Re: 一般化運動量の物理的意味
けん(大学2年) さんのレス (2007/06/23(Sat) 00:06)
>静止している座標系では,質点m1の速度は,支点に対する速度に支点の速度を加えたものになるので,後者に起因する角運動量 (m2)l(dX/dt)cosθ が加わることになります.
考えてみたのですが,すみませんが,よく分かりません.もう少し詳しく教えて頂けないでしょうか.
Re: 一般化運動量の物理的意味
yama さんのレス (2007/06/23(Sat) 23:50)
静止座標系Kでの質点m1の座標を  とすると,原点のまわりの角運動量は
とすると,原点のまわりの角運動量は 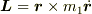 です.
支点が速度
です.
支点が速度 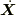 で動いているとき,この速度で動く座標系K'での質点m1の座標を
で動いているとき,この速度で動く座標系K'での質点m1の座標を 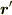 とすると,その原点のまわりの質点m1の角運動量は
とすると,その原点のまわりの質点m1の角運動量は 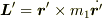 です.
です.
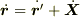 の関係があるので
の関係があるので
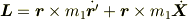
となりますが,考えている瞬間にK系とK'系の原点が一致したとすると,そのとき 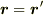 となるので
となるので
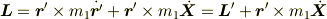
となり,具体的に計算すると 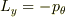 となります.
となります.