ガウスの法則

zoroさんの言ったとおりに考えました．そして，その考え方により導線１からの電界と，導線２からの電界を求めました．その２つを足して，答えとして dλ/π 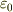${\varepsilon}_0$ ( d^2-x^2 ) のようになりました．回答としてはこれで正しいのでしょうか？また，zoroさんが「他の解法でもよいですが」といっていたように，他の解き方はどのような解き方なのでしょうか？

Re: ガウスの法則

zoro さんのレス (2007/06/10(Sun) 09:32)

もし，xがrを意味するなら違うと思います．

検算として， r=0を代入した時，導体1と導体2からの電場は「逆向きで・大きさは同じ」なので足し合わせるとキャンセルしてゼロになるずだからです．一般的に，静電場についてのガウスの面積分を使う問題は，色々な対称性を含んでいるので，検算にもその点を積極的に利用してくださいね．

他の解法は，導体の半径が規定されていないので，逆手にとって，半径→0の極限で，導体に沿ったz軸を考える事にします．すると，点Pを含むz軸に垂直面のz軸上の点をその原点をAとすれば，+/-zの点で，長さdzの部分の電荷が点Pに生じる電場がクーロンの法則で求まります．そして点Aに付いての対称性から，両者を足すと，A→Pの線分上の成分しかない事がわかります．あとは，線積分を実行するだけですね．

Re: ガウスの法則

KOO さんのレス (2007/06/10(Sun) 12:01)

なるほど，たしかにｒ＝０の時はE=０ですよね...... ってことは，２つの導線の間の電場は０になるってことですか？

もしくは，１：ｒ＝０の時２：０＜ｒ＜ｄの時３：ｄ＜ｒの時この３パターンに分けて，それぞれの電場を求めるってのは間違いですか？

Re: ガウスの法則

zoro さんのレス (2007/06/10(Sun) 12:29)

ああ，場合分けっていうのは面倒ですね．出題者さんのトラップに引っかかりました(泣)．

1,2は一緒で良いと思います．電場の符号が反転しますね．3の場合は，符号は反転しません．

Re: ガウスの法則

KOO さんのレス (2007/06/10(Sun) 13:07)

１，２は一緒でいいってことは，ｒ＝０の時にE=０だから，２のときもE=0になるってことですか？

また，符号が反転するというは，０＜ｒ＜ｄの場合でも導線１側にとった点Pと導線２側にとった点Pとで，電場の向きが変わるって事ですか？そうすると，３の時も導線１より左側の場合と，導線２より右側の場合で電場の向きが変わると思うのですが....... これは私の勘違いでしょうか？？

Re: ガウスの法則

zoro さんのレス (2007/06/10(Sun) 15:15)

以前書いた絵で，導線１から導線２に向かった軸をかんがえ，その方向に向いた場合を＋，その逆を向いたらーとします．また，導線１からR離れた時の電場強度を; E(R) = λ/(2πε0|R|) := k/|R| とします，そしてP点での電場EPとし，R1 :=d-r ，R2 := d+r，とすれば，

A) (+d > r >-d)or (-d < -r < d) : 軸1,2の間 EP = +E(R1) -E(R2) = +k/|d-r| -k/|d+r| = +k/(d-r) -k/(d+r) = +2rk/(d^2-r^2)；ここで，符号は中心を境に，左側で正，中央でゼロ，右側で負

B) (r > +d) : 軸1の左 EP = -E(R1) -E(R2) = -k/|d-r| -k/|d+r| ；ここで，0 > (d -r), (d+r) > +2d = -k/(r-d) -k/(r+d) = -2rk/(r^2-d^2) = +2rk/(d^2-r^2) ；ここで符号は負

C) ( -d > r) : 軸2の右 EP = +E(R1) +E(R2) = +k/|d-r| +k/|d+r| ；ここで, 2d < (d-r), (d+r) <0 = +k/(d-r) -k/(r+d) = +2rk/(d^2-r^2)；ここで符号は正

場合分けしたものの，最終形が同一なのは面白いですね．

こういう問題は，点電荷の問題で見た気がします．物理の問題というよりは，算数の問題ですね．考えてしまう．

Re: ガウスの法則

KOO さんのレス (2007/06/12(Tue) 00:35)

おかげさまで理解することができました．どうもありがとうございます．

[home] [掲示板] [ページの先頭]