aya さんの書込 (2007/06/07(Thu) 03:45)

初めまして，現在大学１年です． 物理は全くの初心者です;

ｘ軸上を物体が運動している． 時刻ｔ＝１に物体は，位置ｘ＝１/３を速度ｖ＝１で通過した． 物体の速度がａ(ｔ)＝２ｔ−４であるとき，時刻ｔの物体の速度ｖ，位置ｘを求めよ．

ａ(t)=2t-4 v(t)=∫a(t)dt =f(t)+c_1 v(1)=f(1)+c_1=1

x(t)=∫v(t)dt =h(t)+c_2 x(1)=h(1)+c_2=3/1

までは考えられたのですがこの後がどうしても分りません． 解き方を教えて頂けないでしょうか？

zoro さんのレス (2007/06/07(Thu) 08:32)

ayaさん，初めまして．

この問題は，「運動の式が与えられてなくて，その代わりに，加速度が時間の関数として与えられているのだ」と思います．ですから，力を計算出来ません．その代わりに，加速度からの時間積分をして速度を，さらに速度の時間積分をして距離を求めるだけですね．

以下，積分の範囲を使うので，数式表示モード(簡易LaTeX)を使います．

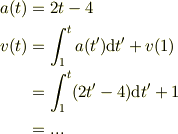
として，積分を実際に行ってみたらどうでしょうか．後も同様にできませんか？

もし，上の式を普通の文字で書くとすれば；

v(t) = ∫_1^t a(t')dt' +v(1)

= ∫_1^t (2t' - 4)dt' +1

とかですかね．

ちなみに，簡易LaTeXでは， <Tex> a(t) &= 2t-4\ v(t) &= int_{1}^{t}a(t')mbox{d}t' +v(1)\ &= int_{1}^{t}(2t'-4)mbox{d}t' +1\ &= ... </Tex> と書いています．実際には<Tex>,</Tex>の「T」→「t」にする必要があります．