微分方程式
微分方程式
tip★ さんの書込 (2007/06/05(Tue) 20:04)
教科書の答えに間違いがあるかと思っているのですが,自信がないのでどなたか次の問題よろしくお願いします.
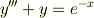
なんですが, 非同次方程式の特殊解が
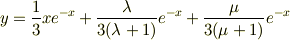
ただし
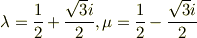
ここまで自分で解きました.
教科書の答えでは, 元の微分方程式の一般解が,
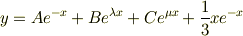
となっているのですが,どうしてもこのようになりません.どこが間違っているでしょうか?
Re: 微分方程式
toorisugari no Hiro さんのレス (2007/06/05(Tue) 20:27)
> 非同次方程式の特殊解が >
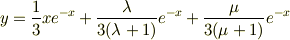
これ,特殊解なら右辺第1項だけで十分とおもいます.(第2項,第3項は同次方程式の一般解に含まれますから).
> 元の微分方程式の一般解が,
「非同次方程式の一般解が」ですね.
非同次項( 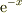 )を抜いた同次方程式
)を抜いた同次方程式
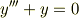
の一般解はわかるのですよね?
Re: 微分方程式
tip★ さんのレス (2007/06/05(Tue) 20:57)
特殊解の第2項と第3項を合わせものが
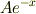
に含まれているということでいいですか?
>非同次項( 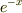 )を抜いた同次方程式
>
)を抜いた同次方程式
> 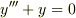 >の一般解はわかるのですよね?
>の一般解はわかるのですよね?
分かります.
Re: 微分方程式
tip★ さんのレス (2007/06/05(Tue) 21:01)
ありがとうございました
Re: 微分方程式
zoro さんのレス (2007/06/05(Tue) 21:16)
tip★さん,
線形の微分方程式に外部からのかく乱 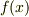 が入ったとして説明します.
が入ったとして説明します.
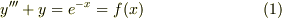
この方程式を任意の初期条件で解くには,外部かく乱が無いときの式;

微分方程式(1)の同次方程式と呼びますよね.今の場合,3次の微分方程式ですから,少なくとも3つの独立した解が在る筈で,恐らく,この解は得られたのだと思います.
これら同次方程式の独立な解を, 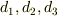 とすると,これらの任意の足し合も,式(2)の解であるとともに,式(1)の解に足してもやはり式(1)の解である訳です.(ブラボー)
とすると,これらの任意の足し合も,式(2)の解であるとともに,式(1)の解に足してもやはり式(1)の解である訳です.(ブラボー)
#私は 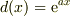 として
として  の方程式を解きました.
の方程式を解きました.
次に,本来の式(1)の解を求める事を考えます.
>非同次方程式の特殊解が
> 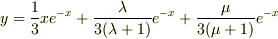
と書かれていますが,右辺第1項が特殊解だと思います.
普通,外部かく乱項がexpタイプの場合,特殊解を;
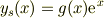
として,g(x)の微分方程式として,

みたいになりましたね.
とにかく式(3)は,解ければいいので,一番簡単な解を視察で求めます.
従って,求める解は;
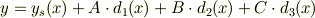
となるのだと,思います.
当たり前ですが, 特殊解は外部かく乱を表し, 同次方程式の係数は,初期条件に応じて決まりますね.
たまには,具体的な解を得てから,一般論を眺めるのも面白いですね.
追伸:
tip★さんの解だと,振動的な挙動が全然入り込みませんが?
Re: 微分方程式
山旅人 さんのレス (2007/06/05(Tue) 23:58)
> tip★さんの解だと,振動的な挙動が全然入り込みませんが? λ,μ が複素数ですから,e λx ,e μx に振動的挙動が入っています.λ=a+bi,e λx =e a (cosbx+isinbx)
Re: 微分方程式
zoro さんのレス (2007/06/06(Wed) 00:26)
山旅人さん,
>> tip★さんの解だと,振動的な挙動が全然入り込みませんが? >λ,μ が複素数ですから,eλx,eμx に振動的挙動が入っています.
でもそう書いてないですね.
そもそも; >特殊解の第2項と第3項を合わせものが
>A e^{-x}
>に含まれているということでいいですか?
と書かれているので心配になりました.
細かい話ですが,-1の三乗根ですから,解は3つですね.-1も立派にその一つと思いますが,なんで書かれないのですか?
〜〜〜 明日早いので,今日は寝ます.御免なさい.
Re: 微分方程式
tip★ さんのレス (2007/06/06(Wed) 20:46)
zoroさん
自分の教科書に書いてないものがちらほら・・・
教科書の例題を真似しながら解いたので,流れは一通りいいもんだと思っていました.
できたら模範解答を載せてほしいです.
Re: 微分方程式
zoro さんのレス (2007/06/06(Wed) 21:41)
>できたら模範解答を載せてほしいです.
前回書いた部分のどこが判らないかを書いて下さい.まず,そこをアタックして,また,その次を質問して下さると,回答し易そうです.
一度に書くと,間違いが多発する可能性がありますし....
Re: 微分方程式
tip★ さんのレス (2007/06/06(Wed) 23:09)
普通,外部かく乱項がexpタイプの場合,特殊解を;
として,g(x)の微分方程式として,
みたいになりましたね.
とにかく式(3)は,解ければいいので,一番簡単な解を視察で求めます.
の部分と(式は省略しています.)
細かい話ですが,-1の三乗根ですから,解は3つですね.-1も立派にその一つと思います
の部分がよくわかりません.
Re: 微分方程式
zoro さんのレス (2007/06/07(Thu) 00:45)
判りました,「-1の三乗根」と「expタイプの場合,特殊解」の順で説明します.なお,私は,数学が苦手で,計算間違いも多いので,ご自分でも検算の積もりで,計算をフォローして下さい.
■-1の三乗根:同次方程式の解として
線形微分方程式ので外部かく乱の無い場合;
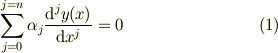
今の場合,係数 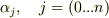 は常数とします.
は常数とします.
解を;

と仮定すれば, 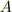 は代数方程式,
は代数方程式,

の解になります.この方程式の最大次数が  ですから,Aの解も
ですから,Aの解も  個になります.
個になります.
#同次方程式の積分常数の個数にも一致します.
このAの解の組; 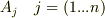 は,同次方程式の固有値で,解の組;
は,同次方程式の固有値で,解の組; 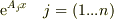 は,同次方程式の固有関数になります.
は,同次方程式の固有関数になります.
#この場合,方程式(3)の解が縮退のない(重根のない)ものに限定します. #縮退の在る場合については,専門書をご覧下さい.
今回の場合で言えば,toorisugari no Hiroさんが,始めにご指摘されたように;

ですから,固有値方程式としては;

なります.
これを説明しますが,その前に,Johさんの解説「1のn乗根」;
を見て下さい.式(5)は「-1のn乗根」なので少し違いますが,基本は同じです.また「n=3」について限定して考えます.
さて,
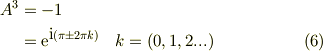
両辺の1/3乗をとれば,
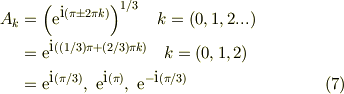
オイラーの公式で書き下せば,tip★さんの計算値 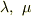 に「-1」を加えた,3つが固有値になります.
に「-1」を加えた,3つが固有値になります.
この固有値に対応して,固有関数を計算するには,山旅人さんの示されたようにするのも一法だとおもいます.
もし, 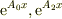 が複素数で嫌ならば,これらは相互に複素共役であるので,オイラーの公式を逆に用いて,新たな固有関数を;
が複素数で嫌ならば,これらは相互に複素共役であるので,オイラーの公式を逆に用いて,新たな固有関数を;
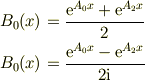
と線形変換をすればどうでしょうか.
Re: 微分方程式
なんとなく さんのレス (2007/06/07(Thu) 13:15)
なんとなくです. 質問と回答が噛み合っていないように見受けられますが,tip★さんの疑問点にはもっとストレートな回答で良いと思います.いくつかの点で混乱されているようですが,少し基本的なところから説明させて下さい. ちゃんとした説明は微分方程式論で学んで頂くとして,この問題で必要な基礎知識として,(線形微分方程式を思い浮かべてください) この微分方程式は3次である. (1)非同時(斉時)微分方程式の解は同時(右辺=0とした)方程式の一般解に非同時方程式の特殊解を加えたものが一般解となる. (2)同時方程式がn次線形微分方程式なら,n個の線形独立な解があり,一般解はその線形結合で書ける(縮退していない場合). (3)線形独立な解とは(一般に関数ですが)一方が他の(残りの)解の線形結合では書けないものであること(正確には線形代数で)を言う. (3)に関しては,e^(-x)とe^(-x+3)やAe^(-x)は独立ではないが,e^(-x)とe^(-2x)やxe^(-x)は線形独立.簡単に言えば定数倍+定数で互いに変換できるかどうかです.そうすると,tip★さんの最初の解の後ろ2つは独立でない関数を加えてみても,意味がないということです.なぜなら,微分方程式の(ある)解の線形結合はまた解となることは初めから分かっているからです. したがって,手順はまず同時方程式の一般解を求めることで,それはみなさんの書かれているようにすれば良いでしょう.ここで出てくる3関数((2)参照)はそれぞれ線形独立な解でなければなりません.指数部分を比較すれば分かりますね. つぎに非同時方程式の特殊解を求めますが,おそらくその一般的手順はありません.ケースバイケースですが,右辺が指数関数である場合,多項式×指数関数の形を想定することが多いようです.ここでは,Y=A(x)e^(-x)と置いて,非同時方程式に代入してみると, (A'''-3A''+3A')e^(-x)=e^(-x) となります.両辺を比較すれば,3A'=1,A=(1/3)xつまりy=xe^(-x)/3が特殊解であり,前記同時方程式の各解と線形独立な解であることが分かります. したがって,一般解は,tip★さんの教科書に書かれていた解となることが分かります.微分方程式の解の唯一性定理から,一般解が得られたことになります.
Re: 微分方程式
tip★ さんのレス (2007/06/08(Fri) 00:08)
zoroさん
解説ありがとうございます. 若干納得できない部分もありますが,自分で調べて解決したいと思います.
なんとなくさん
右辺が指数関数のとき多項式×指数関数の形を想定する・・・自分の教科書にはまったく載ってないないようです.他のほんでしらべてみようと思います.
Re: 微分方程式
toorisugari no Hiro さんのレス (2007/06/08(Fri) 00:25)
> 右辺が指数関数のとき多項式×指数関数の形を想定する・・・自分の教科書にはまったく載ってないないようです.
もっと簡単な問題,たとえば
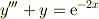
なら, 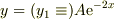 を上式に代入して未定の定数
を上式に代入して未定の定数 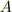 を決定(
を決定( 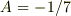 )すればよいのです.これで特殊解
)すればよいのです.これで特殊解 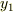 が得られたので,同次方程式の一般解
が得られたので,同次方程式の一般解 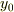 と足し合わせれば,目的は達成できます.
と足し合わせれば,目的は達成できます.
しかし,懸案の問題
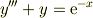
は,違います.非同次項 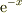 が同次方程式
が同次方程式
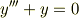
の解になっています.これを共鳴(音叉の共鳴の「共鳴」です.)問題といいます.
この場合,従来の方法に従って 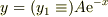 を代入しても
を代入しても 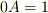 と不能になってしまいます.
と不能になってしまいます.
そこで,定数変化法という方法を行います.これは「定数( 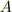 )を関数(
)を関数( 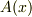 )に置き換えなさい.」という簡単なルールです.微分方程式の教科書にも必ず載っています.
)に置き換えなさい.」という簡単なルールです.微分方程式の教科書にも必ず載っています.
Re: 微分方程式
zoro さんのレス (2007/06/08(Fri) 07:06)
tip★さん,
>若干納得できない部分もありますが,自分で調べて解決したいと思います.
自己解決を目指すのには賛成です.できれば,解決できたと思ったときに,回答をここに書き込んでもらえたら嬉しいです.
#他人に説明するのが,最良の勉強法です,キッパリ.
もちろん,検討中に,判らないところにぶつかったら,気軽に質問してください.
この問題は,ある意味でとてもよい問題だと思います.その上,自分で作った解と,回答との違いを見逃さなかったtip★さんの眼力は凄いと思います.
私も,常微分方程式の問題に久しぶりにぶつかりました.処方箋はおぼろげに分かるのですが,3乗根の解の出仕方でオタオタし(Johさんの記事を思い出したので,助かりましたが),定数変化法という名前(toorisugari no Hiro さんの指摘で思い出しました)がでてこなかったりと,その他にも自分の説明力が萎えたと思い知りました.当面,この説明力を修復しようと思いました(笑).
tip★さん,これから何十年と使うツールとしての物理数学を自分用にますます磨き上げられますように.
Re: 微分方程式
なんとなく さんのレス (2007/06/08(Fri) 11:00)
toorisugari no Hiroの仰るとおり,定数変化法であり,それ以上は蛇足なのですが一言だけ.微分方程式の解法は変数分離形を始め,色々テクニックがあります.定数変化法も万能ではなく,もとの微分方程式より(解くのが)難しい式になることも屡々です.基本を押さえられたら,練習問題を数こなし,感覚的な直観力を養うことは決して無駄にならないと思います.zoroさんも言われていますが,経験を積んで身に着ければ,強力なツールとなると思います.
Re: 微分方程式
ミュフ猫 さんのレス (2007/06/08(Fri) 11:11)
横レス失礼します. よく,数学公式集などに積分方程式(と言っても,y=の形ですが)の解が (原始関数の形で)載ってます. 微分方程式の解をまとめた専門書は無いのだろうか?
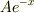 > に含まれているということでいいですか?
> に含まれているということでいいですか?