粒子の寿命

TERU さんの書込 (2007/06/03(Sun) 22:11)

はじめまして，現在大学3年のTERUと申します．

単純な問題なのですが計算段階でつまづいてしまっている問題があります．よろしければご教授お願いします．

(1)静止しているμ粒子は寿命2.2μ秒で電子と2つのニュートリノに崩壊する．運動量100MeV/cのμ粒子の寿命を求めよ．

静止系での粒子の経過時刻をt，粒子の運動する系での時刻をt'としてローレンツ変換してやれば，粒子の速度をv,β=v/cとすれば t=(1/√(1-β^2))t' の関係が得られる．寿命2.2μ秒をt'に代入すれば求める寿命は 2.2μ*(1/√(1-β^2)) と伸びる．

なのですがβ=v/cのところでつまづいております．今分かってるのは運動量なので運動量100Mev/cを質量で割ってやればvになると思うんですが質量が分からないからどうにも．．

よろしくお願いします．

TERUさん，始めまして．

本当は，出題者さんにお聞きになるべきとおもいます．静止質量は；

ぐらいを使えば，

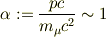
$\alpha := \frac{pc}{m_{\mu}c^2} \sim 1$

としてβを解いたら駄目でしょうか．

>今分かってるのは運動量なので運動量100Mev/cを質量で割ってやればvになると思うんですが

非相対論的な場合はそれでいいのですが，この問題は相対論的に考える必要があるので

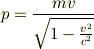
$p=\frac{mv}{\sqrt{1-\frac{v^2}{c^2}}}$

を用いて速度を求めなければならないと思います．