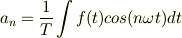フーリエ級数の問題

home > 掲示板 >

このページのPDF版

サイトマップ

フーリエ級数の問題

ココさんの書込 (2007/06/01(Fri) 23:30)

フーリエ級数の問題でつまづいています．

f(t)=-sinωt -T/2≦t≦0 f(t)=sinωt0≦t≦T/2 を利用してan,bnを求めよという問題です．

f(t)が偶関数なのでbnは0ですよね・・？ anなんですが，(sinωt)(cosnωt)の積分ができません．どうすればいいのでしょうか．

また，答えがわからないので，最終的に示すべき答えを教えていただけるとゴールが見えて嬉しいです；

テストが近くて焦っています(> <) よろしくおねがいします．

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/01(Fri) 23:37)

sin(ωt)cos(ωt)=1/2sin(2ωt)を使えばよさそうですね．

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/01(Fri) 23:42)

失礼しました． sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-cosAsinB より， sinAcosB=1/2(sin(A+B)+sin(A-B)) をつかってください．

この積分ができれば，答えはすぐ出ますよ．

Re: フーリエ級数の問題

ココさんのレス (2007/06/01(Fri) 23:48)

一応使って考えてはいるんですけど．．（> <）計算をすすめて，sin(ωt-nωt)dtの形が出るんですが，その積分ができなくて；

ちなみにa0＝2/Tω｛1-(-1)^n｝になったんですけど，おかしいですかね・・？

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/01(Fri) 23:55)

？…そんなに難しくないと思いますよ． ∫sin(1-n)ωt dt=-1/{(1-n)ω}cos(1-n)ωt +C =1/{(n-1)ω}cos(n-1)ωt +C(Cは積分定数)だと思いますよ．

答えはちょっと待ってください．

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/02(Sat) 00:25)

Tω＝２πですよね．

だとしたら，ｎが偶数のとき，

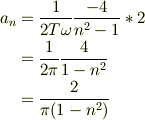
$a_n &= \frac{1}{2T\omega}\frac{-4}{n^2-1}*2 \\&= \frac{1}{2\pi}\frac{4}{1-n^2} \\&= \frac{2}{\pi (1-n^2)}$

だと思いますよ．ｎが０ならココさんと２倍の違いがあるようです． -T/2<t<0のときを考えて，２倍しましたか？

ｎが奇数なら，０のようです．

Re: フーリエ級数の問題

ココさんのレス (2007/06/02(Sat) 00:27)

あぁ！ほんとですね！どうもすいません； ∫sin(1-n)ωt dt=-1/{(1-n)ω}cos(1-n)ωt +C の分母は{(1-n)ω}でいいんですよね？

なんだか低レベルな質問ばかりで申し訳ないのですがマイナスをはずしたら（）のなかは両方とも(n-1)になるんですか？

答えまで考えていただいてありがとうございます．よろしくお願いします．

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/02(Sat) 00:33)

分母はその通りです．

両方っていうのは，どの二つかよくわからないんですけど，どれですか？

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/02(Sat) 00:46)

すいません，そろそろ寝たいので続きは明日にしましょう．

Re: フーリエ級数の問題

ココさんのレス (2007/06/02(Sat) 09:01)

遅くまで考えていただき，ありがとうございます．

0≦t≦T/2 で考えて2倍しているのですが，どうしても4/{π(1-n^2)}になってしまいます；しかもnが偶数のときが0で奇数のときがこれです．

何か考え方が違うのでしょうか・・；

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/02(Sat) 20:00)

すいません，つまらないことで悩ませてしまったかもしれません．僕は計算するとき

$a_n=\frac{1}{T}\int f(t) cos(n \omega t) dt$

としましたが，これって違いましたっけ？

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/02(Sat) 20:06)

偶数か奇数かですが，

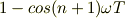
$1-cos(n+1)\omega T$

と言う式がでてきますよね． nが偶数なら，n+1が奇数で，コサインの項が-(-1)=+1 となり，残るのではないですか？

これについては，私が正しいと思います．なぜなら，n=0は偶数ですよね． a_0というのはいわば関数の平均値なので，この関数の場合，明らかに０ではないですよね．

Re: フーリエ級数の問題

ココさんのレス (2007/06/02(Sat) 22:56)

anの式は2/T〜で習いました．

えっと，積分した結果[cos(n+1)ωt](0≦t≦T/2) がでるんですけど，このtにT/2と0を代入した結果はどぉなればいいのでしょうか．．？多分そこで間違えてると思うんです(> <)

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/02(Sat) 23:40)

すいません，この場合考えている区間の長さがLなので，（−TからTを考えるときは2/(2T)=1/T〜なんですよ．これを私がごっちゃに考えていました．）2/T〜でした． No.16153の数式も訂正します．正しくは，

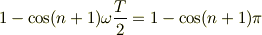
$1- \cos(n+1)\omega \frac{T}{2}=1- \cos(n+1) \pi$

でした．

本題ですが，

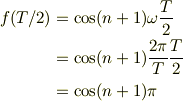
$f(T/2)&=\cos(n+1)\omega \frac{T}{2} \\&=\cos(n+1)\frac{2 \pi}{T} \frac{T}{2} \\&=\cos(n+1)\pi$

一方，

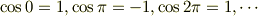
$\cos 0 = 1 , \cos \pi = -1 , \cos 2 \pi =1, \cdots$

つまり，(n+1)が偶数なら1，nが奇数なら1です．

また，

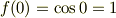
$f(0)=\cos 0=1$

です．

でてくるのは，

$&\ [ -\cos(n+1)\omega t ]^{T/2}_0 \\&= [\cos(n+1)\omega t]^0_{T/2} \\&= \cos 0 - \cos(n+1)\pi&= 1 -\cos(n+1)\pi$

です．nが奇数なら 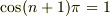$\cos(n+1)\pi=1$ ですから，このとき消しあって０になります．

Re: フーリエ級数の問題

ココさんのレス (2007/06/03(Sun) 20:10)

いろいろありがとうございます！！

またゆっくり（テスト前日になりそうですが・・）考えてみます．

本当にお世話になりました(*_ _)

Re: フーリエ級数の問題

クロメルさんのレス (2007/06/03(Sun) 20:51)

いえいえ，どういたしまして．

フーリエ級数は，積分がややこしいですよね．（nが一つではないので場合分けしなければならない）

テスト頑張って下さい．

[home] [掲示板] [ページの先頭]