二階テンソルの勾配
二階テンソルの勾配
koredeiina さんの書込 (2007/05/29(Tue) 20:18)
工学系博士課程学生です.恥ずかしながら数学に弱いのでご質問させて頂きます. 参考書,ネット等調べたのですがどうしてもはっきりとしたことがわかりません.
あるベクトルBの勾配∇Bを定義します.これは3×3行列の2階テンソルとなります.これに対して別のベクトルAとの内積を取り,(0,0,0)となりました場合,「ベクトルAと∇Bは直交している」と言うことが出来るのでしょうか?テンソルに対して直交と云うのも直感的には分かりづらいですが,定義としては成立するかと思います.ただ,数式展開上どうなのかと思いました
Re: 二階テンソルの勾配
toorisugari no Hiro さんのレス (2007/05/29(Tue) 20:31)
> あるベクトルBの勾配∇Bを定義します.これは3×3行列の2階テンソルとなります.これに対して別のベクトルAとの内積を取り,
添え字で表現したとき,この内積は
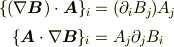
のどちらですか?たぶん後者かな?
> (0,0,0)となりました場合,「ベクトルAと∇Bは直交している」と言うことが出来るのでしょうか?
直交の意味がわかりませんね.
後者なら 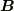 の
の 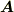 方向微分が0という意味づけができなくはないですが...
方向微分が0という意味づけができなくはないですが...
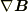 を反対称化した
を反対称化した ![[\nabla\bm{B}]_{ij}(=\partial_i B_j - \partial_j B_i)](http://hooktail.maxwell.jp/bbslog/ce9ae696a8752d75736114b48932c664.png) なら,「ベクトルAと[∇B]は直交している」とは前後関係なく「ベクトル
なら,「ベクトルAと[∇B]は直交している」とは前後関係なく「ベクトル 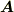 と
と 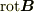 が平行なこと」とむりやり意味づけできますが,これも....
が平行なこと」とむりやり意味づけできますが,これも....
Re: 二階テンソルの勾配
Joh さんのレス (2007/05/29(Tue) 21:02)
一般に直交というのは,内積空間で独立な基底になるという意味だと思います.ベクトルと二階のテンソルを,一つのベクトル空間の基底としてごっちゃにしたものを見たことがないので,よく分かりません.(直和空間みたいなものを考えるのかなぁ)一度,内積とベクトル空間の定義に戻って,検証してみてください.それで内積がwell-definedなら,直交と呼んでもいいんでしょう.私には,あまりパッとしたイメージは湧きません.
Re: 二階テンソルの勾配
koredeiina さんのレス (2007/05/29(Tue) 21:59)
Joh様通りすがりのhiro様
迅速なご返信を有難う御座います.
具体的にどういう空間か,とのことですが,対象としている問題は3次元空間における電磁気の問題で,磁力線ベクトルの勾配と電流ベクトルが直交するかどうか,と云うものです.そもそも磁力線ベクトルの勾配と云う概念がベクトルにならないのでわかりづらいのですが,敢えて考えるとすれば 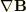 と云う2階テンソルで表記されるかと思いました.
と云う2階テンソルで表記されるかと思いました.
マクスウェル方程式の(変位電流項除く)
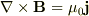 において両辺に後ろから
において両辺に後ろから 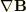 との内積を取りますと,私の考えている状況下においては各成分を計算した後,左辺の全ての成分が[0 0 0]となります.これで磁力線ベクトルの勾配と電流ベクトルは直交する,と云うことにならないか,(即ち
との内積を取りますと,私の考えている状況下においては各成分を計算した後,左辺の全ての成分が[0 0 0]となります.これで磁力線ベクトルの勾配と電流ベクトルは直交する,と云うことにならないか,(即ち 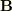 の等高線がそのまま電流ベクトルと云うこと)を端的に証明することにならないか,ということです.Bとjが直交していることはいわずもがなです.
の等高線がそのまま電流ベクトルと云うこと)を端的に証明することにならないか,ということです.Bとjが直交していることはいわずもがなです.
2階テンソルである 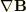 は平面を表していると思えます.
もしかするとどこかでアホなことを云っているかもしれませんが,こういう状況で実際に3次元空間における直交性を考えている次第です.
は平面を表していると思えます.
もしかするとどこかでアホなことを云っているかもしれませんが,こういう状況で実際に3次元空間における直交性を考えている次第です.
Joh様が仰る通り,テンソルとベクトルの内積がwell-definedであることを確認し,その内積が[0 0 0]になった,だから直交,と言うのが唯一にしてストレートな答えなのですが,well-definedかどうかがどこを調べても分かりません...
Re: 二階テンソルの勾配
Joh さんのレス (2007/05/29(Tue) 22:08)
一般的な内積の定義は,たとえば
を見てください.手前味噌ですが. 普通の線形代数の教科書なら,絶対出ていると思います.
ベクトルと行列の普通の積を考えるのだと,対称性, 正定値性もないと思いますし,線形性を考えるにはベクトルとテンソル の和というものを考えないといけませんが,これもよく分かりません. とりあえず,いま考えている積が,ベクトル空間の内積とは呼べない以上, その結果が0になったからと言って,それを直交と呼ぶことも出来ない ような気がします.
Re: 二階テンソルの勾配
toorisugari no Hiro さんのレス (2007/05/29(Tue) 22:49)
気になったので念のため.
> Bとjが直交していることはいわずもがなです.
一般に 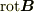 と
と 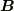 は直交しませんが,今回は直交する特別な場合なのですか?
は直交しませんが,今回は直交する特別な場合なのですか?
Re: 二階テンソルの勾配
koredeiina さんのレス (2007/05/30(Wed) 00:01)
Joh様通りすがりのhiro様
ベクトルとテンソルということで内積としての成立性が怪しいとのこと.リンク先も読みましたが確かにそんな気がするのでこれ以上勝手な定義を作るのはやめておきます.ただ,ベクトルと2階テンソルの内積(のような)計算というのは成立するようですので(マグロウヒル大学演習ベクトル解析92〜93p参照),それがゼロだと直交なのかなと思いました.実際,磁場の勾配と電流経路は電磁流体中で直交するらしいので,それの端的な表現(座標によらない)が出来ないかなと思ったのですが
>rotBとBは直交していない
はご尤もです.私の勘違いでした.ありがとうございます.
Re: 二階テンソルの勾配
yama さんのレス (2007/05/30(Wed) 00:21)
テンソルとベクトルが直交すると言えるかどうかはともかくとして,幾何学的な意味を考えてみました.
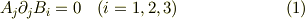
を 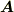 の成分についての連立方程式と考えると,0ベクトル以外の解を持つためには
の成分についての連立方程式と考えると,0ベクトル以外の解を持つためには

でないといけません.
この条件は,テンソル 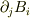 を3つの行ベクトル
を3つの行ベクトル
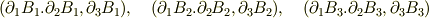
に分けて考えたとき,この3つのベクトルが同一平面上にあることを意味します.
そして(1)は, 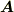 がこの平面に直交することを示しています.
がこの平面に直交することを示しています.
3次元空間の3つのベクトルに他のベクトルが直交するためには,3つのベクトルが同一平面上になければならないのは当然のことですね.
Re: 二階テンソルの勾配
zoro さんのレス (2007/05/31(Thu) 09:45)
横から失礼します.本来の質問とは別で申し訳ありません.
>3次元空間の3つのベクトルに他のベクトルが直交するためには,3つのベクトルが同一平面上になければならないのは当然のことですね.
素人目には,三つのベクトルの内,少なくともどれか2つのベクトルの方向が平行ないし反平行であれば,式(2)が成立するように思いますが....
Re: 二階テンソルの勾配
toorisugari no Hiro さんのレス (2007/05/31(Thu) 14:27)
> 三つのベクトルの内,少なくともどれか2つのベクトルの方向が平行ないし反平行であれば,式(2)が成立するように思いますが....
っ「必要条件と十分条件」
Re: 二階テンソルの勾配
zoro さんのレス (2007/05/31(Thu) 17:21)
>っ「必要条件と十分条件」
そうか,2つのベクトルの外積は,その両者で作る平面に垂直です.その外積ベクトルと3つめのベクトルの内積とがゼロなら,3つ目のベクトルは,少なくとも先の2ベクトルの作る平面に平行である事が言えるのでしょうね.
数学が弱いと,一体全体,どちらの方が制限が緩いのか?です.やはり物理的な状況が不明なままで,詳細な論議をしてもイメージが涌かないので,質問を取りさげます.失礼しました.